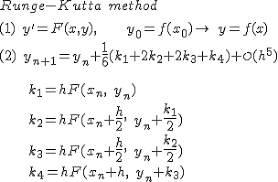Kelompok 13
Anggota Kelompok 13:
1. Viliasio Sirait
2. Muhammad Luqman Sugiyono
3. Zaim Kamil Muhammad
Pada pertemuan keempat, kami ditantang untuk membuat sebuah program python yang mampu menjawab eliminasi Gauss dari sebuh matriks. Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana. Caranya adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Eliminasi Gauss ini disempurnakan kembali dengan yang namanya Eliminasi Gauss Jordan. Dalam aljabar linear, eliminasi Gauss-Jordan adalah versi dari eliminasi Gauss. Pada metode eliminasi Gauss-Jordan kita membuat nol elemen-elemen di bawah maupun di atas diagonal utama suatu matriks. Hasilnya adalah matriks tereduksi yang berupa matriks diagonal satuan (semua elemen pada diagonal utama bernilai 1, elemen-elemen lainnya nol).
Berikut ini adalah kode program python yang telah saya pelajari:
from fractions import Fraction
def pprint(A):
n = len(A)
for i in range(0, n):
line = ""
for j in range(0, n+1):
line += str(A[i][j]) + "\t"
if j == n-1:
line += "| "
print(line)
print("")
# Performs and returns the gauss elimination
# @A : matrix
def gauss(A):
n = len(A)
for i in range(0, n):
# Search for maximum in this column
maxE1 = abs(A[i][i])
maxRow = i
for k in range(i+1, n):
# compares rows, first row can't start with zero
if abs(A[k][i]) < maxE1 or maxE1 == 0:
maxE1 = abs(A[k][i])
maxRow = k
# Swap maximum row with current row (column by column)
for k in range(i, n+1):
tmp = A[maxRow][k]
A[maxRow][k] = A[i][k]
A[i][k] = tmp
# Make all rows below this one 0 in current column
for k in range(i+1, n):
c = -A[k][i]/A[i][i]
for j in range(i, n+1):
if i == j:
A[k][j] = 0
else:
A[k][j] += c * A[i][j]
# Print echelon matrix
print("Echelon Matrix:\t")
pprint(A)
# Solve equation Ax = b for echelon matrix
x = [0 for i in range(n)]
for i in range(n - 1, -1, -1):
# there is no solution
if A[i][i] == 0:
return [0 for i in range(n)]
# normal solution
else:
x[i] = A[i][n]/A[i][i]
for k in range(i-1, -1, -1):
A[k][n] -= A[k][i]*x[i]
return x
# test code
print('Please input the number of variables:')
n = int(input())
# creates a matrix of zeros
A = [[0 for j in range(n+1)] for i in range(n)]
# Read input data
print("Please enter each row separated by a new line:")
for i in range(0, n):
line = map(Fraction, input().split(" "))
for j, el in enumerate(line):
A[i][j] = el
print("Please enter the solution column with values separated by spaces:")
line = input().split(" ")
lastLine = list(map(Fraction, line))
for i in range(0, n):
A[i][n] = lastLine[i]
# Print input
print("\nMatrix:")
pprint(A)
# Calculate solution
x = gauss(A)
# Print solution
print("Result:")
# check results
solution = False
for i in range(n):
if x[i] != 0:
solution = True
# a solution exists
if solution:
for i in range(len(x)):
print("x", i+1, " = ", x[i])
# a solution does not exist
else:
print("No Solution")
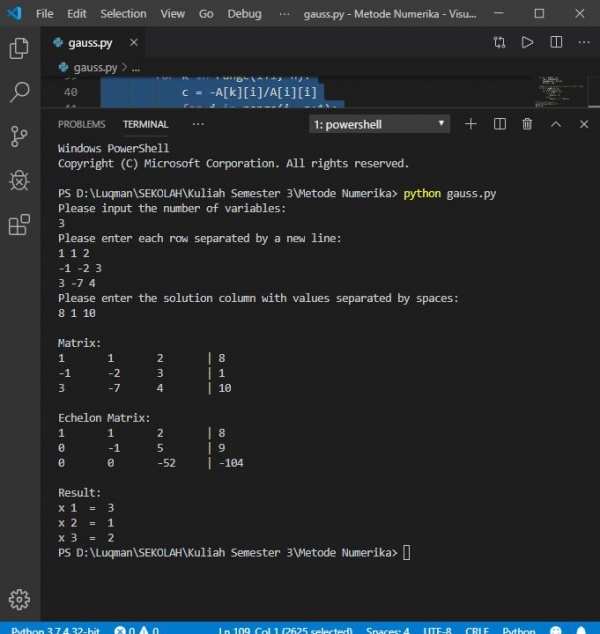
Ketika kode python ini dijalankan, maka akan keluar instruksi untuk mnginput banyak variabel dari sistem persamaan liniar. Setelah menginput variabel, muncul juga instruksi untuk memasukkan isi dari vektor variabel. Berikut ini merupakan sebuah contoh dari penggunaan kode python ini:
Ketika dibandingkan dengan kalkulator eliminasi gauss, didapatkan hasil yang benar-benar sama.
Aplikasi Runge Kutta
2. Algoritma penyelesaian persamaan diferensial dengan Runge Kutta
a. Terdapat sebuah pegas dengan dengan k = 75 N/m, dikaitkan dengan massa sebesar 2.5 kg
b. Massa ditarik dengan fungsi P(t)
c. Jika massa ditarik dalam waktu kurang dari 2 detik, maka gaya yang menarik massa adalah 10t.
d. jika massa ditarik dalam 2 detik atau lebih, maka gaya yang menarik massa adalah 20 N.
e. Regangan terjauh ditentukan oleh besaran gaya yang menarik massa.
f. regangan terjauh dirumuskan dengan metode Runge Kutta, dengan y terjauh = P(t)/m - ky/m