Kelompok 11

Perkenalkan kami dari kelompok 11 beranggotakan:

1. Rivaldo Marta

2. Nyoman Ari Bhaskara

3. Andika Ikshan Kamil

Akan menjelaskan tentang cara penyelesaian Sistem Persamaan Linear untuk matriks 3x3 dengan program python.

Aljabar Linear dalam Python

Intinya dalam pengerjaannya python memiliki suatu library yaitu numpy yang bertujuan untuk memudahkan usernya dalam menyelesaikan suatu persamaan matematik yang kompleks. Didalam numpy ini user dapat menyelesaikan persamaan-persamaan yang rumit dengan contoh Aljabar linear. Kita sebagai user dapat meng-import penghitungan Aljabar Linear dari library numpy dengan command "from numpy import linalg".

Dibawah ini adalah penyelesaian dari soal yang kami ambil dari buku.

Soal Aljabar Linear

Persamaan yang kami miliki adalah:

3X+Y+4Z = 17 2X+3Y+Z = 12 3X+4Y+2Z = 19

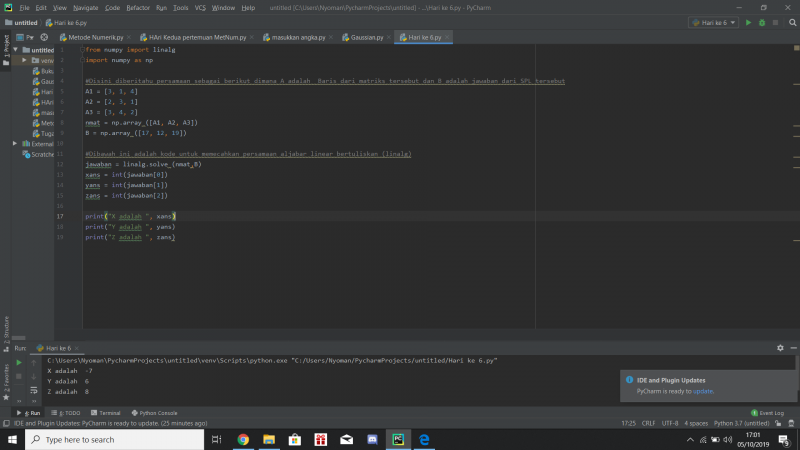
Untuk menghitung penyelesaian dari soal diatas kami menggunakan program seperti dibawah ini:

from numpy import linalg
import numpy as np

#Disini diberitahu persamaan sebagai berikut dimana A adalah  Baris dari matriks tersebut dan B adalah jawaban dari SPL tersebut
A1 = [3, 1, 4]
A2 = [2, 3, 1]
A3 = [3, 4, 2]
nmat = np.array ([A1, A2, A3])
B = np.array ([17, 12, 19])

#Dibawah ini adalah kode untuk memecahkan persamaan aljabar linear bertuliskan (linalg)
jawaban = linalg.solve (nmat,B)
xans = int(jawaban[0])
yans = int(jawaban[1])
zans = int(jawaban[2])

print("X adalah ", xans)
print("Y adalah ", yans)
print("Z adalah ", zans)

Dengan hasil setelah run seperti ini

Yang menghasilkan X(-7),Y(6),dan Z(8)

Tugas Sistem Pegas

Soal yang diberikan merupakan soal sistem pegas yang diberikan gaya eksternal. Dalam Hukum Newton ke dua kita mengetahui bahwa F= m . a. Di soal ini a didapatkan dari y". Maka kita dapatkan rumus Gaya total = gaya yang diberikan pada sistem - gaya pegas. Dijabarkan sebagai berikut m . y" = P(t) - ky. Maka ditemukan fungsi dimana P(t) berlaku 10t N untuk t < 2s dan P(t) berlaku 20 N untuk t >= 2s. Yaitu y" = P(t)/m - ky/m