Kelompok 2

Eliminasi Gauss

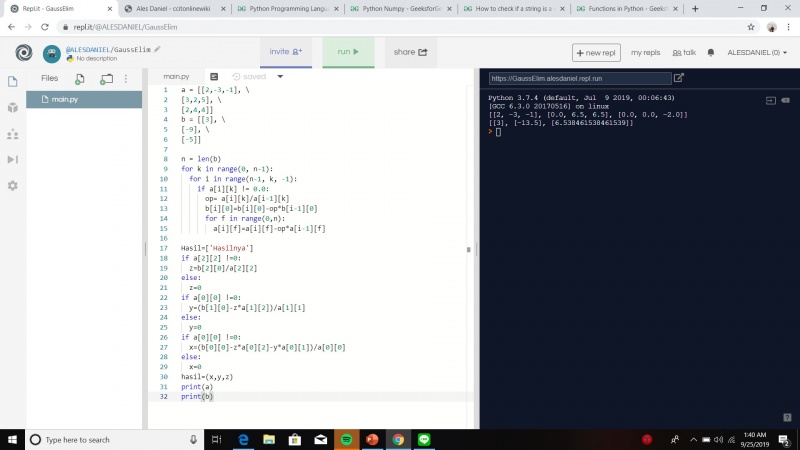
Pengerjaan dilakukan menggunakan algoritma Gauss seperti yang ada di buku Phyton. Namun, yang membedakan adalah tidak menggunakan module pada pengerjaan ini. Berikut adalah algoritma yang sudah dirancang berdasarkan soal pada buku Phyton :

Algoritma yang kami gunakan adalah sebagai berikut:

a = [[2,-3,-1], \
[3,2,5], \
[2,4,4]]
b = [[3], \
[-9], \
[-5]]
n = len(b)
for k in range(0, n-1):
  for i in range(n-1, k, -1):
    if a[i][k] != 0.0:
      op= a[i][k]/a[i-1][k]
      b[i][0]=b[i][0]-op*b[i-1][0]
      for f in range(0,n):
        a[i][f]=a[i][f]-op*a[i-1][f]
Hasil=['Hasilnya']
if a[2][2] !=0:
  z=b[2][0]/a[2][2]
else:
  z=0
if a[0][0] !=0:
  y=(b[1][0]-z*a[1][2])/a[1][1]
else:
  y=0
if a[0][0] !=0:
  x=(b[0][0]-z*a[0][2]-y*a[0][1])/a[0][0]
else:
  x=0
hasil=(x,y,z)
print(a)

Runge-Kutta Method

Pengerjaan dilakukan dan kode dirancang untuk mengikuti contoh soal.

# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01. 
x0 = 0
y = 0
h = 0.01
x = float(input("Masukkan nilai t: "))
if 0 <= x < 2:
  # dydx menyatakan persamaan awal dalam soal.
  # Didapat hasil 4x - 30y karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
  # P(t) dinyatakan dalam x. 
  def dydx(x, y): 
    return (4*x - 30*y) 
  # Ini merupakan implementasi perhitungan Runge-Kutta.
  def rungeKutta(x0, y0, x, h): 
    n = (int)((x - x0)/h)  
    y = y0 
    for i in range(1, n + 1): 
       k1 = h * dydx(x0, y) 
       k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) 
       k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) 
       k4 = h * dydx(x0 + h, y + k3) 
 
       # untuk y selanjutnya 
       y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) 
 
       # untuk x selanjutnya
       x0 = x0 + h 
    return y 
  print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2:
  # Ketika x >= 2, maka variabel x sudah tidak lagi memengaruhi persamaan.
  def dydx(x, y): 
    return (8 - 30*y) 
  def rungeKutta(x0, y0, x, h): 
    n = (int)((x - x0)/h)  
    y = y0 
    for i in range(1, n + 1): 
       k1 = h * dydx(x0, y) 
       k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) 
       k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) 
       k4 = h * dydx(x0 + h, y + k3) 
       y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
       x0 = x0 + h 
    return y 
  print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else:
  print("Mohon masukkan nilai t positif.")