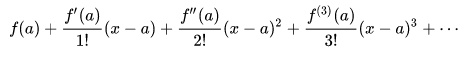Nur Akhmad Fajar

Profil

Nama : Nur Akhmad Fajar

NPM : 1606824774

Jurusan : Teknik Mesin

Deret Taylor (Selasa, 3 September 2019)

Metode Numerik

1. Summary

Pada hari Selasa, 3 September 2019 kami pertama kali diajarkan cara untuk memecahkan masalah dari perhitungan matematika yang sulit. Cara tersebut dinamakan Metode Numerik. Pada hari tersebut kami diajarkan oleh Dr. Ir. Engkos Achmad Kosasih M.T. dan Dr. Ir. Ahmad Indra Siswantara. Metode numerik merupakan salah satu cara untuk mengaproksimasi sebuah fungsi yang terkadang sulit untuk dicari nilai dari akar-akarnya dengan perhitungan sederhana. Pada kelas Metode Numerik hari Selasa, 3 September 2019 kami diperkenalkan dengan Deret Taylor atau Deret Maclaurin. Kami diminta menggunakan program Microsoft Excel untuk mencari nilai sinus dari f(pi/7). Hal ini dapat dipecahkan dengan menggunakan rumus Deret Taylor seperti di bawah ini

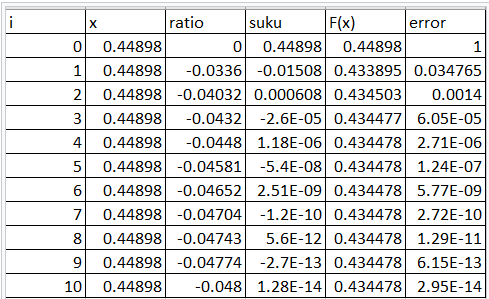
2. Lalu untuk pengaplikasiannya dalam excel berikut saya lampirkan

Tingkatan Bahasa Komputer, merangkai pseudocode (Selasa, 10 September 2019)

Untuk bahasa komputer yang paling rendah dinamakan binary atau bahasa permesinan. Binary tersebut menggunakan angka 1 dan 0 untuk pengoperasiannya. Angkan 1 dan 0 tersebut akan dikombinasikan sehingga dapat membuat suatu perintah. Perintah yang harus diaplikasikan sangatlah banyak, namun kita hanya dapat menggunakan kombinasi antara 1 dan 0 untuk memberi perintah tersebut. Hal ini membuat bahasa tersebut sangat sulit dipahami untuk para pemula. Maka dari itu, dibuatlah bahasa penerjemah yang mana bahasa tersebut akan diterjemahkan kembali ke bahasa binary dengan menggunakan komputer. Penerjemah ini disebut sebagai compiler.

Compiler ini menggunakan aplikasi-aplikasi khusus pada komputer. Berbeda dengan aplikasi yang ada pada komputer, pseudocode adalah bahasa ada pemrograman yang tidak dapat diterjemahkan ke bahasa mesin (binary) karena tidak ada aplikasi yang dapat menerjemahkannya. Berikut adalah contoh pseudocode yang telah dibuat di kelas :

I = r ; err = 1

suku = x

sin = suku

while err > 1e-7

{

ratio = -x^2/((2*I)*(2*I+1))

suku = suku*ratio

err = abs(suku/sin)

sin = sin + suku

I = I+1

}