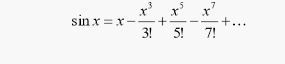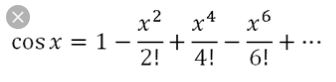Gede Titanandana Andrayuga Pratama

---

Profil

Nama : Gede Titanandana Andrayuga Pratama NPM : 1706036495

Pertemuan 1 (3 September 2019)

Metode Numerik adalah operasi memformulasikan persamaan matematika. Karena batasan kemampuan penghitungan manusia dan kalkulator sederhana maka penghitungan numerik menggunakan komputasi. Salah satu komputasi paling sederhana menggunakan Microsoft Excel. Dengan komputasi dapat melakukan penghitungan dengan efisien dan akurat. Pada materi kelas ini formulasi yang digunakan yaitu menghitung deret taylor dari sin (phi/7). Deret Taylor ini untuk mengakpromisasikan nilai fungsi dengan jumlah dari turunan yang tak berhingga, dalam kasus ini dicari nilai sin (phi/7). Dalam menghitung fungsi ini terdapat beberapa konstanta yaitu :

i = turunan ke-i

x = phi/7

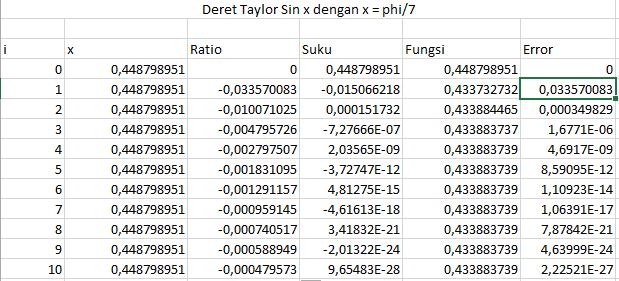
Ratio = suku n / suku n-1 yang dimasukan dengan rumus =-1*(Nilai X)^2/((2*Nilai i)*(2*Nilai i + 1))

Suku = Dimasukan dengan rumus = Suku ke n*Rasio pada nilai i

Fungsi = Dimasukan dengan rumus =Fungsi ke n-1 + Suku ke n

Error = Dimasukan dengan rumus =ABS(suku ke n/fumgsi ke n-1

Rumus Taylor Series

Rumus Taylor Series Sin (x)

Berdasarkan hasil komutasi di tabel maka nilai sin(phi/7) = 0,43388

Tugas 1

1) Akpromisasikan nilai cos(phi/7)

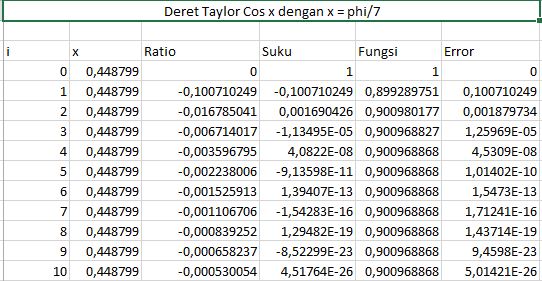
Melihat dari deret taylor cox (x) maka rationya =-1*(Nilai X)^2/((2*Nilai i)*(2*Nilai i - 1))

Berdasarkan tabel maka nilai cos (phi/7) = 0,90097

2) Akpromisasikan e^(phi/7)