Calvin rahmat pratama

Biodata Diri

Nama: Calvin Rahmat Pratama

NPM: 1806200974

Tempat,tanggal lahir: Batam,14 Oktober 2000

Hobi: Gaming dan Golf

Saya adalah mahasiswa FTUI angkatan 2018 dari jurusan Teknik mesin dan saya adalah salah satu ciptaan terbaik dari Tuhan yang Maha Esa karena pada prinsipnya Tuhan yang Maha Esa itu mendesain manusia dengan sebaik baiknya makhluk.

Teknik Mesin merupakan program studi yang saya gemari dikarenakan ayah saya juga merupakan lulusan Teknik Mesin.

Tujuan Pembelajaran

1. Memahami konsep dengan dengan baik tentang dasar-dasar metode numerik.

2. Mampu menerapkan pemahaman konsep tersebut didalam permodelan numerik.

3. Mampu menerapkan metode numerik dipersoalan keteknikan.

4. Sebagai nilai tambah bagi saya agar menjadi manusia yang beradab seperti pada Sila ke-2 Pancasila.

Metode Numerika

Sejauh ini yang dapat saya ketahui dalam metode numerika adalah metode numerika dapat menyelesaikan permasalahan yang tidak dapat diselesaikan oleh metoda analisis saya juga mempelajari cara menggunakan excel untuk menyelesaikan beberapa permasalahan metode numerika. Seperti menggunakan psuedocode dan metode newton rhapson.

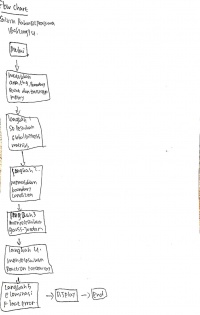
Review Minggu 1

Untuk pertemuan pertama saya mempelajari cara menggunakan OpenModelica dimulai dari persamaan yang cukup sederhana, OpenModelica sendiri merupakan aplikasi penghitungan permodelan yang lumayan kompleks, sehingga OpenModelica itu sendiri sangat membantu saat menyelesaikan permodelan masalah mulai dari yang cukup mudah sampai ke cukup kompleks

Review Minggu 2

Alasan mengapa menggunakan openmodelica dibanding aplikasi lainnya

- Secara penggunanaan lebih digunakan untuk permodelan bukan untuk programming

- Didalam melakukan perhitungan kode yang diinput di modelica itu di terjemahkan ke Bahasa C dan kemudian diterjemahkan lagi ke Bahasa permesinan sehingga bisa melakukan perhitungan permodelan

- Paling penting adalah openmodelica itu gratis

Pada pertemuan kedua saya juga mempelajari menggunakan modelica untuk "memanggil" fungsi. Pada pertemuan kedua juga mempelajari mengenai Fungsi tambah yang mana terlebih dahulu dari permodelan masalah di translasi kan terlebih dahulu ke dalam bahasa C++ yang nantinya akan di proses menjadi data-data perhitungan.

Review Minggu 3

Pada minggu ke tiga ini saya mencoba untuk mempelajari kembali untuk membuat fungsi modelica 9x12 dengan metode gauss atau menggunakan metode lain, kemudian mencoba mengimplementasikan psuedocode pada Figure 9.4 di modelica yang mana nantinya akan di test coding dengan example 9.5.

Tugas Minggu 3

model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary coundition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];

//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Matrices(X1);
G1:=k1*GlobalMatrices(K1,N,p1a,p1b);

K2:=Matrices(X2);
G2:=k2*GlobalMatrices(K2,N,p2a,p2b);

K3:=Matrices(X3);
G3:=k3*GlobalMatrices(K3,N,p3a,p3b);

K4:=Matrices(X4);
G4:=k4*GlobalMatrices(K4,N,p4a,p4b);

K5:=Matrices(X5);
G5:=k5*GlobalMatrices(K5,N,p5a,p5b);

K6:=Matrices(X6);
G6:=k6*GlobalMatrices(K6,N,p6a,p6b);

G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Matrices(N,Ginitial,SolMat,XMat);

end Trusses;

Fungsi Panggilan

Matriks
function Matrices
input Real A;
protected
Real Y;
public
output Real X[4,4];
protected
Real float_error = 10e-10;
protected
final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
   
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*
Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
(Modelica.Math.sin(Y))^2,
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)
*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,
Modelica.Math.cos(Y)*Modelica.Math.sin(Y); 

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
-(Modelica.Math.sin(Y))^2,
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then X[i,j] := 0;
end if;
end for;
end for;

end Matrices;

Global Matriks

function GlobalMatrices

input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];

end GlobalMatrices;

Reaction Matrices

function Reaction_Matrices
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
protected
Real X[N,1];
public
output Real Sol[N];
protected
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
if abs(X[i,1]) <= float_error then
  X[i,1] := 0;
end if;
end for;

for i in 1:N loop
Sol[i]:=X[i,1];
end for;

end Reaction_Matrices;

Gauss Jordan

input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;

algorithm
X:=Modelica.Math.Matrices.solve(A,B);

for i in 1:N loop
 if abs(X[i]) <= float_error then
   X[i] := 0;
 end if;
end for;

end Gauss_Jordan;

|}

Kuis 1 Metode Numerik

Tugas 4

class truss_3d_try
//define initial variable
parameter Integer Points=4; //Number of Points
parameter Integer Trusses=3; //Number of Trusses
parameter Real Area=0.0015; //Area
parameter Real Elas=70e9; //Elasticity

//define connection
parameter Integer C[Trusses,2]=[1,2;
                                1,3;
                                1,4];
                             
//define coordinates (please put orderly)
parameter Real P[Points,3]=[2,0,0;
                            0,0,1.5;
                            0,0,-1.5;
                            0,1.5,0]; 

//define external force (please put orderly)
parameter Real F[Points*3]={0,-5000,0,
                            0,0,0, 
                            0,0,0, 
                            0,0,0}; 

//define boundary
parameter Integer b[:]={2,3,4};

//solution
Real displacement[N], reaction[N];

protected
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, X[3,3];

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
end for;
      //Solving Matrix
      L:=Modelica.Math.Vectors.length(q2-q1);
      cx:=(q2[1]-q1[1])/L;
      cy:=(q2[2]-q1[2])/L;
      cz:=(q2[3]-q1[3])/L; 
      X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                        cy*cx,cy^2,cy*cz;
                        cz*cx,cz*cy,cz^2];

      //Transforming to global matrix
      g:=zeros(N,N); 
      for m,n in 1:3 loop
        g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
        g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
        g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
        g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
      end for;  

G_star:=G+g;
G:=G_star;
end for;

//Implementing boundary
for i in boundary loop
for j in 1:N loop
  G[i,j]:=id[i,j];
end for;
end for;

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction
reaction:=(G_star*displacement)-F;

//Eliminating float error
for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
end truss_3d_try;

Pertemuan 16/12/2020

Aplikasi Metode Numerik Dalam Kasus Optimasi

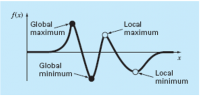
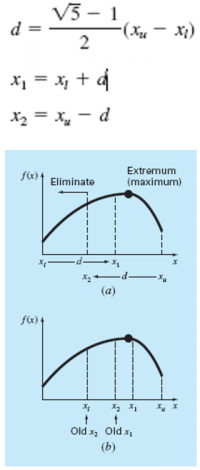
Bracket Optimization Using the Golden Ratio Ada Satu Grafik Fungsi Yang Memiliki Nilai F(X) Global Maksimum Dan Lokal Maksimum Serta F(X) Global Minimum Dan Lokal Minimum

Menentukan Global Maksimum dengan cara melakukan optimasi dengan nilai X untuk mendapatkan F(X) Maksimum

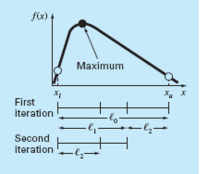
1. Menentukan batasan titik awal terendah (xL) dan tertinggi (xH)

2. Mendapatkan nilai x1 dan x2 dari golden ratio (d)

3. Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru

4. Mendapatkan nilai x1 dan x2 baru

f(x1)>f(x2)

domain x disebelah kiri x2 dapat dieliminasi

xL=x2 untuk iterasi berikutnya

xu=xu lama

f(x2)>f(x1)

Domain x disebelah kanan x1 dapat dieliminasi

xu=x1 untuk iterasi berikutnya

xL=xL lama

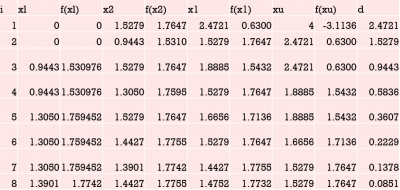
Perhitungan Excel

Tugas Besar Metode Numerik

Tema:

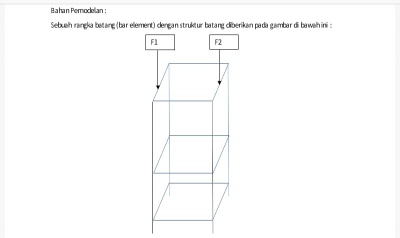
-Aplikasi Metoda Numerik dalam Optimasi Desain Struktur Rangka Sederhana

Sinopsis:

Plotting:

-Beban hanya akan terdistribusi pada node

-Memiliki nilai Safety Factor minimal 2

-Memiliki Batas Displacement sekitar 0.0001 m (truss paling atas)

-Ketinggian pada masing masing sama yaitu 0.6m

Data

Program

Program penghitungan pada Displacement,Reaction Force,Stress dan Safety Factor

model Tugas_Besar_Calvin

//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=170e6; //Yield Strength (Pa)
parameter Real Area=0.09632;   //Area L Profile (Dimension=0.04, Thickness=0,003) (m2)
parameter Real Elas=193e9;     //Elasticity SS 316L  (Pa)

//define connection
parameter Integer C[:,2]=[1,5; 
                          2,6;
                          3,7;
                          4,8;
                          5,6;  //1st floor
                          6,7;  //1st floor
                          7,8;  //1st floor
                          5,8;  //1st floor
                          5,9;
                         6,10;
                         7,11;
                         8,12;
                         9,10; //2nd floor
                         10,11;//2nd floor 
                         11,12;//2nd floor
                          9,12; //2nd floor
                          9,13;
                         10,14;
                         11,15;
                         12,16;
                         13,14;//3rd floor
                         14,15;//3rd floor
                         15,16;//3rd floor
                         13,16];//3rd floor
                                                             
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1;     //1
                       -0.3,-0.375,0,1,1,1;    //2
                       -0.3,0.375,0,1,1,1;     //3
                       0.3,0.375,0,1,1,1;      //4
                          
                       0.3,-0.375,0.6,0,0,0;   //5
                       -0.3,-0.375,0.6,0,0,0;  //6
                       -0.3,0.375,0.6,0,0,0;   //7
                       0.3,0.375,0.6,0,0,0;    //8
                           
                       0.3,-0.375,1.2,0,0,0;   //9
                       -0.3,-0.375,1.2,0,0,0;  //10  
                       -0.3,0.375,1.2,0,0,0;   //11
                       0.3,0.375,1.2,0,0,0;    //12
                           
                       0.3,-0.375,1.8,0,0,0;   //13
                       -0.3,-0.375,1.8,0,0,0;  //14
                       -0.3,0.375,1.8,0,0,0;   //15
                        0.3,0.375,1.8,0,0,0];   //16
                          
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,-500, 
                            0,0,-1000, 
                            0,0,-1000, 
                            0,0,-500}; 

//solution
Real displacement[N], reaction[N];
Real check[3]; 

Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
 
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4; 

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
 for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
 end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                     cy*cx,cy^2,cy*cz;
                     cz*cx,cz*cy,cz^2]; 

  //Transforming to global matrix
  g:=zeros(N,N); 
  for m,n in 1:3 loop
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
  end for;  

G_star:=G+g;
G:=G_star;
end for;

//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-2,a]:=0;
    G[(x*3)-2,(x*3)-2]:=1;
  end for;
end if;
if P[x,5] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-1,a]:=0;
    G[(x*3)-1,(x*3)-1]:=1;
  end for;
end if;
if P[x,6] <> 0 then
  for a in 1:Points*3 loop
    G[x*3,a]:=0;
    G[x*3,x*3]:=1;
  end for;
end if;
end for;

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction
reaction:=(G_star*displacement)-F;

//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;

//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;

//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
 q1[j]:=P[C[i,1],j];
 q2[j]:=P[C[i,2],j];
 dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
     
  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
               cy*cx,cy^2,cy*cz;
               cz*cx,cz*cy,cz^2];
  
  Str:=(X*dis);
  stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;

//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
  safety[i]:=Yield/stress1[i];
else
  safety[i]:=0;
end if; 
end for;

end Tugas_Besar_Calvin;

Curve Fitting

function Kurva

input Real X[:];
input Real Y[size(X,1)];
input Integer order=2;
output Real Coe[order+1];

protected
Real Z[size(X,1),order+1];
Real ZTr[order+1,size(X,1)];
Real A[order+1,order+1];
Real B[order+1];

algorithm

for i in 1:size(X,1) loop
for j in 1:(order+1) loop
Z[i,j]:=X[i]^(order+1-j);
end for;
end for;
ZTr:=transpose(Z);

A:=ZTr*Z;
B:=ZTr*Y;
Coe:=Modelica.Math.Matrices.solve(A,B);

end Kurva;

Gold Optimization

model Gold_Opt

parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=64e-6;
parameter Real xhi=215e-6; 
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error

Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt,  fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2; 

algorithm
xl := xlo; 
xu := xhi;
y  := Kurva(xd,yd);
 
for i in 1:N loop
 d:= R*(xu-xl);
 x1[i]:=xl+d;
 x2[i]:=xu-d;
 f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
 f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
 xint:=xu-xl;

if f1[i]>f2[i] then
  xl:=x2[i];
  xopt:=x1[i];
  fx:=f1[i];
  else
    xu:=x1[i];
    xopt:=x2[i];
    fx:=f2[i];
end if;

ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
  break;
end if;
end for;

end Gold_Opt;

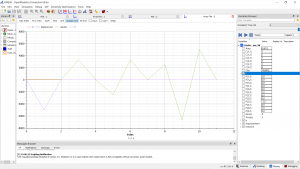
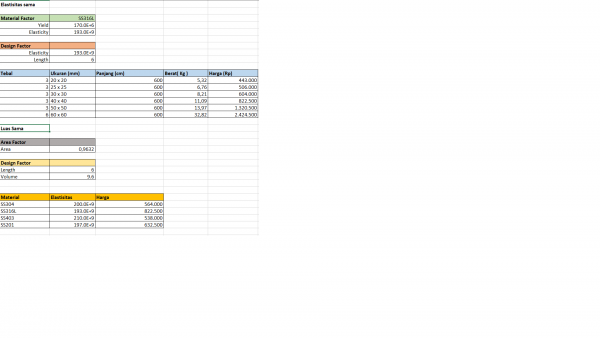
Hasil

Kesimpulan Dengan penggunaan luas area sebsar 171 mm^2 atau material siku 40x40 dengan thickness 3mm, maka material yang paling optimal untuk digunakan adalah material dengan tingkat elastisitas sebesar 193 GPa

Material yang terletak dalam range elastisitas ini adalah material SS316L dengan tingkat elasitisas sama dengan nilai optimal yaitu 193 GPa.

UAS

Kinematika

Kinematika merupakan bagian dari mekanika yang mempelajari tentang gerak pada suatu benda tanpa mempertimbangkan penyebab benda itu bergerak. Benda dikatakan bergerak apabila mengalami perubahan posisi dari titik acuannya.

Rumus Terkait

Gerak Lurus

1.Perpindahan (As)

Yaitu perubahan posisi awal so ke posisi akhir s, berlaku:

Delta s = S-So

2. Kecepatan dan Kelajuan Rata-Rata

Dua jenis kecepatan yaitu:

Kecepatan Rata-rata (v) perpindahan

V= perpindahan/waktu=Delta s/Delta t= S-So/t-to

Kelajuan Rata-rata (v)

V= jarak/Waktu= s/t 

Kecepatan Sesaat(V)

V= ds/dt

3. Percepatan

Yaitu perubahan kecepatan benda dalam selang waktu tertentu.

Percepatan Rata-rata

a=Delta v/Delta t= v-vo/t-to

Percepatan Sesaat

a=dv/dt

4.Gerak Lurus Beraturan (GLB)

Yaitu Gerak benda pada lintasan lurus dengan kecepatan konstan dengan

percepatan = 0.

Fluida Statis

Hasil diskusi dengan ChatGPT

Apa itu Fluida Statis

Fluida statis adalah fluida yang diam, artinya tidak bergerak atau mengalir. Istilah "statis" mengacu pada fakta bahwa fluida berada dalam keadaan setimbang, yang berarti bahwa gaya yang bekerja pada titik tertentu dalam fluida seimbang.

Dalam fluida statis, tekanan pada titik tertentu di dalam fluida adalah sama ke segala arah. Ini dikenal sebagai hukum Pascal, yang menyatakan bahwa tekanan yang diterapkan pada fluida dalam wadah tertutup diteruskan secara merata ke segala arah.

Perilaku fluida statis diatur oleh prinsip hidrostatika, yang merupakan cabang mekanika fluida yang berhubungan dengan fluida diam. Hidrostatik melibatkan studi tentang tekanan, kepadatan, dan gravitasi yang berhubungan dengan cairan saat istirahat.

Beberapa konsep kunci dalam hidrostatik meliputi:

Tekanan: Gaya per satuan luas yang diberikan oleh fluida pada permukaan. Satuan SI untuk tekanan adalah Pascal (Pa), yang sama dengan satu Newton per meter persegi. Daya apung : Gaya ke atas yang dikerjakan oleh fluida pada benda yang terbenam di dalamnya. Gaya ini sama dengan berat fluida yang dipindahkan oleh benda. Prinsip Archimedes: Gaya apung pada benda yang dicelupkan ke dalam fluida sama dengan berat fluida yang dipindahkan oleh benda tersebut. Tekanan hidrostatik: Tekanan yang diberikan oleh fluida pada kedalaman tertentu, yang meningkat dengan bertambahnya kedalaman karena berat fluida di atasnya. Aplikasi hidrostatik termasuk desain bendungan, lift hidrolik, dan kapal selam, serta studi tentang tekanan atmosfer dan perilaku cairan dalam tubuh manusia.

Apa yang dimaksud dengan Manometer

Manometer adalah alat yang digunakan untuk mengukur tekanan, biasanya dalam cairan. Ini terdiri dari tabung berbentuk U yang diisi dengan cairan, biasanya merkuri atau air, dan sumber tekanan diterapkan ke salah satu ujung tabung, sedangkan ujung lainnya terbuka ke atmosfer atau tekanan referensi.

Ketika tekanan diterapkan pada salah satu ujung tabung, cairan di lengan tabung itu naik, menciptakan perbedaan ketinggian cairan antara kedua lengan tabung. Perbedaan tingkat cairan sesuai dengan perbedaan tekanan antara dua titik yang diukur.

Perbedaan ketinggian antara kedua lengan tabung sebanding dengan perbedaan tekanan, menurut persamaan:

∆P = ρgh

di mana ΔP adalah perbedaan tekanan, ρ adalah densitas fluida dalam manometer, g adalah percepatan gravitasi, dan h adalah perbedaan ketinggian antara dua level fluida.

Manometer umumnya digunakan dalam berbagai aplikasi, termasuk mengukur tekanan dalam pipa, tangki, dan sistem HVAC. Mereka juga digunakan untuk mengukur perbedaan tekanan kecil dalam percobaan dan penelitian ilmiah.

Selain manometer tabung-U, ada jenis manometer lain, termasuk manometer tabung miring dan manometer digital, yang menggunakan sensor elektronik untuk mengukur tekanan.

‘’’Dapatkah kondisi lingkungan mempengaruhi bacaan dalam manometer’’’

Ya, kondisi lingkungan pasti dapat mempengaruhi pembacaan manometer. Manometer adalah instrumen sensitif yang mengukur perbedaan tekanan antara dua titik. Setiap perubahan dalam kondisi lingkungan dapat menyebabkan perbedaan tekanan yang diukur berubah, yang dapat menyebabkan pembacaan yang tidak akurat. Berikut adalah beberapa cara di mana kondisi lingkungan dapat mempengaruhi pembacaan manometer:

1.Temperatur: Perubahan temperatur dapat mempengaruhi volume gas di dalam tabung manometer, yang dapat mengubah ketinggian cairan di dalam tabung sehingga mempengaruhi pembacaan.

2.Tekanan atmosfer: Perubahan tekanan atmosfer juga dapat memengaruhi pembacaan manometer. Perubahan tekanan atmosfer dapat menyebabkan perbedaan tekanan yang diukur berubah, menghasilkan pembacaan yang berbeda.

3.Kelembaban: Perubahan kelembaban dapat menyebabkan penguapan atau penyerapan cairan di dalam tabung manometer, yang dapat mengubah volume gas di dalam tabung dan mempengaruhi pembacaan.

4.Getaran dan guncangan mekanis: Setiap getaran atau guncangan mekanis dapat menyebabkan cairan di dalam tabung manometer bergerak, menyebabkan pembacaan yang tidak akurat.

Untuk mendapatkan pengukuran yang akurat dengan manometer, penting untuk memastikan bahwa kondisi lingkungan dikendalikan dan memperhitungkan potensi sumber kesalahan.

Densitas dan viskositas fluida yang diukur: Jika densitas dan viskositas fluida yang diukur berubah karena suhu, tekanan, atau kelembapan, hal ini dapat memengaruhi keakuratan pembacaan manometer.