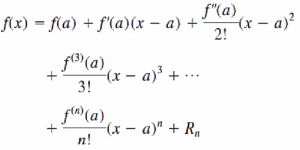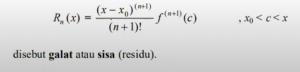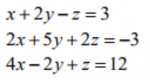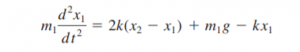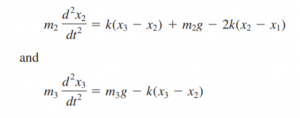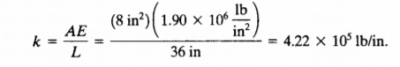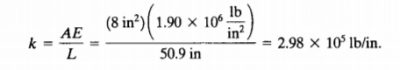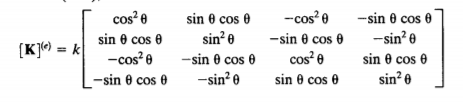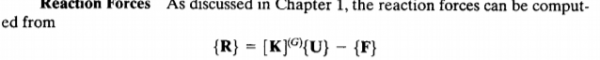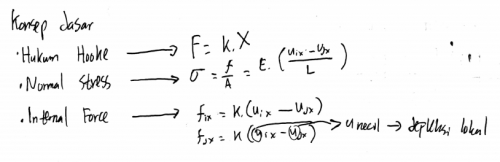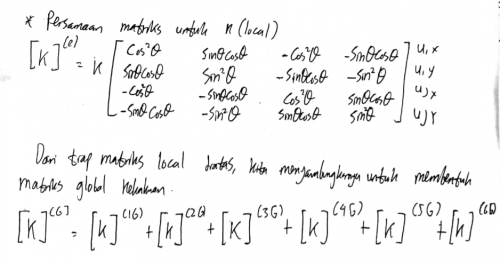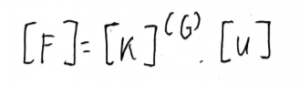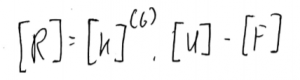Metnum03-Bolonni Nugraha
Contents
- 1 BIODATA DIRI
- 2 Pertemuan 1 (9 November 2020)
- 3 Pertemuan 2 (16 November 2020)
- 4 Pertemuan 3 (23 November 2020)
- 5 Pertemuan 4 (30 November 2020)
- 6 Pertemuan 5 (7 Desember 2020)
- 7 Pertemuan 6 (14 Desember 2020)
- 8 Pertemuan 7 (21 Desember 2020)
- 9 Tugas Besar: Aplikasi Metoda Numerik dalam Optimasi Statika Struktur Rangka Sederhana space truss (3D)
- 10 Pertemuan 8 (4 Januari 2020)
- 11 UAS
BIODATA DIRI
Nama : Bolonni Nugraha
Tempat/Tanggal lahir: Bekasi, 21 Desember 1999
NPM : 1806181741
Fakultas/ Jurusan : Teknik/ Teknik Mesin
Kelas: Metoda Numerik 03
Pertemuan 1 (9 November 2020)
Pada pertemuan kali kembali dilaksanakan secara PJJ. Pak Dai kembali mengingatkan pentingnya perhitungan secara numerik untuk membantu kita memecahkan masalah.
Berikut merupakan dasar penilaian dan objektif dari Pak Dai yang merupakan apa yang diharapkan dari setiap individu mahasiswa pada akhir semester nantinya
1. Memahami konsep, dari konsep melahirkan prinsip/pembentukan rumusan
2. Untuk menunjukan kepahaman, menerapkan konsep untuk memecahkan masalah
3. Perumusan keteknikan
4. Mendapatkan nilai tambah di dalam usaha mengenal diri sendiri
Untuk minggu pertama, Pak Dai memberikan tugas untuk menulis apa yang telah kami pelajari selama setelah semester yang lalu pada mata kuliah Metode Numerik.
Mengapa kita membutuhkan perhitungan secara numerik? Menurut Pak Engkos, selaku dosen Metode Numerik sebelum UTS, dikarenakan banyaknya perhitungan yang tidak bisa dilakukan secara eksak, khususnya perhitungan di bidang Engineering. Pendekatan Numerik menggunakan perhitungan berulang untuk mendekati nilai eksak. Berikut adalah garis besar ilmu yang saya dapatkan sebelum UTS.
1. Mencari error pada Pembulatan dan Deret Taylor
Dalam kasus khusus di mana a = 0, deret ini disebut juga sebagai Deret Maclaurin.
Deret ini merubah suatu F(x) menjadi polinomial
Errornya sendiri bukan terhadap true value, karena beberapa fungsi pada suatu titik tidak menemukan suatu nilai yang pasti, melainkan eror perbandingan value baru dengan value lama yang diabsolutkan.
2. Penyelesaian sistem persamaan
Melakukan pencarian akar-akar persamaan secara numerik. Secara garis besar dilakukan secara Brackething Method (Closed Method, menggunakan batas bawah dan batas atas), seperti pada Graphical Methods, Bisection Methods dan False-Position Methods, dan Open Method (menggunakan 1 titik), seperti pada Fixed-Point Iteration, Newton-Rapshon, dan Secant Method.
3. Regresi Linier
Regresi adalah pemodelan asosiasi antara satu variabel dependen dengan satu/lebih variabel independen. Pada kasus kali ini yang dibahas adalah pola sebaran data yang cenderung linier. Kegunaannya adalah memprediksi sebaran data selanjutnya berdasarkan data-data yang telah dimiliki sebelumnya
4. Numerical Differentiation
Pertemuan 2 (16 November 2020)
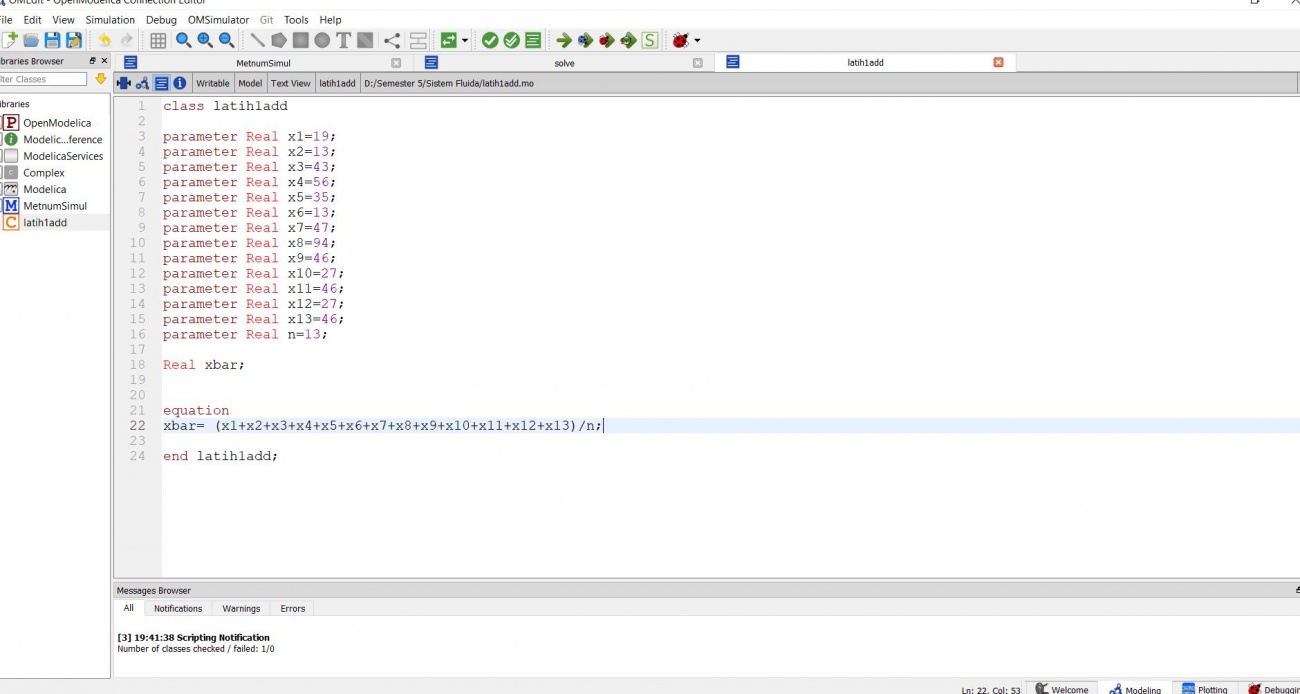
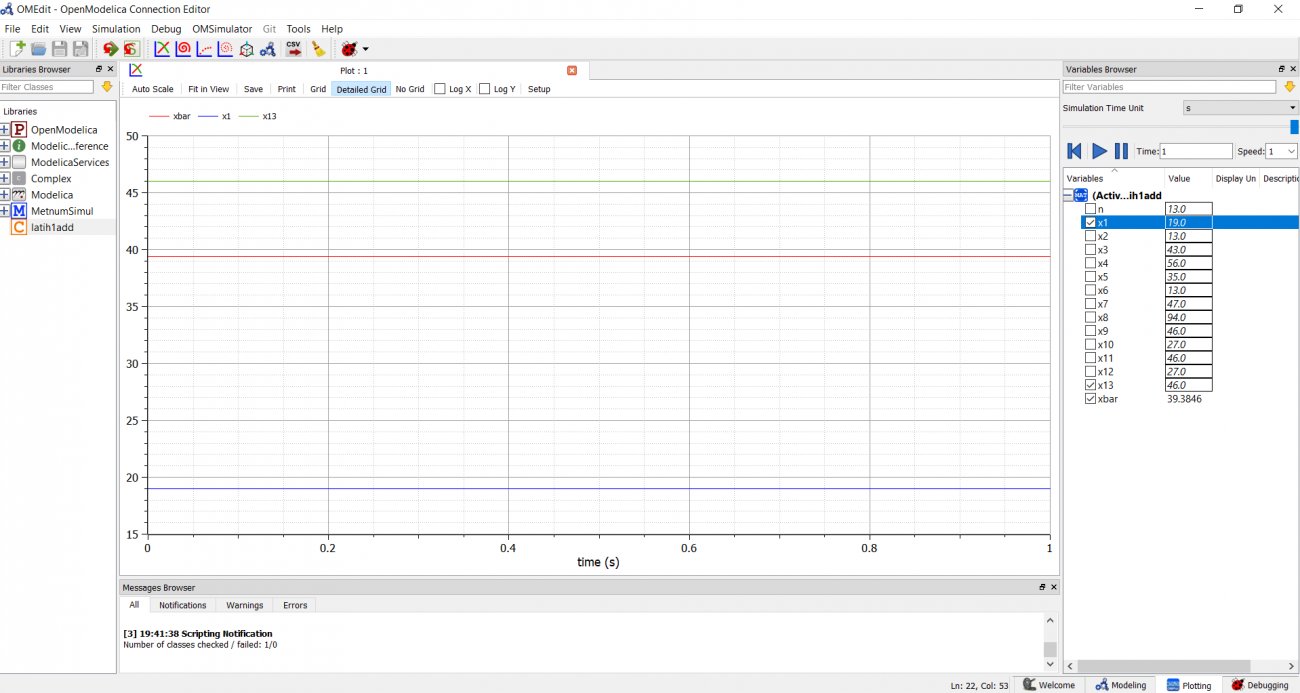
Pada pertemuan kali ini, sambil mahasiswa diminta untuk memberikan progress pembelajaran menggunakan modelica, Pak Dai meminta mahasiswa untuk mensimulasikan coding sederhana mencari nilai rata-rata dari beberapa sample. Berikut lampiran percobaan simulasi saya
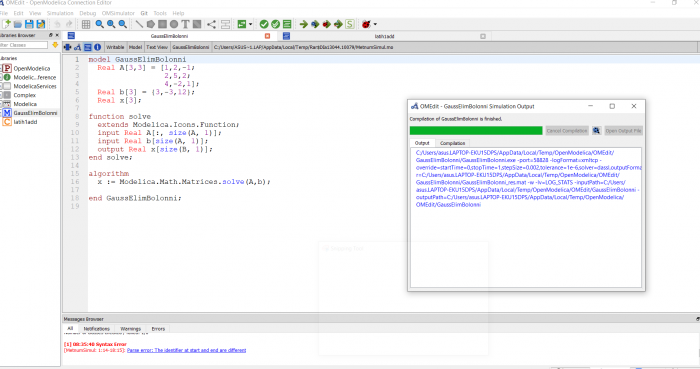
Yang berikutnya, Pak Dai juga meminta mahasiswa untuk membuat coding penyelesaian persamaan aljabar linier dengan metode yang sudah dipelajar. Disini saya menggunakan metode Gauss Elimination
Sehingga diperoleh
x=3
y=-1
z=-2
Pertemuan 3 (23 November 2020)
Pada pertemuan kali ini, Pak Dai menggambarkan hubungan pembelajaran kita pada kelas metode numerik dengan aplikasinya pada penyelesaian permasalahan teknik. Berikut adalah tahapan-tahapannya:
- masalah teknik
- analisis masalah
- model matematis
- model numerik
- komputer
- solusi
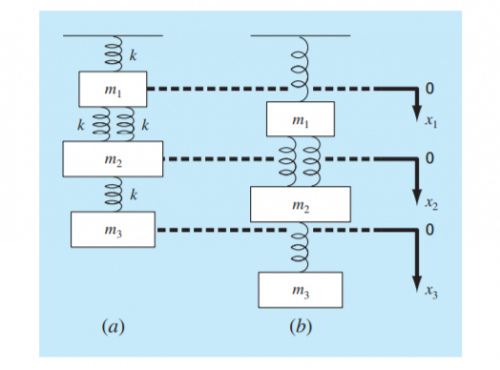
Untuk kita lebih memahami tahapan-tahapan ini, diberikan contoh kasus pada spring mass sebagai berikut:
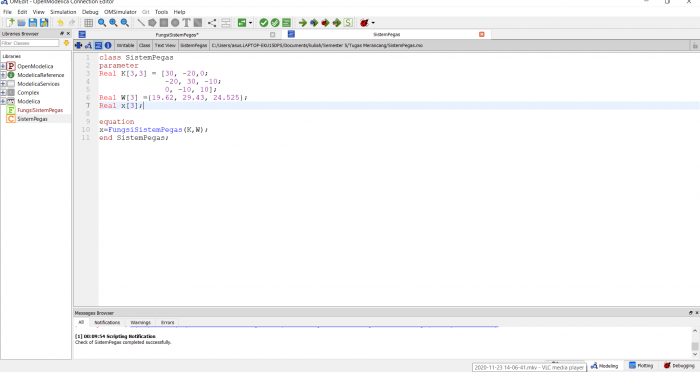
Dari persamaan diatas kita ubah jadi bentuk matriks dan diselesaikan dengan eliminasi gauss
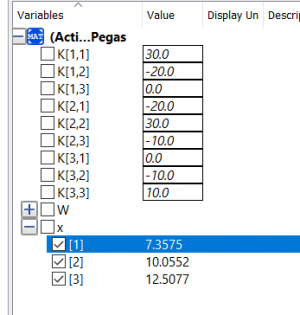
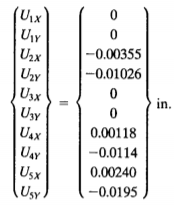
Didapatkanlah nilai variabel dari x sebagai berikut
Tugas Trusses
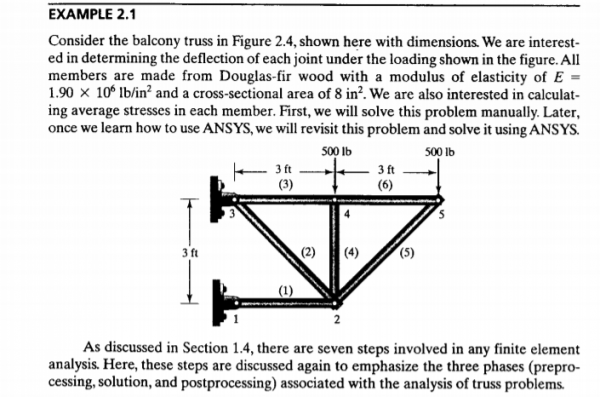
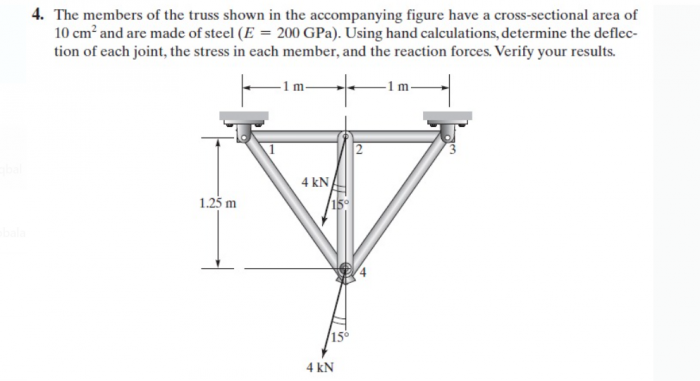
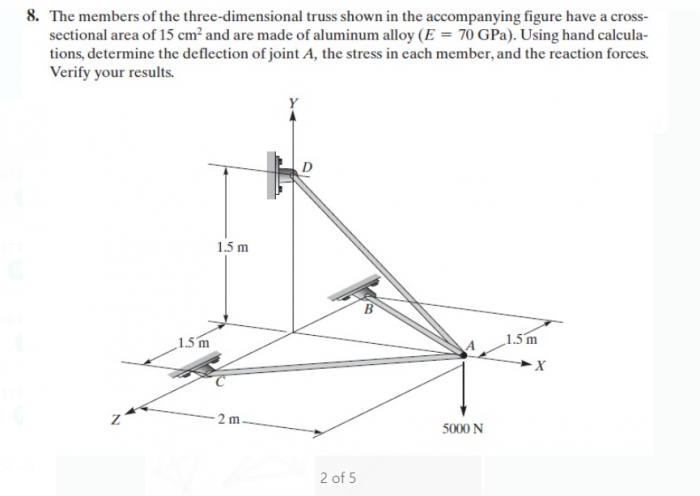
Di akhir kelas, Pak Dai memberikan contoh kasus lain sebagai tugas selanjutnya. Contoh kasus permasalahan tekniknya adalah soal statik struktur. Kami diminta untuk mencari nilai displacement dan gaya reaksinya.
Tahapan penyelesaian:
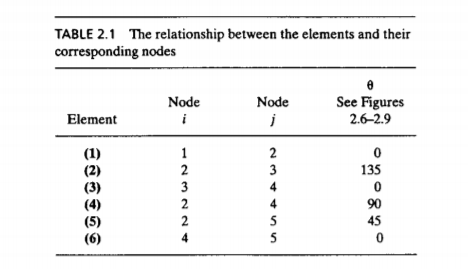
1. Untuk memudahkan, pertama-tama kita konsiderasikan batang menjadi elemen dan titik temu sebagai node(simpul)
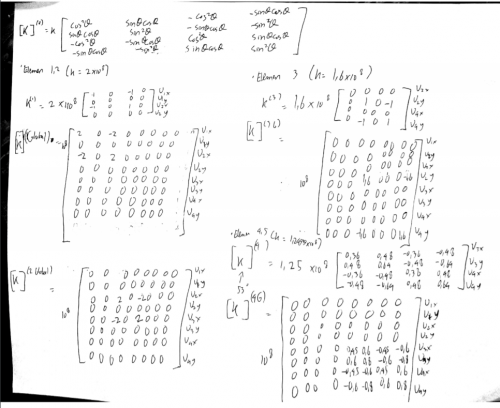
2. Mencari nilai konstanta kekakuan elemen. Karena pada elemen (1),(3),(4),dan(6) memiliki panjang, luas penampang, dan modulus elastisitas yang sama, sehingga memiliki nilai yang sama sebagai berikut:
Sementara pada (2) dan (5) sebagai berikut:
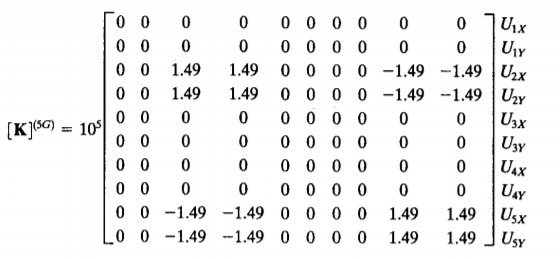
3. Membuat matriks kekakuan tiap elemen
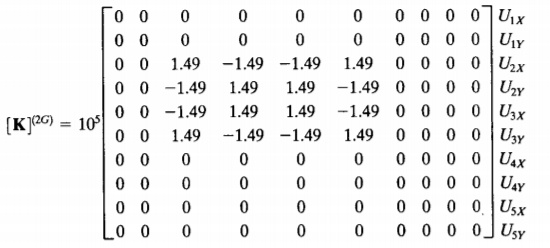
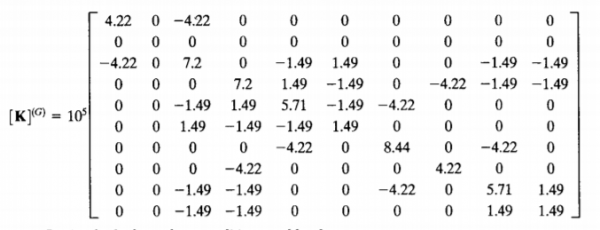
4. Menyambungkan elemen-elemen dan membentuk matriks global kekakuan
Kita sederhanakan:
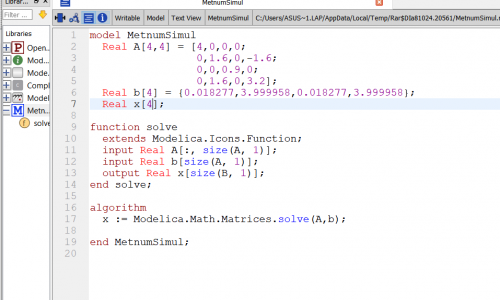
5. Menerapkan kondisi batas dan beban
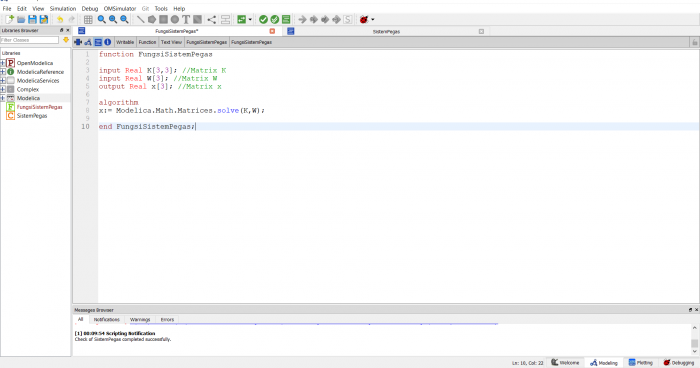
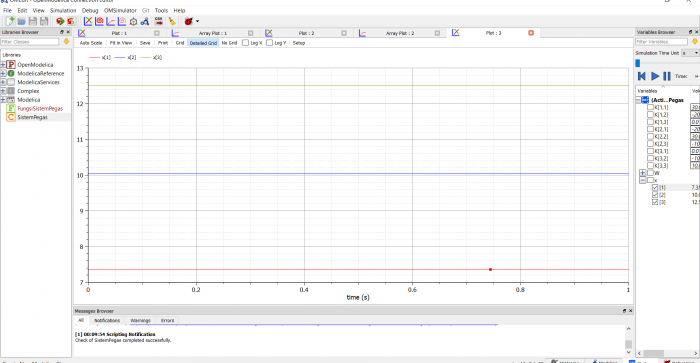
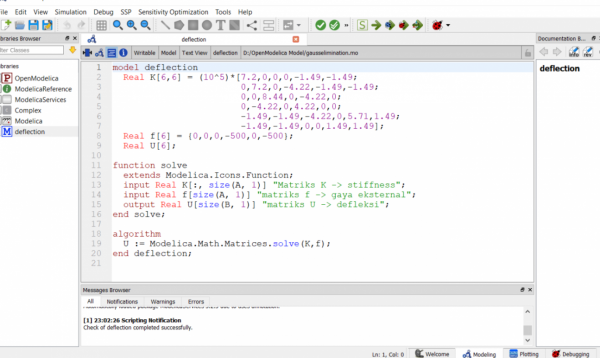
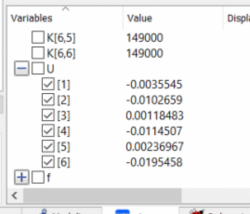
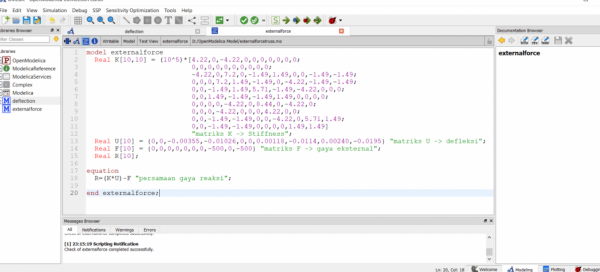
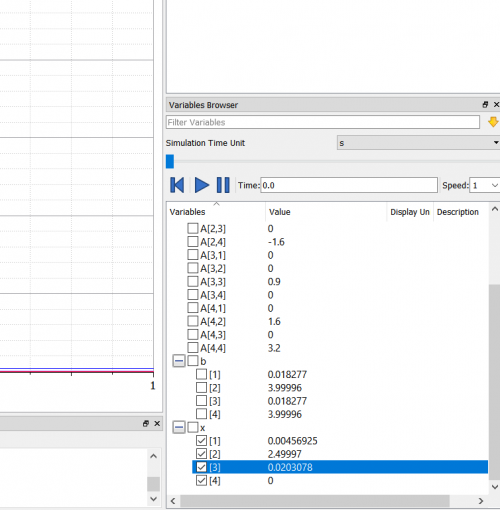
6. Mencari solusi persamaan (displacement) dengan bantuan software OpenModelica
Sudah sesuai dengan buku
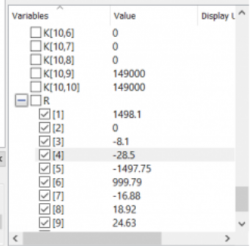
7. Mencari nilai gaya reaksi
8. Mencari internal force dan normal stress
Pertemuan 4 (30 November 2020)
Quiz
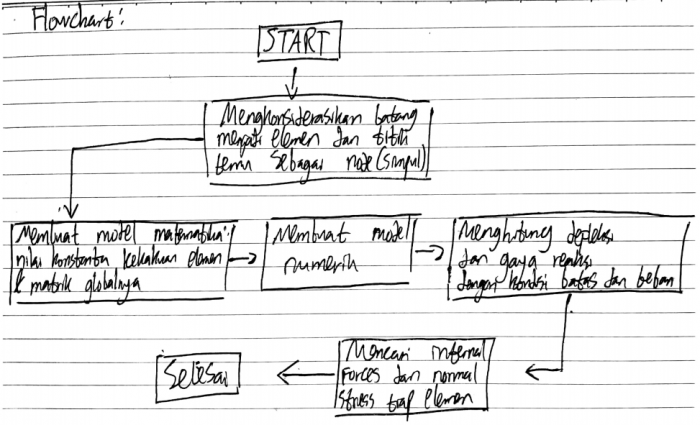
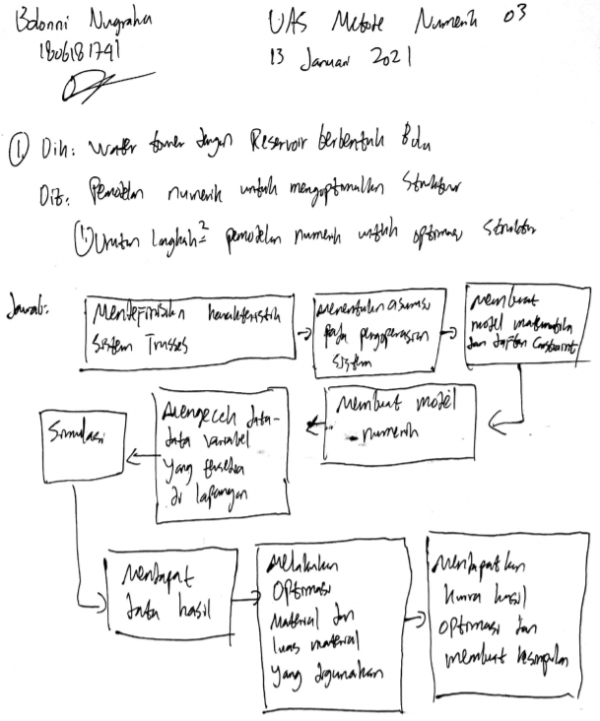
Buatlah flowchart penyelesaian masalah teknik berikut!
Flowchart kedua soal kurang lebih sama sebagai berikut:
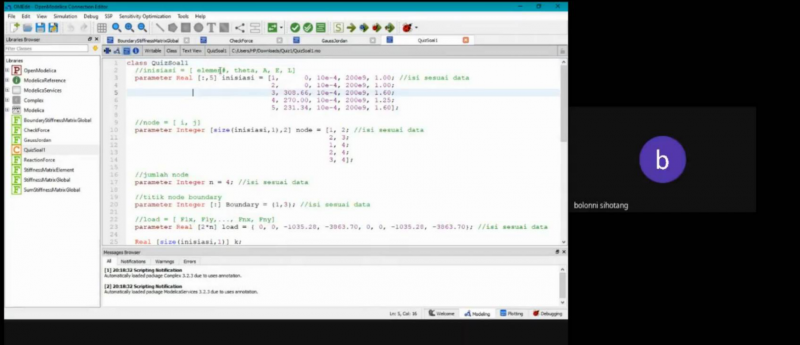
Beberapa dokumentasi perhitungan:
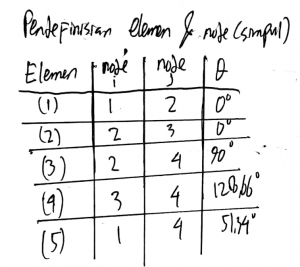
No.4
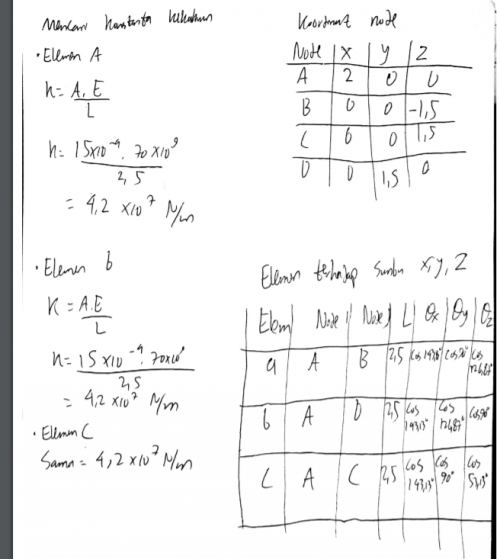
Pendefinisian elemen & node (simpul)
Pencarian konstanta kekakuan
Konsep dasar
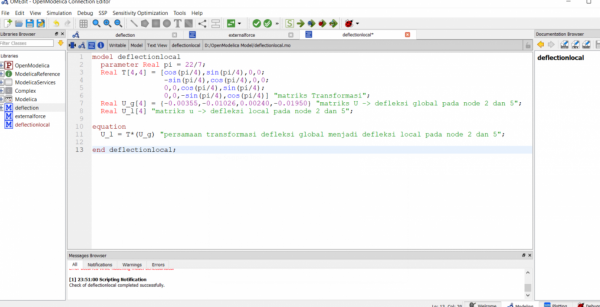
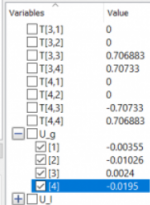
Pencarian deplacement/defleksi (u)
Pencarian gaya reaksi (R)
Perhitungan:
No.8
Pertemuan 5 (7 Desember 2020)
Pada pertemuan kali ini, Pak Dai memberikan tugas kepada kami sebagai berikut:
- Mempelajari codingan 3d fahmi
- Mengaplikasikan pada soal example 3.3
- Memberikan masukan atas codingan Fahmi
Jawab:
| No.4 | No.8 |
|---|---|
1. Class 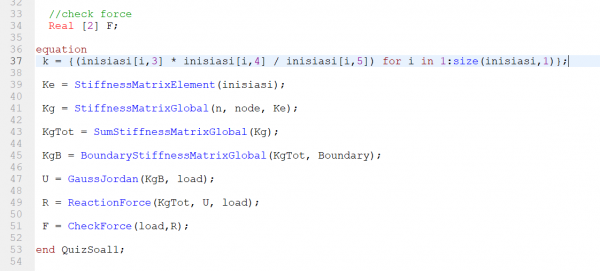 |
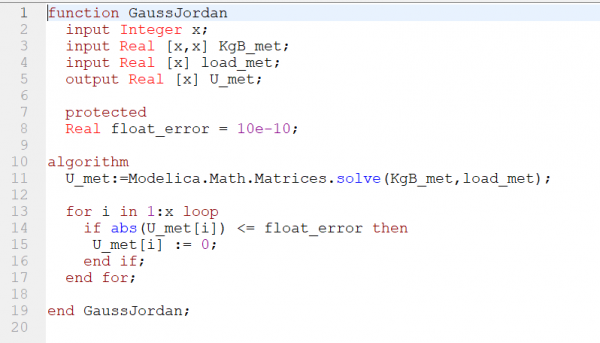
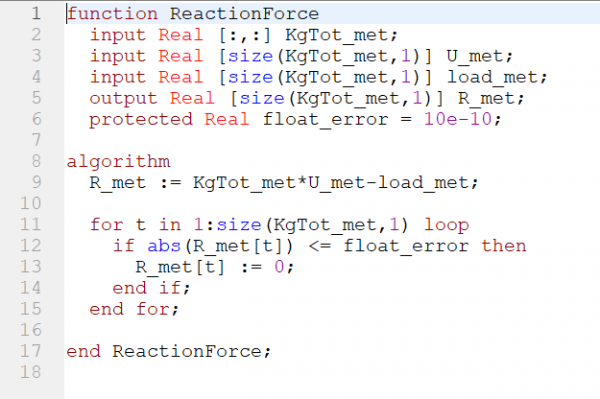
1. Class 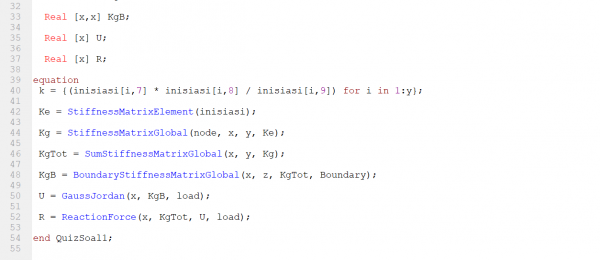
|
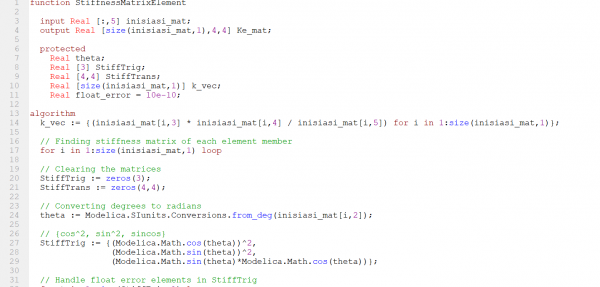 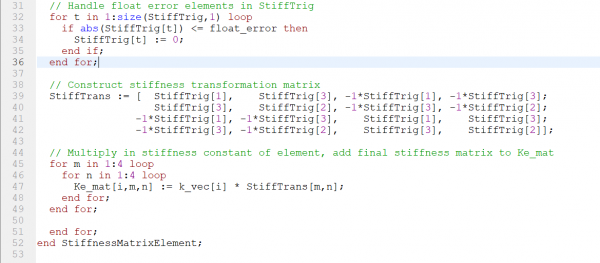 |
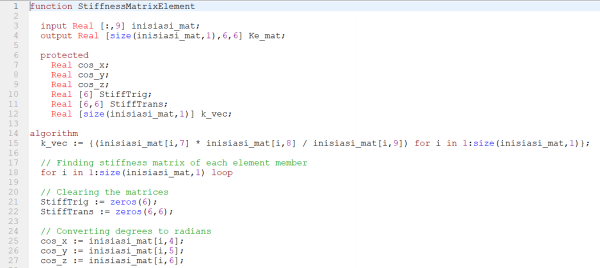 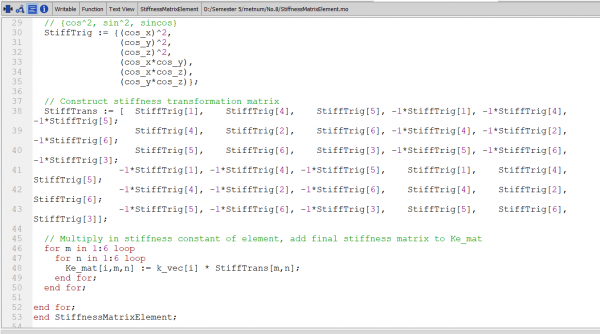
|
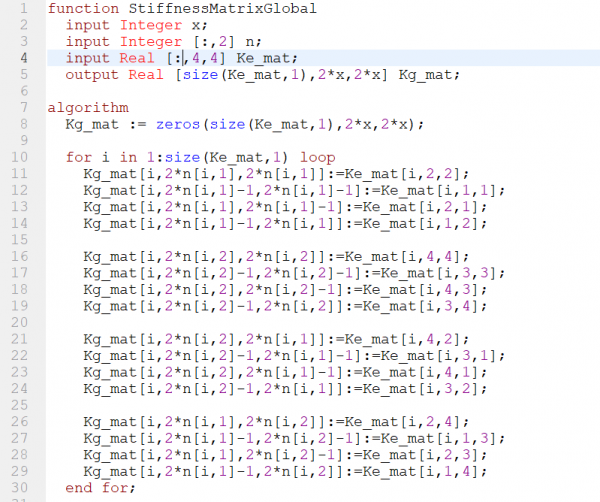  |
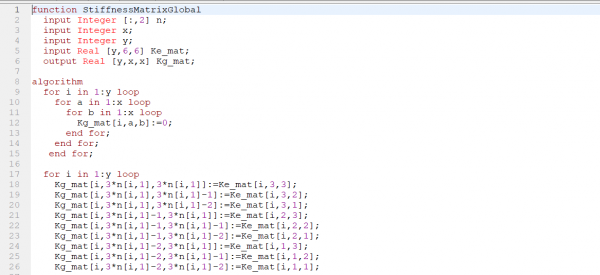 
|
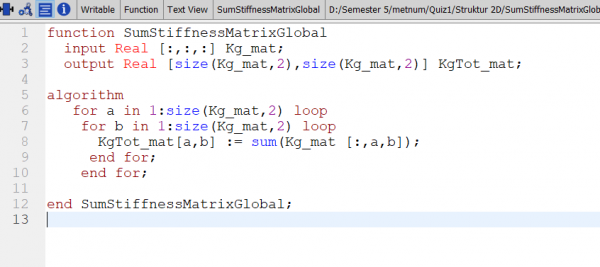 |
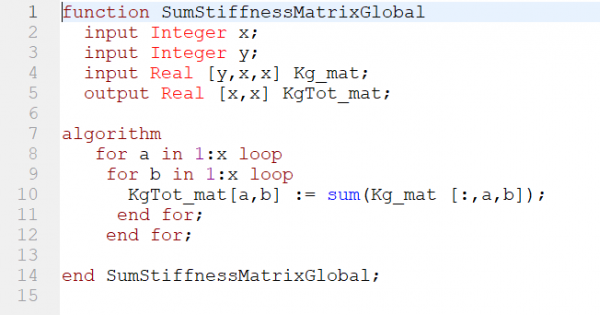
|
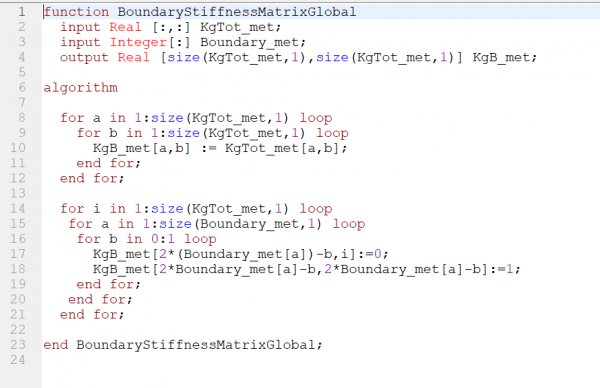 |
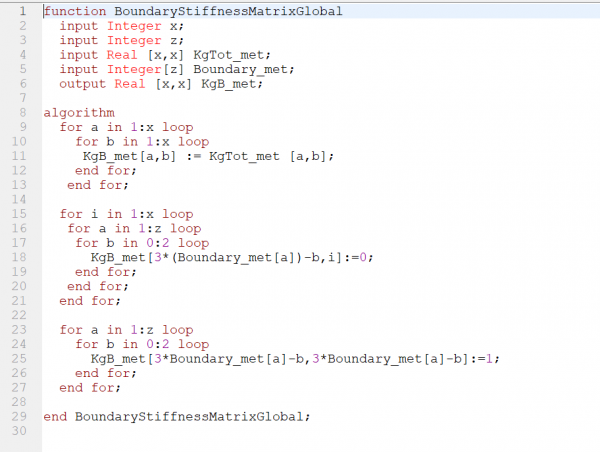
|
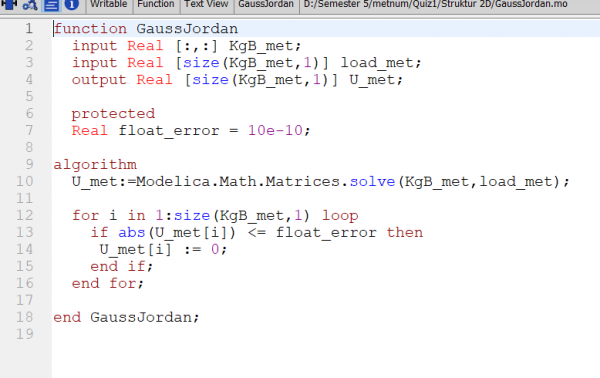 |
|
 |

|
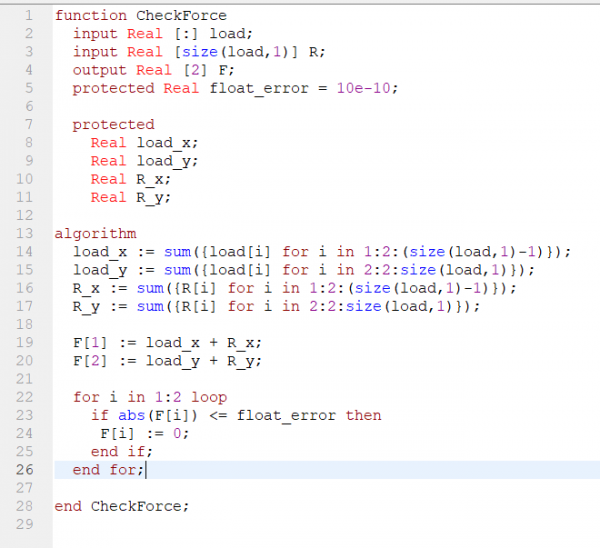
|
Pada pengerjaan di atas, masih terdapat kekurangan dimana kita masih kurang memaksimalkan komputerisasi. Perhitungan panjang batang dan besar nilai theta masih secara manual. Kita seharusnya dapat menggunakan koordinat untuk mendapatkan nilai-nilai tersebut seperti coding struktur 3D berikut ini untuk soal example 3.3 pada tautan berikut:
https://drive.google.com/drive/folders/1X05i3a90TrB4vbeqcaCUyqnfwgWlEqTC?usp=sharing
Pertemuan 6 (14 Desember 2020)
Pada pertemuan kali ini, Pak Dai mempersilahkan semua mahasiswa melakukan muhasabah untuk menilai sendiri pemahaman masing-masing untuk algoritma dan penerapannya (encoding modelica) untuk aplikasi metoda numerik dalam kasus statika struktur statis Truss 2D (bodang) dan 3D (Space).
Saya termasuk yang diberikan kesempatan untuk memaparkan hal tersebut di kelas. Saya mencoba untuk mengevaluasi pemahaman konsep dan pengalaman yang telah saya dapatkan selama pembelajaran mata kuliah Metode Numerik. Selain evaluasi yang sudah saya paparkan, saya juga ingin membagikan pengalaman kontribusi kecil saya di kelas ini. Saya diberikan kesempatan oleh Fahmi untuk mereview program yang sudah dibuat oleh Fahmi untuk topik Trusses, dan recordnya dibagikan kepada teman-teman. Disini saya juga berusaha untuk belajar memaparkan seinformatif mungkin agar dapat menjadi bekal saya apabila diminta untuk menjelaskan di kelas bersama Pak Dai.
Pada kelas ini, Pak Dai juga mengundang mahasiswa dari kelas reguler sehingga dilanjutkan dengan diskusi singkat mengenai materi yang telah diberikan selama ini. Pak Dai memberikan arahan mengenai tugas besar yang bertemakan aplikasi metoda numerik dalam optimasi statika struktur space truss (3d) untuk dikumpulkan di wiki 1 minggu sebelum UAS
Pertemuan 7 (21 Desember 2020)
Tugas Besar: Aplikasi Metoda Numerik dalam Optimasi Statika Struktur Rangka Sederhana space truss (3D)
Arahan dari Pak Dai adalah kelas bekerja sama untuk membuat suatu program bersama untuk mencari optimisasi desain untuk menekan biaya pada kasus yang diberikan. Optimisasi adalah suatu cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Dalam optimisasi tersebut harus ada fungsi objektif dan ada konstrain/batasan/interval. Diskusi kelas telah dilaksanakan sebanyak 2 kali
PENGERJAAN
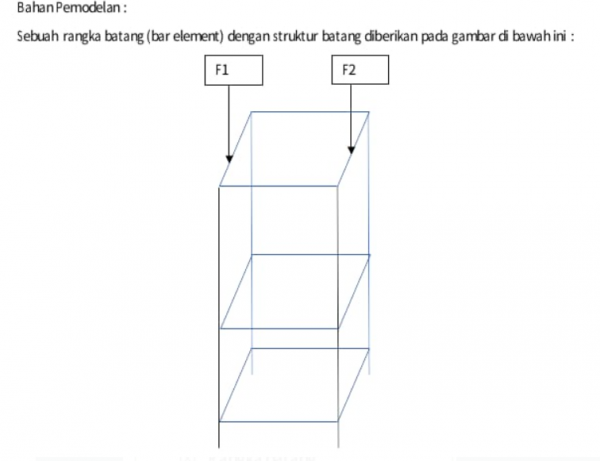
Profil truss siku:
Konstrain:
- Spesifikasi L (Panjang) dan geometri rangka truss
- Gaya beban terhadap struktur (1000 N dan 2000 N)
Tujuan
Mengoptimalkan desain rangka dan biaya dengan variasi dimensi dan elastisitas material.
Asumsi
- Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
Data Hasil
Pencarian Data Material
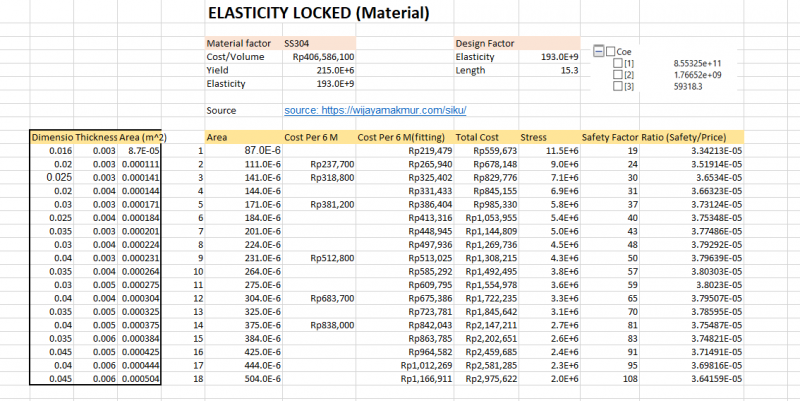
Untuk nilai elastisitas/material yang sama, langkahnya sebagai berikut:
- Mencari data yield strength dan elasticity dari material yang dipilih
- Mencari harga truss sesuai dengan material.
- Menghitung nilai safety factor.
- Membuat rasio (efficiency) dari safety factor dengan total cost.
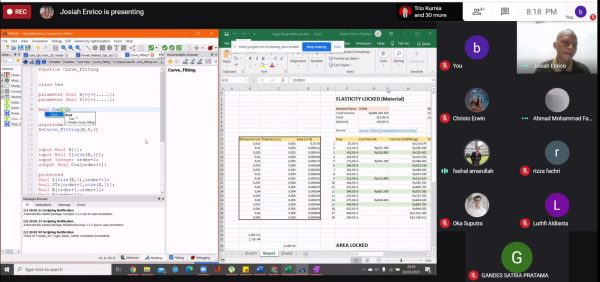
- Membuat persamaan (mencari Coe) antara rasio dengan area menggunakan curve-fitting.
- Melakukan optimasi menggunakan metode golden section.
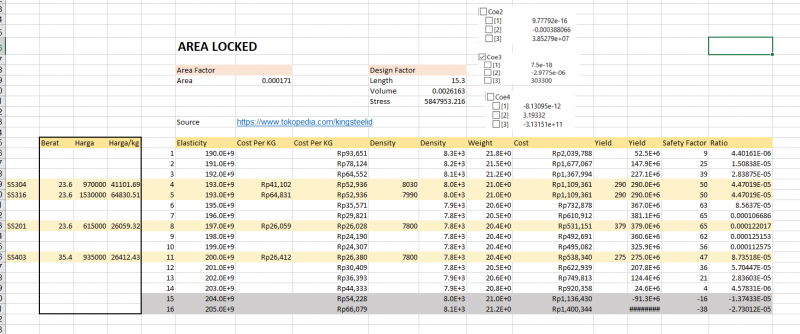
Untuk luas penampang yang sama, langkahnya sebagai berikut:
- Mendefinisikan luas penampang yang sama untuk seluruh variasi material.
- Mencari harga untuk 3 jenis variasi material.
- Menghitung nilai safety factor pada 3 variasi truss.
- Membuat rasio antara safety factor dengan total cost.
- Membuat persamaan (mencari Coe) antara rasio dengan area menggunakan curve-fitting.
- Melakukan optimasi menggunakan metode golden section.
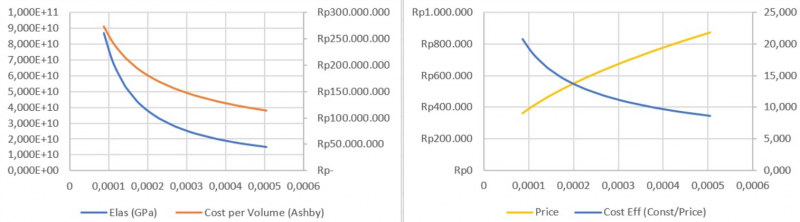
Lewat perhitungan numerik curve-fitting function, kita memperoleh sebuah kelompok koefisien yang membentuk kurva untuk kolom cost per 6 m
Lewat perhitungan numerik curve-fitting function, kita memperoleh 3 kelompok koefisien yang membentuk kurva untuk kolom masing-masing cost per kg, density, dan pada yield.
Kode Modelica Pendukung
|
Trusses Modelling
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
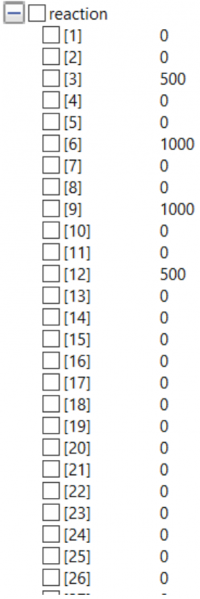
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
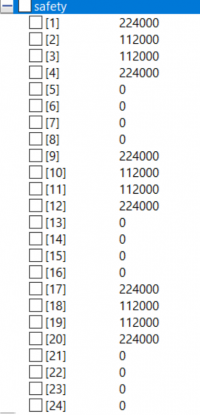
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
|
Referensi
https://duniabahanbangunanbandung.blogspot.com/p/harga-besi-siku-stainless-steel.html
http://www.wermac.org/steel/dim_angle_eq.html
https://wijayamakmur.com/siku/
https://www.tokopedia.com/aalt-co/siku-aluminium-30x30x3-pjg-6000mm
Pertemuan 8 (4 Januari 2020)
Pada oertemuan kali ini, dilaksanakan verifikasi oleh Pak Dai atas muhasabah yang telah dilakukan oleh masing-masing mahasiswa.
1. Value (adab/attitude/moral value seperti tingkat kerajinan (kehadiran, menulis (tugas wiki), ketekunan, kesungguhan, dll)
2. Pemahaman pengetahuan/ knowledge (konsep-konsep dan prinsip-prinsip metoda numerik)
3. Keterampilan (skill dlm mengaplikasikan konsep dalam penyelesaian kasus (algoritma, pemrograman, dll)
UAS
Nomor 1
Nomor 2
Nomor 3
Nomor 4,5 & 6
Nomor 7
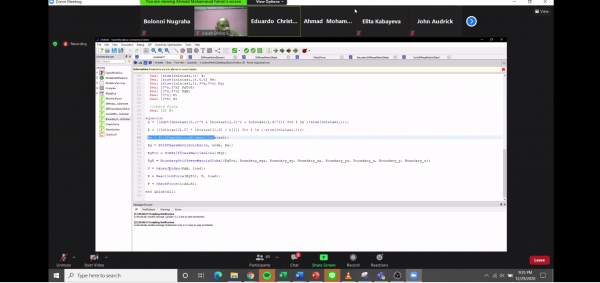
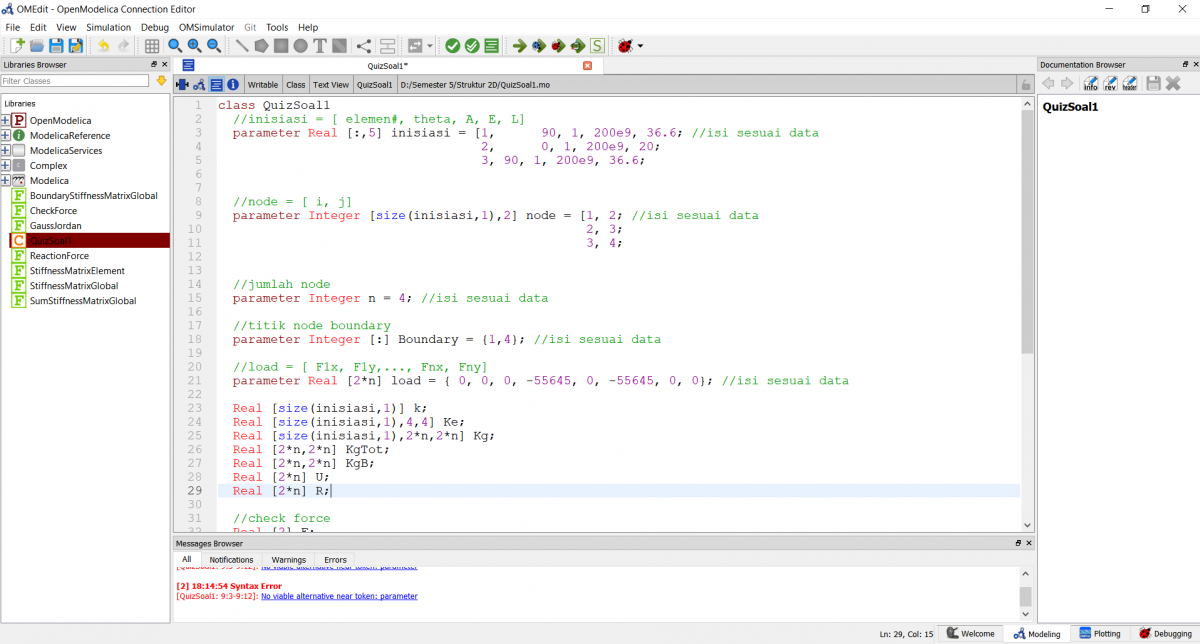
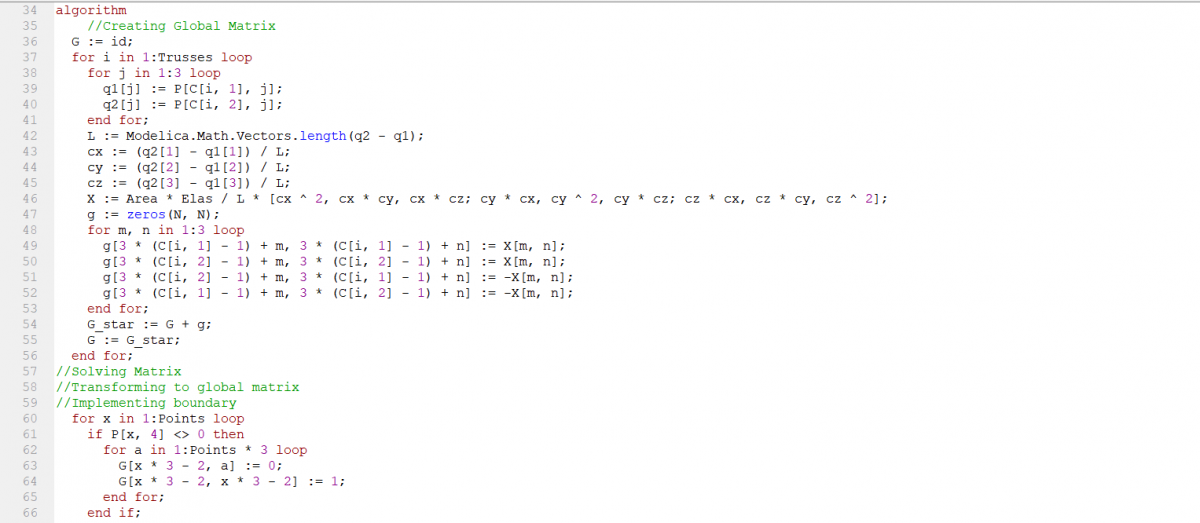
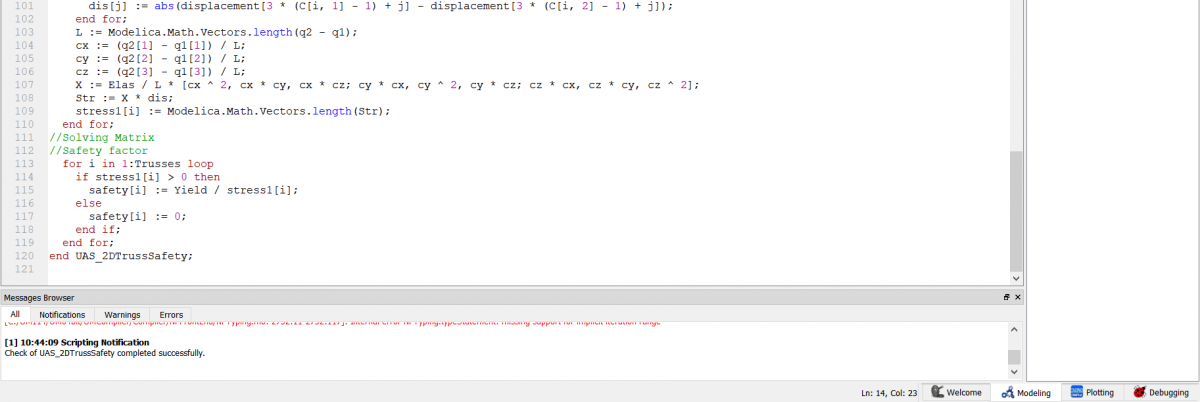
Saya menggunakan program yang dibuat oleh Fahmi sewaktu penyelesaian example 3.3 (Quiz) diatas sebelumnya. Namun, nilai-nilai yang dicari tidak berhasil didapat karena ditemukan error. Dokumentasinya adalah sebagai berikut.
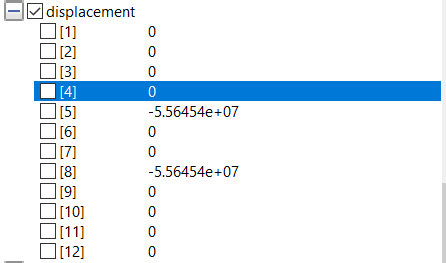
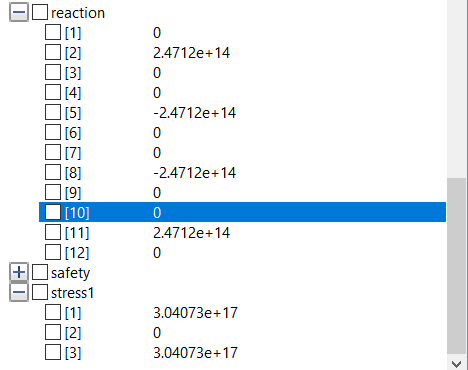
Kemudian, saya berusaha untuk memperbaiki jawaban ini agar dapat menjadi bahan evaluasi saya berikutnya. Dengan nilai-nilai parameter input yang saya coba sesuaikan dengan ketersediaan bahan di lapangan dan diskusi saya dengan seorang ahli di bidang struktur (ayah saya), saya mencoba untuk mensimulasikannya dengan program yang dibuat oleh teman saya. Berikut adalah dokumentasinya.
Brikut adalah nilai-nilai hasil simulasi yang didapatkan