Fashal Firdaus Amarullah
| Profile | |
|---|---|
| Nama Lengkap | Fashal Firdaus Amarullah |
| NPM | 1906301186 |
| Jurusan | Teknik Mesin |
| Alamat Surel | fashalamarullah@gmail.com |
Nama saya adalah Fashal Firdaus Amarullah sebagai mahasiswa Teknik Mesin angkatan 2019 dan saya adalah salah satu ciptaan terbaik dari Tuhan Yang Maha Esa karena pada prinsipnya Tuhan Yang Maha Esa itu mendesain manusia dengan sebaik-baiknya makhluk. Pada kali ini saya sedang belajar mata kuliah metode numerik. Sebagai mahasiswa saya juga aktif dibeberapa lembaga dan kepanitiaan yang ada di Fakultas Teknik Universitas Indonesia. Saya mengikuti organisasi IMM FTUI sebagai Badan Pengurus bidang Litbang IMM FTUI 2020. Di departemen saya juga aktif di KPD HTW sebagai member. Dilingkup Fakultas Teknik saya menjadi Badan pengurus bidang Relasi BEM FTUI 2020. Saya juga aktif dalam kepanitiaan lingkup Fakultas Teknik sebagai Vice Project Officer Aksioma FTUI 2020 yang merupakan acara tahunan fakultas teknik dalam bidang sosial masyarakat.
Contents
Metode Numerik
Metode numerik adalah metode penyelesaian masalah yang diformulasikan secara matematis dengan menggunakan operasi hitungan yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan yang tidak dapat diselesaikan menggunakan metode analitik. Metode numerik dapat memecahkan suatu permasalahan menggunakan pendekatan-pendekatan yang bersifat analitik. Biasanya hasil dari perhitungan metode numerik bersifat berupa hampiran atau pendekatan.
Pertemuan Minggu Pertama (11 November 2020)
Saat pertemuan pertama kali ini kami diajarkan oleh Bapak Dr. Ir. Ahmad Indra Siswantara tentang tujuan dari pembelajaran metode numerik,diantaranya:
1. Dapat memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik seperti:persamaan diferensial parsial, Persamaan algoritma, pencocokan kurva,aljabar, dan lainnya
2. Dapat menerapkan metode numerik dalam hal terkait persoalan keteknikan
3. Dapat mengerti dan mampu menerapkan pemahaman atau aplikasi terhadap konsep metode numerik
4. Mendapat nilai tambah atau adab sehingga kita menjadi orang yang lebih beradab
Pada pertemuan pertama ini, kami juga diajarkan tentang penggunaan software Open modelica. Selain itu beliau juga banyak mengajarkan tentang nilai-nilai kebaikan dalam kehidupan.
Tugas Minggu Pertama
Pada tugas pertama kami diberikan tugas untuk mempalajari penggunaan software Open Modelica, yaitu sebuah sofware untuk membuat sebuah simulasi dan modelling. Open Modelica biasanya digunakan untuk perhitungan industri pada pabrik dan juga biasa digunakan untuk pemecahan masalah metode numerik. Disini beberapa contoh dari youtobe yang saya sudah tonton:
- https://www.youtube.com/watch?v=m0Ahs8fEN28&ab_channel=NSTUFACE
- https://www.youtube.com/watch?v=GhtBMIlO70w&ab_channel=Processdynamicsandcontrol
Selain itu kami juga disuruh membuat sebuah video tutorial penggunaan software open modelica. Berikut video tutorial yang saya buat:
Pertemuan Minggu Kedua (18 November 2020)
Pada pertemuan kedua kali ini, diawali dengan pesan-pesan kehidupan dari Pak Dai. Beliau memberikan saran agar sebagai manusia kita harus terus berkembang setiap harinya dan menjadi lebih baik dari hari ke hari. Pada minggu ini, banyak mereview tentang tugas yang diberikan pada minggu lalu yaitu penggunaan software Open Modelica. Banyak teman-teman kelas yang mempresentasikan tentang tugas mereka pada minggu lalu. Selain itu Pak Dai juga menjelasakan kelebihan dari Software Open MOdelica. Pada Software ini mempunyai fitur-fitur untuk membuat function, model, persamaan, dlll. Software Open Modelica juga dapat digunakan secara free sehingga dapat digunakan oleh semua orang.
Pada Pertemuan kedua kali ini kami juga diajarkan menggunakan open modelica untuk menggabungkan function kedalam class yang sudah dibuat. Setelah kami diajarkan,kemudian saya mencobanya dengan open modelica. Berikut tahapan-tahapannya:
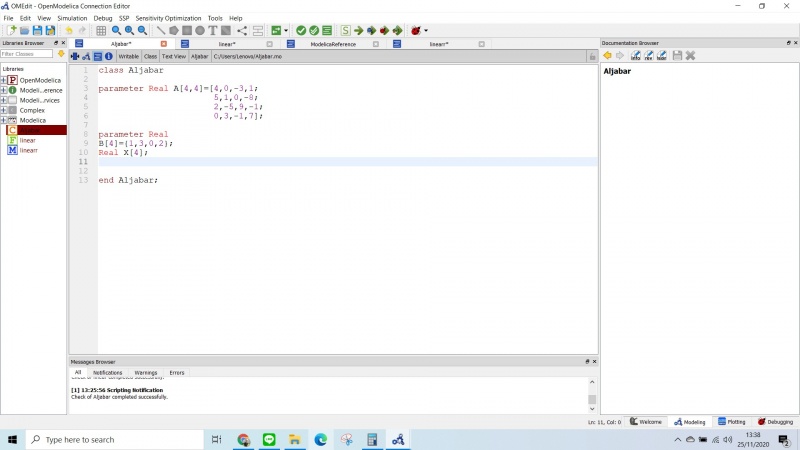
- 1. Buatlah class baru dengan menggunakan open modelica seperti berikut
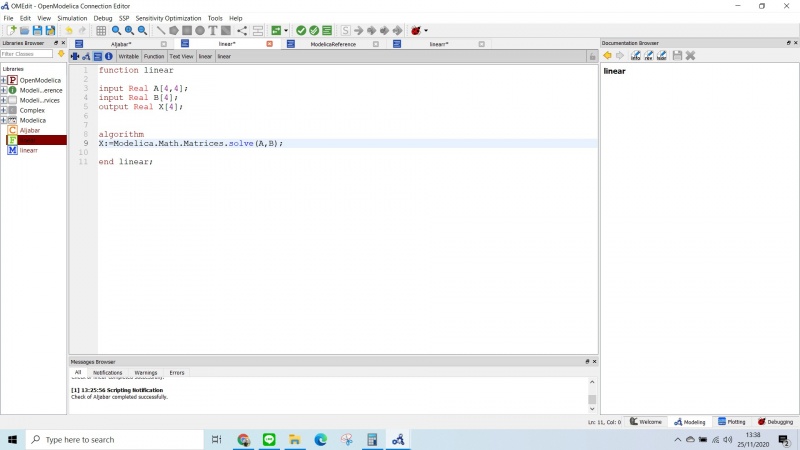
- 2. Setelah itu buatlah function baru seperti pada gambar berikut
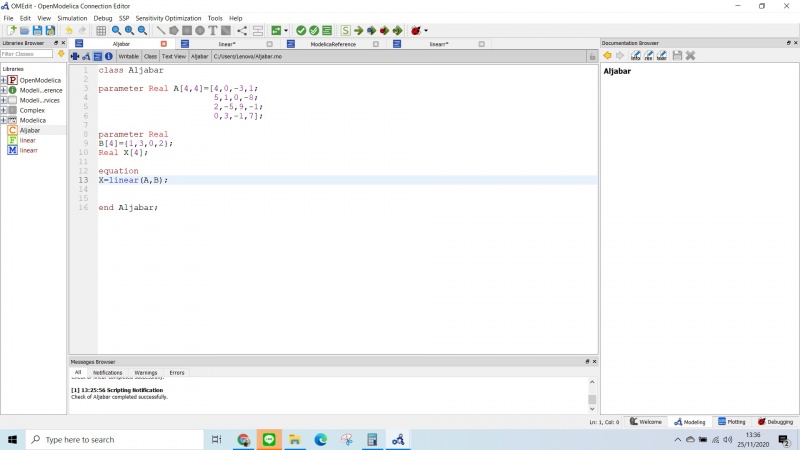
- 3. Setelah selesai membuat function , kembali lagi kehalaman class, dan tarik function ke class menggunakan cara seperti digambar
Tugas Minggu Kedua
Pada Tugas Minggu kedua ini, kami ditugaskan untuk mempelajari penggunaan Open Modelica untuk penyelesaian Aljabar. Berikut Video Tutorial yang saya buat:
Pertemuan Minggu Ketiga (25 November 2020)
Pada pertemuan ketiga kali ini kami membahas tentang penggunaan Open Modelica pada permasalahan engineering. Pada permasalahan engineering, metode numerik dapat membantu menyelesaikan persoalan agar lebih cepat. Beberapa contoh metode numerik yang dapat membantu menyelesaikan permasalaha engineering diantaranya CFD(Computation fluid dynamics, Metode Stokastik, dan FEA ( FInite Element Analaysis). Tahapan untuk menyelesaikan masalah engineering menggunakan metode numerik:
- 1. Melakukan analisis terhadap masalah engineering
- 2. Melakukan pemodelan matematis dari masalah yang sudah dianalisis
- 3. Menerjemahkan pemodelan matematis yang sudah dibuat menjadi metode numerik agar bisa dhitung oleh komputer
- 4. Melakukan perhitungan metode numerik menggunakan software dan dihasilkanlah solusi dari masalah engineering tersebut
CFD Simulation
Computational fluid dynamics ( CFD ) adalah cabang dari mekanika fluida yang menggunakan analisis metode numerik dan struktur data untuk menganalisis dan memecahkan masalah yang melibatkan aliran fluida. Dasar fundamental dari hampir semua masalah CFD adalah persamaan Navier-Stokes , yang mendefinisikan banyak aliran fluida pada satu fasa. Persamaan-persamaan ini dapat disederhanakan dengan menghilangkan suku-suku yang mendeskripsikan tindakan kental untuk menghasilkan persamaan Euler . Penyederhanaan lebih lanjut, dengan menghilangkan istilah yang menggambarkan vortisitas menghasilkan persamaan potensial penuh.
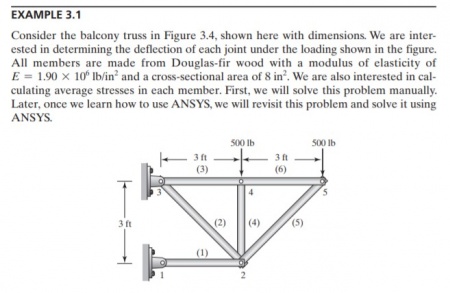
Finite Element Method for Trusses
The finite element method (FEM) is a numerical technique used to perform finite element analysis (FEA) of any given physical phenomenon. It is necessary to use mathematics to comprehensively understand and quantify any physical phenomena, such as structural or fluid behavior, thermal transport, wave propagation, and the growth of biological cells. Most of these processes are described using partial differential equations (PDEs). However, for a computer to solve these PDEs, numerical techniques have been developed over the last few decades and one of the most prominent today is the finite element method.
Example for trusses
We can use Finete Element Method to solve this problem. We can make equation with numerical method use Open modelica.
|
Persamaan model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses;
|
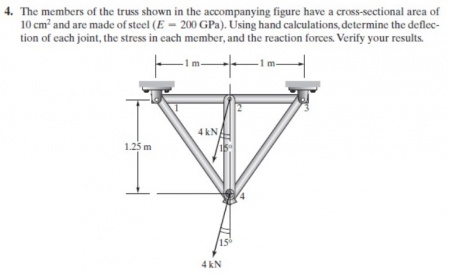
Trusses Problem 2 (Homework)
|
Persamaan class Trusses_HW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_HW;
|
Fungsi Panggil
|
Matrice Transformation function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
|
Global Element Matrice function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
|
Gauss_Jordan function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan; |
Reaction Matrice Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; |
Pertemuan 4 (02/12/2020)
Kita harus mengetahui hal apa saja yang akan kita lakukan
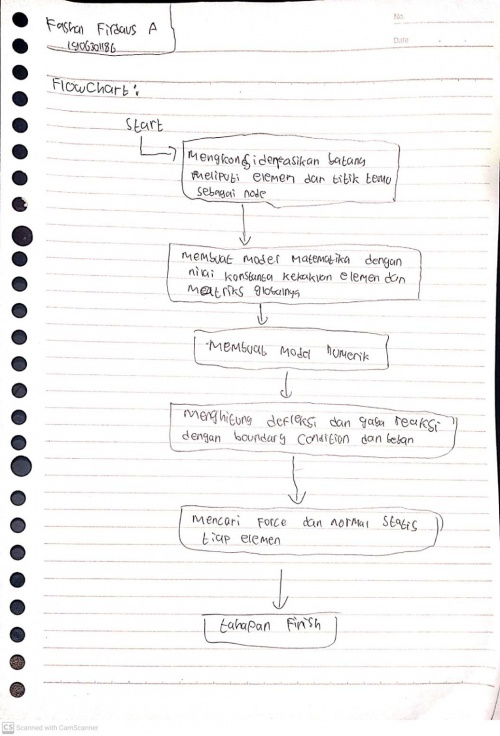
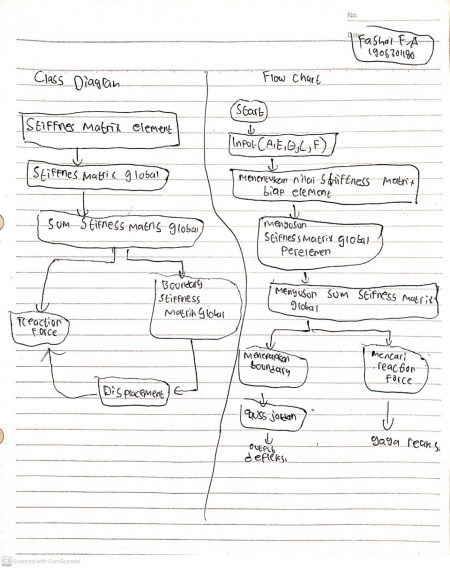
Quiz Diagram Class dan Flow Chart
Membuat flow chart dan class diagram dari coding trusse problem
Setelah memahami pembahasan,saya menggunakan 5 kelas. Ketika kita menggunakan matrices transfromation, kita ada menambahkan data sudut dari elemen pada truss, kemudia outputnya pun berupa matriks lokal dari kekakuan pegas. ketika persamaan global element matrice didapat, tiap matriks lokal kekukan elemen akan diletkannan dalam susunan matriks global. Didalam class truss berikutnya matriks tiap elemen diolah dengan luas penampang , modulus elastisitaas dan panjang tiap elemen, yang selanjutnya digabungkan menjadi suatu matriks global g, dengan penerapan boundary conditon, selanjutnya diselesaikan dengan gauss jordan untuk mendapatkan nili defleksi dan digunakanlah fungsu reaction untuk menghasilkan gaya reaksi.
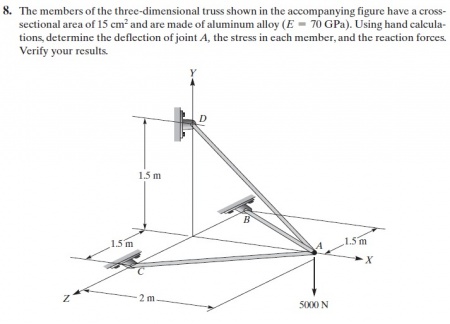
Buatlah Flowchart untuk soal berikut
Pembuatan Flowchart
perhitunganflow chart
Tugas Minggu IV
Mebuat flow chart diagram class dan coding open modelica
Pada langkah pertama saya membuat class diagram dan flowchart untuk tugas ini
Saya membuat FBD untuk mencari data-data yang diperlukan, yaitu node, sudut, luas, modulus elastisitas, dan panjang dari tiap batang. Karena ini merupakan permasalahan 3D, maka sudut akan ada pada arah x, y, dan z.
StiffnessMatrixElement
function StiffnessMatrixElement
input Real [:,9] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real cos_z;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
// Converting degrees to radians
cos_x := inisiasi_mat[i,4];
cos_y := inisiasi_mat[i,5];
cos_z := inisiasi_mat[i,6];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
Setelah itu dibuat matriks K global 12x12 dari tiap element
StiffnessMatrixGlobal
function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal;
Setelah itu semua matriks global dari tiap element akan dijumlahkan
SumStiffnessMatrixGlobal
function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
Setelah itu tentukan juga boundariesnya
BoundaryStiffnessMatrixGlobal
function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
end BoundaryStiffnessMatrixGlobal;
Untuk mencari displacement-nya digunakan gauss jordan untuk menyelesaikan matriks
GaussJordan
function GaussJordan
input Integer x;
input Real [x,x] KgB_met;
input Real [x] load_met;
output Real [x] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
Dan untuk melihat reaction nya digunakan code sebagai berikut :
ReactionForce.mo function ReactionForce input Integer x; input Real [x,x] KgTot_met; input Real [x] U_met; input Real [x] load_met; output Real [x] R_met; algorithm R_met := (KgTot_met*U_met)-load_met; end ReactionForce;
Terakhir dibuat Class untuk memproses data yang sudah dibuat dan melihat hasil U dan R
QuizSoal1
class QuizSoal1
parameter Real [:,9] inisiasi = [1, 1, 2, -0.8, 0, -0.6, 15e-4, 70e9, 2.5;
2, 1, 3, -0.8, -0.6, 0, 15e-4, 70e9, 2.5;
3, 1, 4, -0.8, 0, 0.6, 15e-4, 70e9, 2.5];
parameter Integer [:,2] node = [1, 2;
1, 3;
1, 4];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {2,3,4};
parameter Real [:,4] node_load = [1, 0, -5000, 0;
2, 0, 0, 0;
3, 0, 0, 0;
4, 0, 0, 0];
parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = StiffnessMatrixElement(inisiasi);
Kg = StiffnessMatrixGlobal(node, x, y, Ke);
KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
U = GaussJordan(x, KgB, load);
R = ReactionForce(x, KgTot, U, load);
end QuizSoal1;
Berikut video tutorial mencari defleksi trusses 3d yang saya buat :
Pertemuan Minggu 5 : Kelas Pengganti
Pada pertemuan kelas pengganti ini, kami mereview ulang hal apa saja yang sudah adad pada pertemuan sebelumnya. Pada kelas ini kami juga diajarkan kembali tentang sistem trusses menggunakan software open modelica. Pak Dai sebagai dosen metnum juga mengajarkan tentang pelajaran-pelajaran hidup. Beliau banyak memberikan nasihat-nasihat kebaikan pada kehidupan seperti manusia yang harus selalu berserah diri kepada Allah SWt. Beliau juga mengajarkan kita untuk muhasabah diri dengan memberi penilaian kepada diri sendiri tentang kemampuan penguasaan materi trusses menggunakan Open Modelica.
Pertemuan Minggu 6
Pada pertemuan kali ini kami diajarkan tentang optimasi menggunakan Open Modelica. Optimasi sendiri adalah sebuah cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan. Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada kali ini Asisten Dosen yaitu Bu Chandra memberikan tutorial untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu graik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan sampai melakukan optimasi grafik tanpa sebuah konstrain.
Selanjutkan Bu Chandra mengajarkan langsung, dengan menggunakan Software Open MOdelica. Kita dapat membuat sebuah fungsi pada awalnya:
Fungsi panggil
function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:= 2*Math.sin(x)-x^2/10; end f_obj3;
setelah itu kita dapat membuat model optimasi sistem bracket sesuai yang diajarkan
model bracket_optimation3 parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt; algorithm xup :=4; xlow:=0; for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= f_obj3(x1[i]); f2[i]:= f_obj3(x2[i]); if f1[i]>f2[i] then xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; end bracket_optimation3;
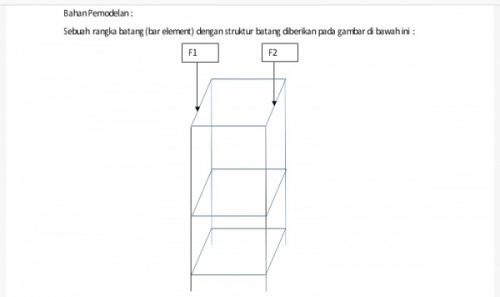
Sinopsis Tugas Besar : Aplikasi Metode Numerik dalam Optimasi Design Struktur Rangka Sederhana
Pada tugas besar kali ini kita akan mendesign suatu rangka dengan cost yang yang serendah mungkin tetapi dengan kualitas yang optimum. Terdapat beberapa variabel yang diperhatikan diantaranya :
- 1. Harga material
- 2. Jenis material
- 3. Luas Cross Section
- 4. Penampang yang digunakan
Setelah itu kita akan melakukan optimasi dan membentuk kurva efisiensi harga dengan curve fitting menggunakan Metode numerik.
Pada tugas besar trusses kali ini saya menggunakan asumsi:
- Area=0.000171
- Material yang digunakan adalah Steel SS201
Hasil Open modelica
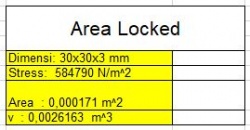
Pada proses pemodelan untuk rangka ini dilakukan menggunakan open modelica. pada pemodelan ini terdapat input yang kita sesuaikan yaitu parameter elstisitas,parameter luas penampang, dan bentuk design rangka. pada tahap berikutnya kita juga harus mendefiniskn point sambungan serta jumlah trusses, point dan jumlah sambungan pada design,lalu diperlukan juga elemen area berupa satuan luas. Berikutnya parameter elastisitas disesuaikan dengan material yang saya pkai yaitu SS201 dengan elastisitas 197,0E+9 N/m^2.
- Brikut Untuk perhitungan Reaction force, displacement, stress, dan safety factor:
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=379e6; //Yield Strength (Pa)
parameter Real Area=0.000171; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=197e9; //Elasticity SS 201 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
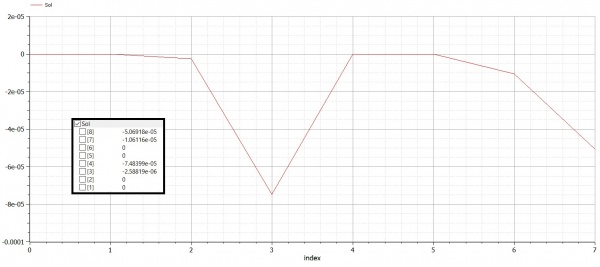
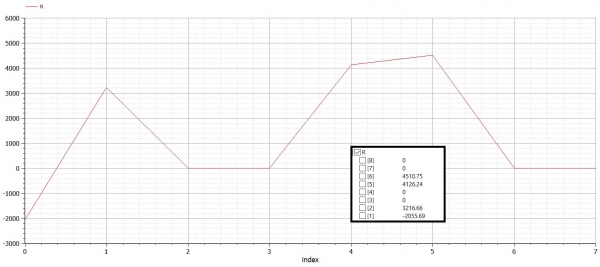
Pada hasil open modelica didapat nilai displacement dan reaction sebagai berikut :
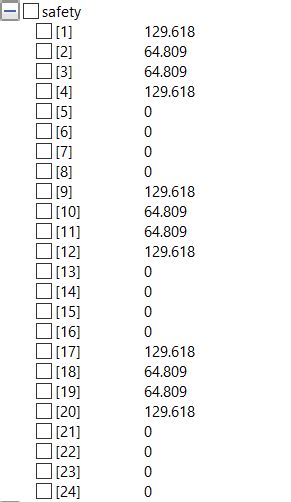
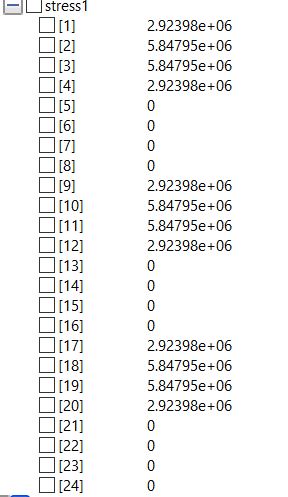
Lalu didapat juga hasil stress dan safety pada open modelica dan kita running satu persatu:
Pada saat melakukan optimasi kita menggunakan 2 metodologi yaitu:
Untuk jenis material yang sama:
- Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu s201.
- Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal.
- Membuat rasio antara safety factor dengan harga total.
- Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting.
Untuk area penampang yang sama:
- Mencari harga untuk 4 jenis material dengan area penampang yang sama yaitu 171 mm^2.
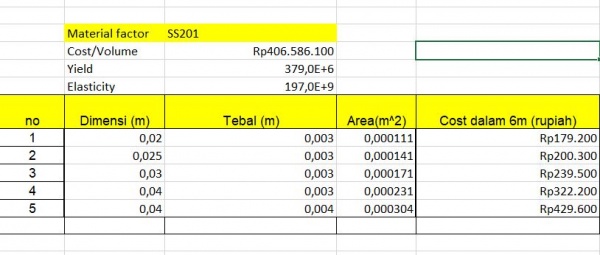
Untuk jenis material yang sama
Data yang dipakai adalah
Hasil perhitungan yang didapat adalah
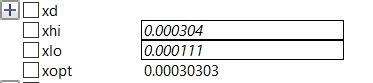
Kemudian kita gunakan open modelica untuk mengoptimasi data yang sudah didapat. pada kali ini saya menggunakan nilai minimum xlo= 0,000111 dan nilai maksimum xhi= 0.000304. Maka didapatlah hasil optimasi seperti berikut:
Dari hasil yang didapat , dapat disimpulkan bahwa dengan menggunkan material ss201 luas area yang optimum adalah dengan 303 mm^2.
Untuk area penampang yang sama
Data yang dipakai adalah
Hasil perhitungan yang didapat adalah
Kemudian kita gunakan open modelica untuk mengoptimasi data yang sudah didapat. pada kali ini saya menggunakan nilai minimum xlo=193e+11 dan nilai maksimum xhi= 200e+11. Maka didapatlah hasil optimasi seperti berikut:
Dari hasil yang didapat, dapat disimpulkan bahwa dengan luas area truss sebesar 171 mm^2 , material yang paling cocok untuk bahan dasar rangka adalah material stainless steel s201 dengan modulus elastisitas sebesar 1.93035x10^13 Pa