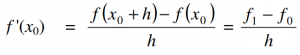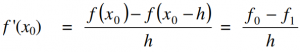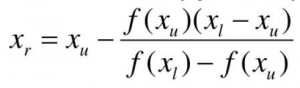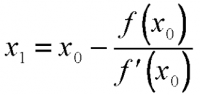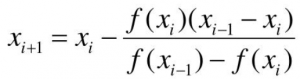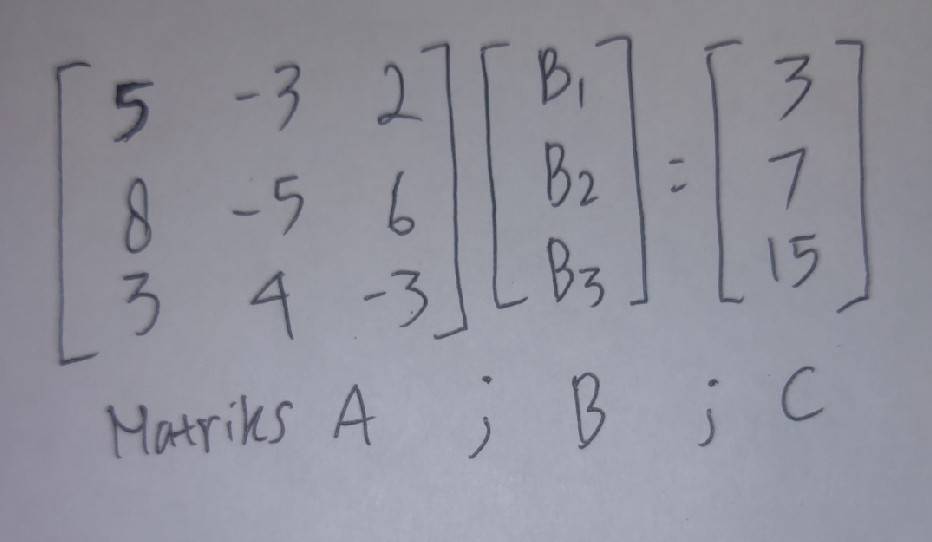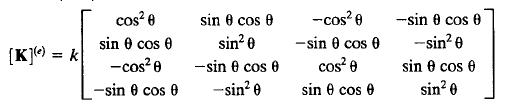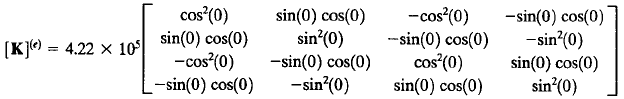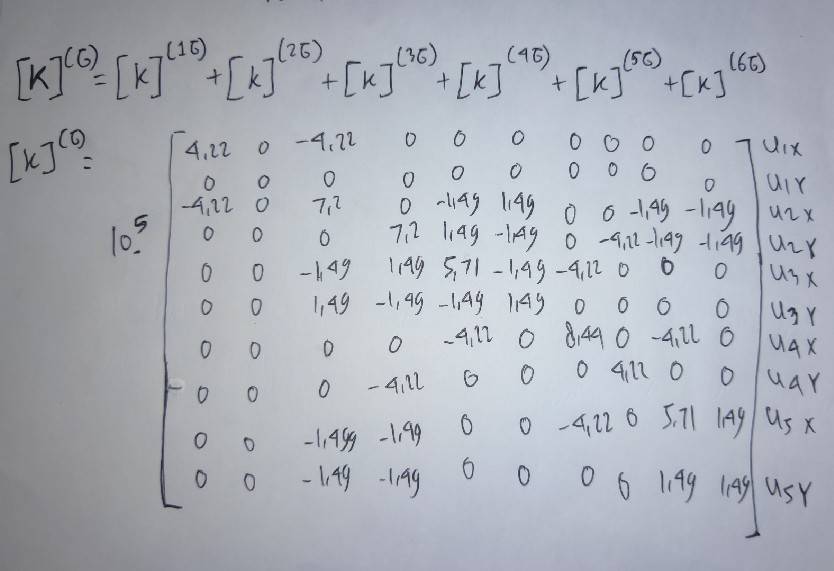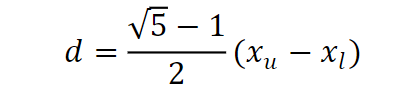Metnum03-Rizki Ramadhan
Contents
- 1 Biografi
- 2 Tugas 1 : Tutorial Open Modelica
- 3 Pertemuan Kedua, 16 November 2020
- 4 Tugas 2 : Mencari akar persamaan dengan metode gauss
- 5 Pertemuan Ketiga, 23 November 2020
- 6 Tugas 3: Menganalisis stress menggunakan openmodelica dengan segmentasi node
- 7 Pertemuan 4
- 8 Pertemuan 5
- 9 Pertemuan 6: Aplikasi Metode Numerik dalam kasus Optimasi
- 10 Pertemuan 7: Review progress tugas besar Optimasi trusses 3D
- 11 Tugas Besar Metode Numerik: Optimasi Trusses 3D
Biografi
Nama : Rizki Ramadhan Siregar
NPM : 1806233240
Tempat & Tanggal Lahir : Bengkulu, 4 Desember 2000
Jurusan : Teknik Mesin
Perkenalkan saya Rizki Ramadhan dari kota Bengkulu provinsi Bengkulu. Saat ini saya berkuliah di Universitas Indonesia Jurusan Teknik Mesin angkatan 2018. Saya memiliki ketertarikan yang tinggi terhadap perkembangan teknologi dan berorientasi terhadap masa depan. Berbekal Pengalaman dan pelajaran dalam dunia perkuliahan yang saya jalani saat ini, Insha Allah akan memberikan sebuah makna baru untuk kehidupan kedepan dan berguna bagi nusa dan bangsa (Aamiin)
Materi Sebelum UTS
Pada pertemuan sebelum UTS, kami telah belajar 3 materi utama, yaitu turunan numerik, mencari akar-akar, dan membaca pola.
1. Turunan Numerik
- turunan numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menentukan turunan:
- Turunan maju
- Turunan mundur
- Turunan pusat
2. Mencari Akar
- Pada materi ini, kami belajar cara mencari akar dengan metode numerik. Ada 2 cara dalam mengerjakannya, yaitu bracketing method dan open method.
- Bracketing method
- Bracketing method adalah metode mencari akar dengan cara menebak dua nilai, kemudian mengurung kedua nilai tersebut sehingga kita dapat menemukan akar-akar dari persamaan. Pada metode ini, ada beberapa cara penyelesaian, yaitu metode graphical, metode bisection, dan false-position.
- Metode Graphical
- Metode ini digunakan dengan cara membuat grafik fungsi dan melihat perpotongan sumbu horizontal atau sumbu x.
- Metode Bisection
- Metode ini dilakukan dengan cara membagi dua kurva yang diwakili oleh suatu titik yang nilainya dikalikan oleh nilai tertinggi dan yang terendah. Metode ini terus dilakukan hingga menemukan akar.
- False Position
- Metode ini mirip dengan bisection, namun bedanya untuk penentuan titik tengah menggunakan segitiga dari titik perpotongan kurva dengan garis yang ditentukan.
- Open Method
- Metode ini hanya menggunakan 1 titik sebagai acuan pertama untuk menemukan akar yang dicari. Open method terbagi menjadi 3 cara, yaitu newton rhapson, secant, dan simple fix point.
- Newton Rhapson
- Metode ini dilakukan dengan cara menentukan suatu titik dan menarik garis singgung terhadap kurva. Cara menentukan garis singgung tersebut dengan turunan.
- Secant
- Metode ini mirip dengan Newton Rhapson, tapi estimasi dengan 2 titik jika pada newton rhapson f'(x) tidak dapat dicari.
- Simple Fix Point
- Metode ini menghitung seluruh kemungkinan x yang dihasilkan dan dicari x konvergen sehingga x=g(x).
3. Membaca Pola
- Ada dua cara dalam membaca pola suatu data, yaitu dengan regresi dan interpolasi
- Regresi
- Interpolasi
Tugas 1 : Tutorial Open Modelica
Pada Tugas pertama metode numerik ini, kami diperkenalkan sebuah aplikasi open source yaitu open modelica. Aplikasi ini berguna untuk menjalankan simulasi, plotting dan serta modelling. Untuk mendownload aplikasi open modelica yaitu pada website https://www.openmodelica.org/download/download-windows.
Pada tutorial ini saya mencoba untuk mensimulasikan persamaan pendulum untuk mengetahui sudut dan kecepatan sudut dari pendulum tersebut. langkah-langkahny seperti dibawah:
1.Buka aplikasi openModelica,klik pada menu new file dan masukkan nama file yang ingin dinamai
2.Setelah itu,klik pada text view sehingga tampilan seperti gambar dibawah
3. Setelah itu masukkan variabel-variabel dari persamaan yang akan diselesaikan. Variabel yang saya pakai ada beberapa yaitu g (percepatan gravitasi),L(panjang tali pendulum),Phi (sudut antara titik seimbang dan simpangan), serta w (kecepatan sudut pendulum)
4.Masukkan persamaan yang ingin diselesaikan pada kolom equation
5.Setelah semuanya sudah diinput seperti pada gambar
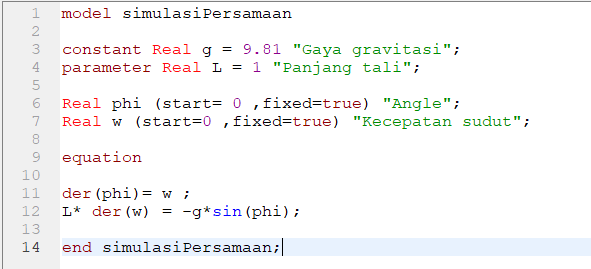
6.Setelah itu mulai simulasi dengan menetapkan stop time yaitu 5 sekon
7.Setelah itu mulai simulasi dan buka pada kolom plotting
8.Akan didapat grafik sudut dan kecepatan sudut seperti pada gambar dibawah
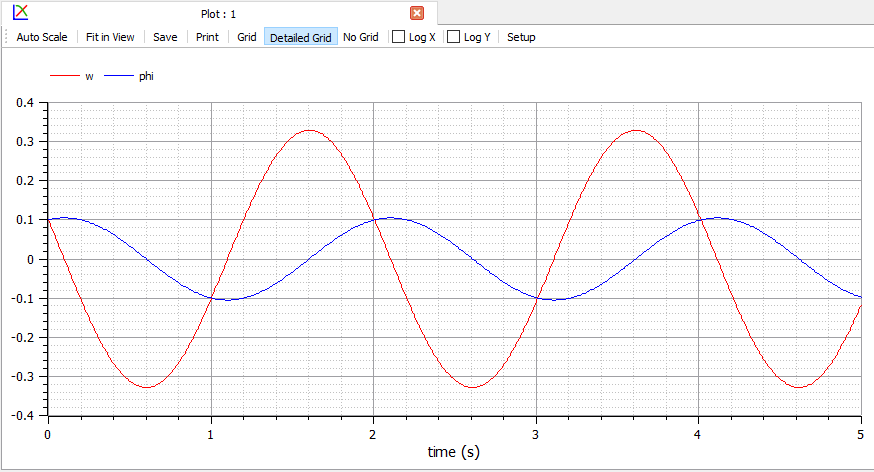
Untuk video tutorial bisa diakses pada link berikut : https://youtu.be/H6rh5GmI4Uw
Pertemuan Kedua, 16 November 2020
Pada pertemuan kedua,pak dai meminta mahasiswa untuk mencoba open modelica untuk menyelesaikan persamaan-persamaan sederhana seperti persamaan linier dan mencari rata-rata.
untuk menginput variabel parameter, dapat menginput Parameter real var
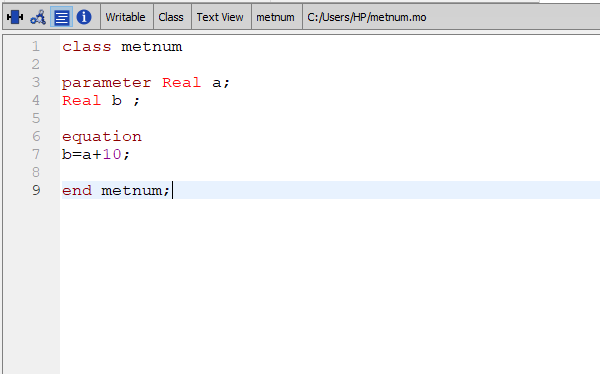
untuk menginput variabel biasa ,dapat menginput real var
sehingga untuk menyelesaikan persamaan b = a+10 dapat dituliskan seperti gambar
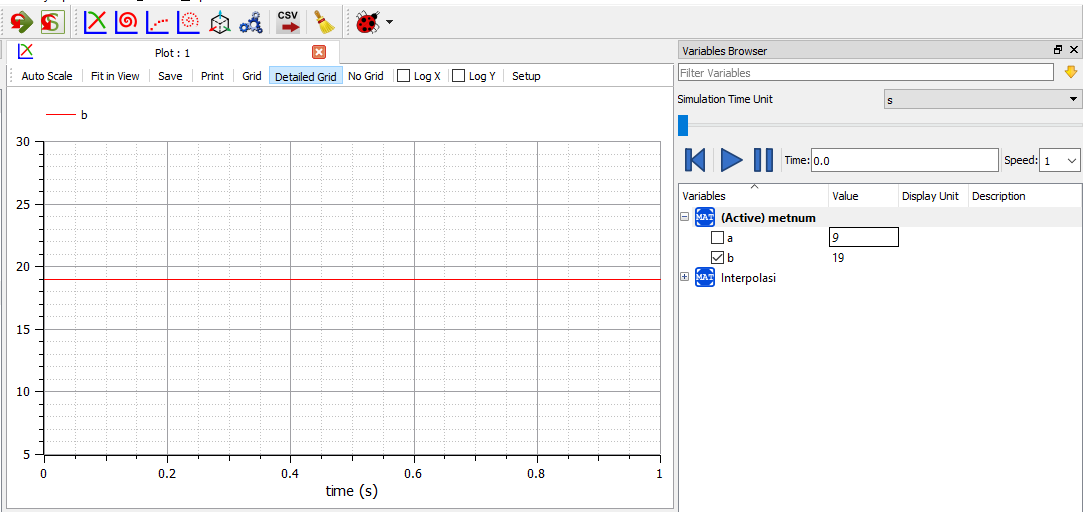
setelah diinput semua codingan,maka langsung jalankan simulasi dan diperoleh hasil seperti digambar
pada kolom plotting maka kita bisa merubah variabel a dan kita akan memperoleh variabel b
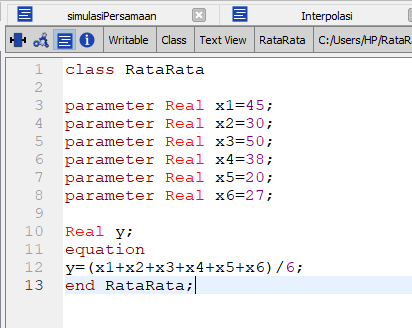
untuk mencari rata-rata pada sejumlah data, maka hanya perlu memasukkan data lalu membuat persamaan mencari rata-rata yaitu Xbar= sigmaX/n(jumlah data).Seperti pada gambar
Tugas 2 : Mencari akar persamaan dengan metode gauss
Seperti yang telah dijelaskan sebelumnya, pak Dai memberi kami tugas untuk menyelesaikan salah satu persamaan linear simultan dengan open modelica. saya memilih untuk mengerjakan Metode Gauss Elimination sebagai objek percobaan saya didalam penyelesaian modelica. pertama-tama saya mencari soal tentang 3 persamaan linear 3 variable yang nantinya akan diubah menjadi matriks 3x3 dengan persamaan A*B=C. dimana matriks A[3x3], B[3], dan C[3]. soulusi yang dicari adalah pada nilai B1,B2, dan B3.
Persamaan sebagai berikut :
Setelah itu, persamaan2 tersebut dibuat dalam bentuk matriks sebelum diselesaikan menggunakan gauss, seperti pada gambar :
sesuai dengan perintah pak dai, kita dianjurkan membuat 2 kelas dalam modelica. yang pertama adalah kelas function dimana kita memasukan fungsi algoritma nya.Kelas yang kedua adalah class dimana nanti function tadi di recall dan dimasukan variable nya lalu solve dilakukan.
Function Matriks
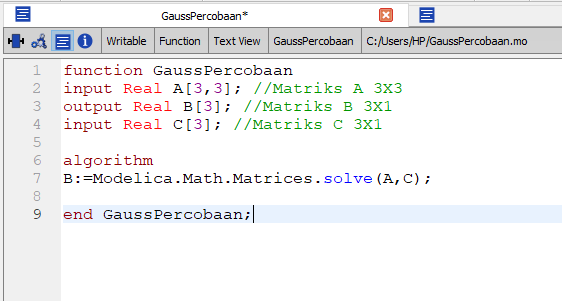
function class diisi dengan mendeclare nilai input,outputdan logartima dimana
input : A[3,3] dan C[3]
output : B[3]
Algoritma : B:=Modelica.Math.Matrices.solve(A,C)
algoritma menggunakan fungsi yang sudah ada didalam modelica yaitu fungsi matrices untuk gauss elimination.
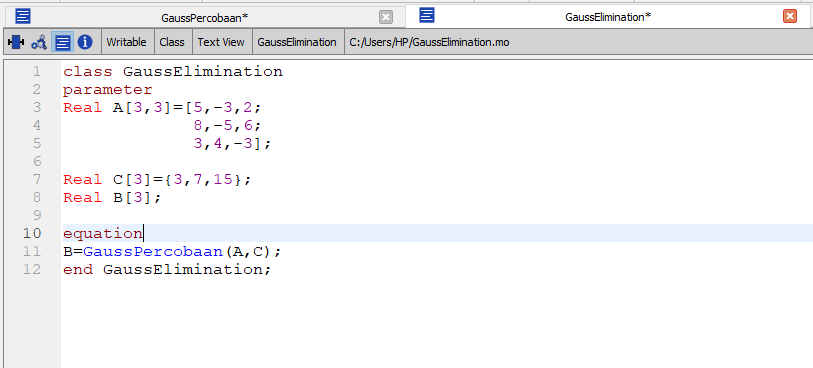
Class Gauss Elimination
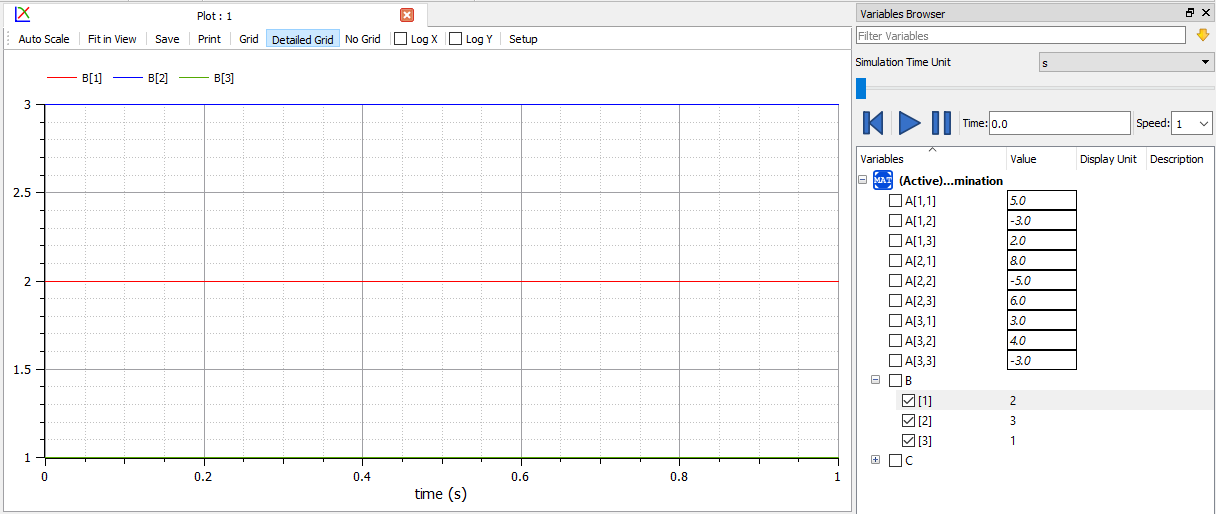
dalam kelas ini, fungsi tadi yang bernama "GaussPercobaan" direcall pada kolom equation dengan memasukan A&C sebagai inputnya dan B outputnya. namun sebelum itu terlebih dahulu saya men-declare nilai2 inputanya tadi seperti digambar atas tersebut
Dari plottingan diatas, diperoleh hasil B1,B2,dan B3 yaitu {2,3,1}
Pertemuan Ketiga, 23 November 2020
Pada pertemuan kali ini, Pak Dai meminta mahasiswa untuk menjawab masalah sehari-hari dengan matriks gauss elimination menggunakan openmodelica.salah satu nya adalah terkait springmass untuk membuktikan hukum Hooke. Berikut adalah soal yang diminta
Function Class
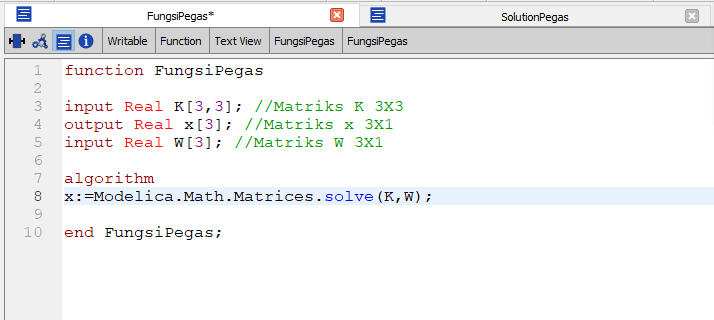
Untuk membuktikan solution di buku tersebut kita menggunakan metode eliminasi gauss sama seperti tugas 2. Pada step pertama, dibuat function class yang bertujuan untuk menginput matriks yang akan dipakai untuk menyelesaikan persamaan.
Class Gauss Elimination
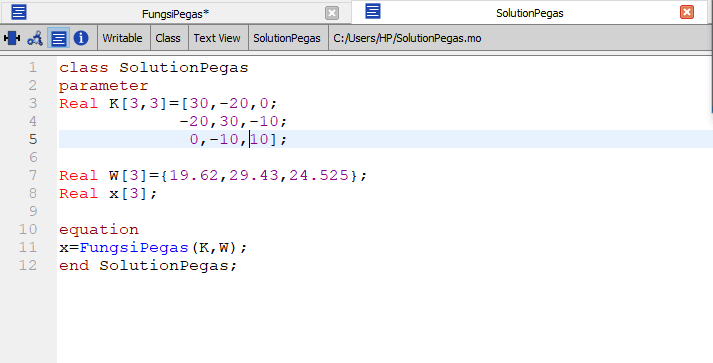
Setelah itu buat class baru yang akan kita gunakan untuk menginput data yang telah diketahui yaitu K dari pegas serta W(berat) dari massa.Selain itu kita melakukan recall pada matriks yang ada pada function class .
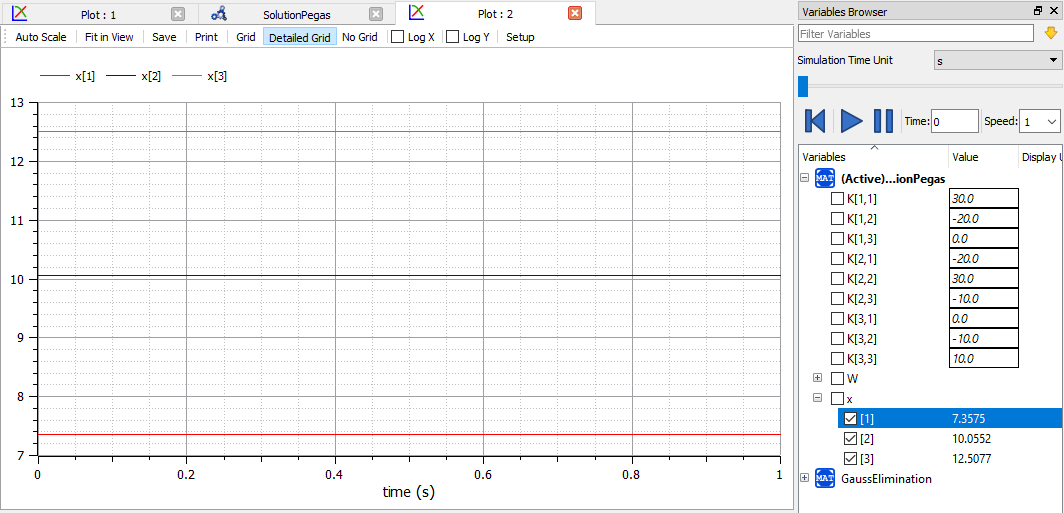
setelah berhasil untuk check model maka jalankan (Simulate) model tersebut. Maka akan didapat plotting sebagai berikut:
Diperoleh x1,x2,dan x3 yang sama dengan yang tertera dibuku
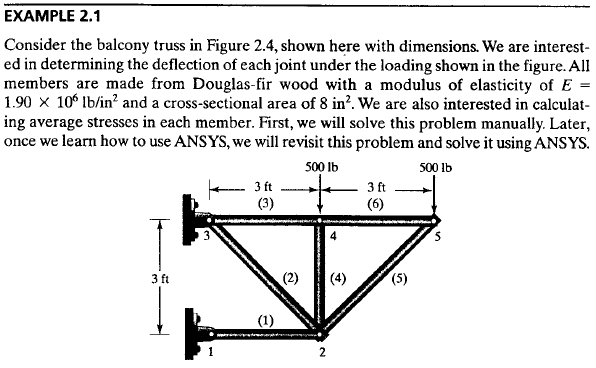
Tugas 3: Menganalisis stress menggunakan openmodelica dengan segmentasi node
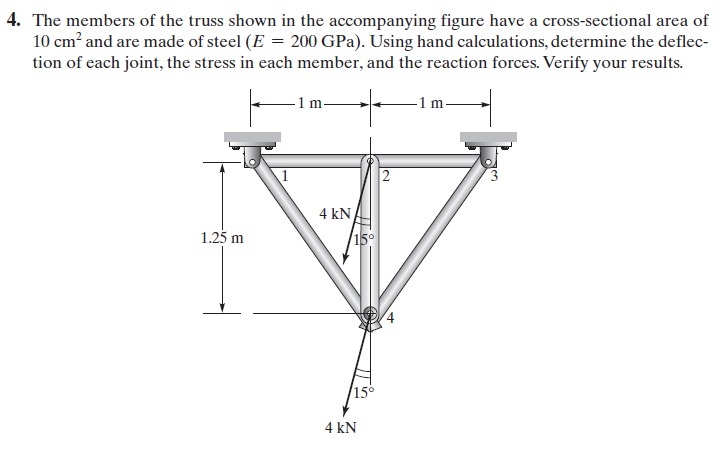
Berikut adalah soal yang diberikan oleh Bapak Dai untuk diselesaikan:
Penyelesaian:
1.Menghitung nilai k dari batang pada setiap elemen
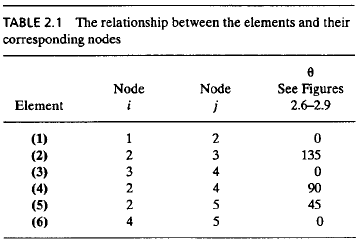
2. Membuat persamaan matriks local untuk kekakuan batang
Elemen 1,3,6 dengan θ:0°
Elemen 4 dengan θ:90°
Elemen 2,5 dengan θ:+-45°
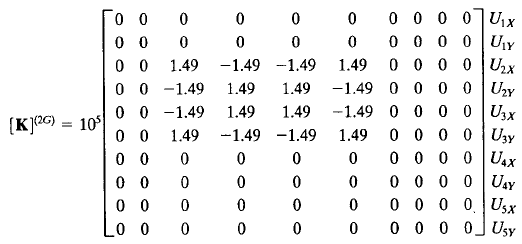
3. Menggabungkan persamaan matriks local menjadi matriks global
4. Memasukkan boundary condition dan membuat persamaan matriks dari hukum Hooke
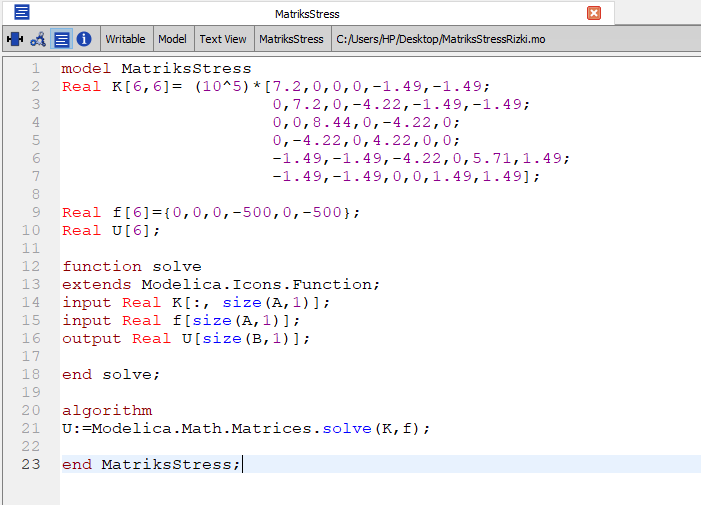
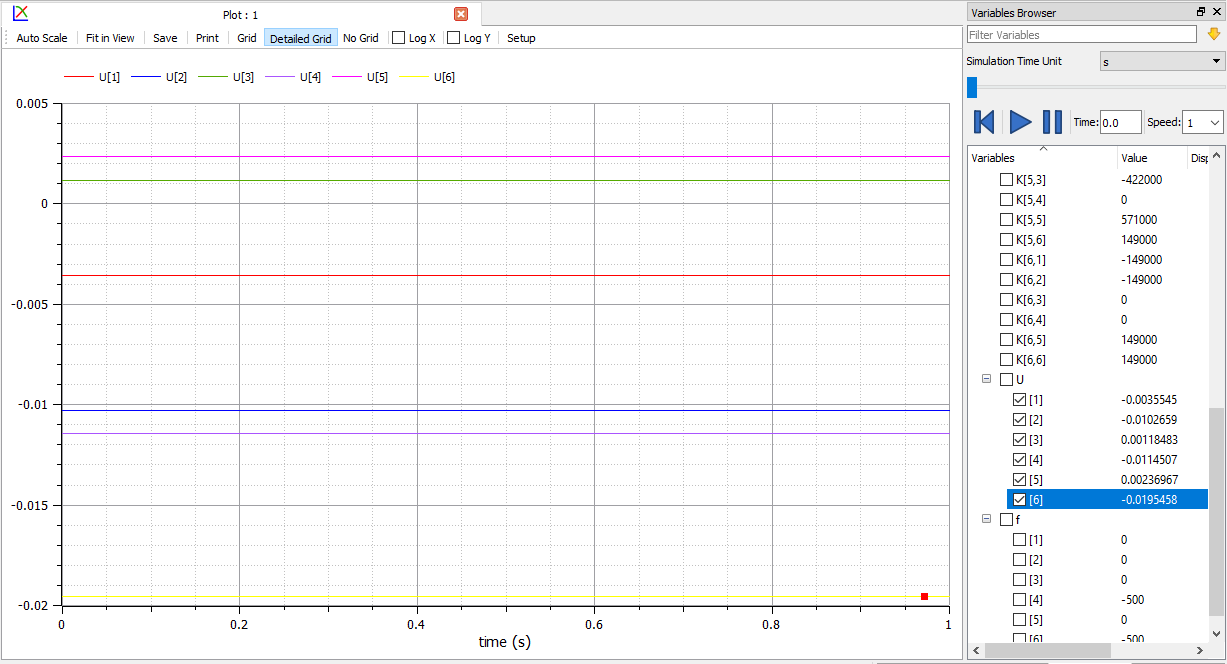
5.Selesaikan dengan openmodelica untuk mendapatkan besar gaya pada elemen batang
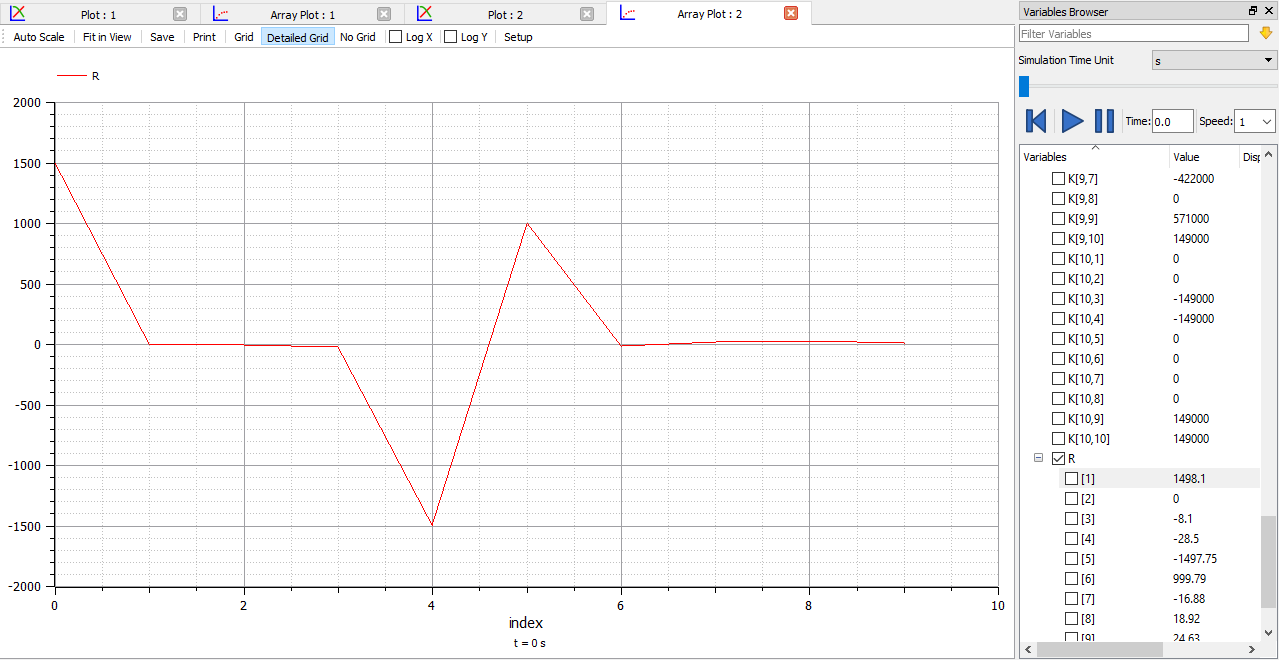
6.Mendapatkan nilai gaya reaksi
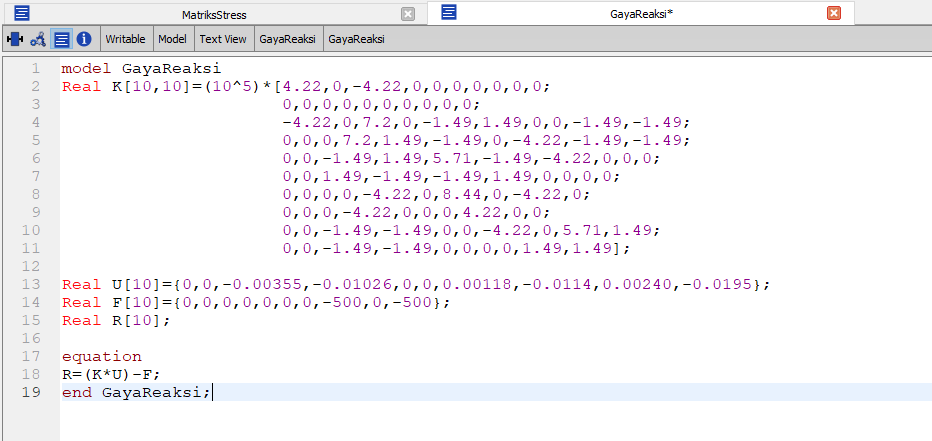
Karena di soal ingin mencari gaya reaksi, maka perlu dilakukan perhitungan pada gaya reaksi dengan persamaan
{R} = [K] {U} - {F}
setelah itu selesaikan dengan openmodelica
File openmodelica dengan format .mo bisa diakses pada drive dibawah
https://drive.google.com/drive/folders/1d8nI9DexidiYvQPuV_s2KMwQGWeoid0p
Pertemuan 4
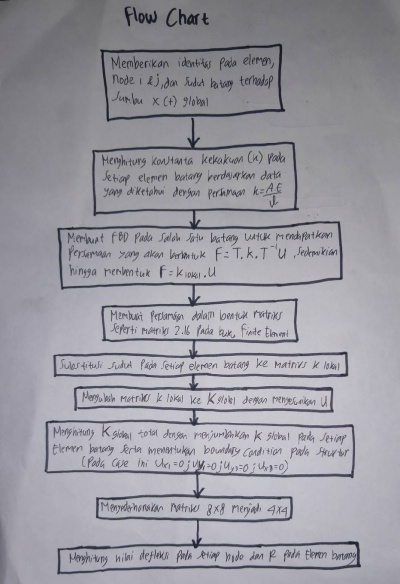
Quiz 1 : Flowchart mencari defleksi dengan analisis elemen
Soal :
Flowchart :
Pertemuan 5
Di pertemuan kali ini, kami membahas tentang soal quiz yang telah diberikan pada pertemuan pekan sebelumnya. sebelum kita mempelajari codingan untuk menyelesaikan soal, kita harus terlebih dahulu mempelajari soal/ masalah yang diberikan.Selanjutnya, dapat lebih memahami pengaplikasian dari software openmodelica pada contoh kasus yang real. Pertemuan ini menjelaskan bagaimana alur pengerjaan soal quiz yang diberikan agar dapat membuat semua persamaan yang dapat digunakan pada kasus yang lebih universal.
Pada pertemuan ini juga, teman saya fahmi menjelaskan mengenai codingan yang telah ia buat. Penjelasannya meliputi :
1.Menjelaskan secara garis besar alur berfikir dari coding itu sendiri.
2.Menjelaskan fungsi if untuk mengubah variabel.
3.Menjelaskan looping menggunakan fungsi for.
4.Menjelaskan apa itu floating number dan kegunaannya dalam matriks.
5.Menjelaskan apa itu protected variable.
Tugas
Setelah pertemuan, pak dai memberikan tugas untuk menganalisis keefektifan codingan yang telah dibuat oleh saudara fahmi.
1. Mempelajari codingan 3d fahmi
Pada codingan fahmi untuk batang 3D, tidak banyak terdapat perubahan pada jumlah function dan class dalam openmodelica, namun terldapat perbedaan pada matriks Inisiasi dimana terdapat dimensi yang baru yaitu nilai cos θx, cos θy, dan cos θz. nilai ini nantinya diperlukan dalam proses pencarian Stiffness dari batang itu sendiri. Selain itu pada codingan 3D, Ukuran matriks K Global menjadi lebih besar yaitu sebesar n*3 dimana n adalah jumlah node
Pada function Stiffness Matriks global, pengonversian K elemen ke K Global, terdapat penambahan pola yaitu 3*n, 3*n-1 ,3*n-2 dimana n akan berubah nodenya sesuai dengan kuadran matriks pada matriks K elemen
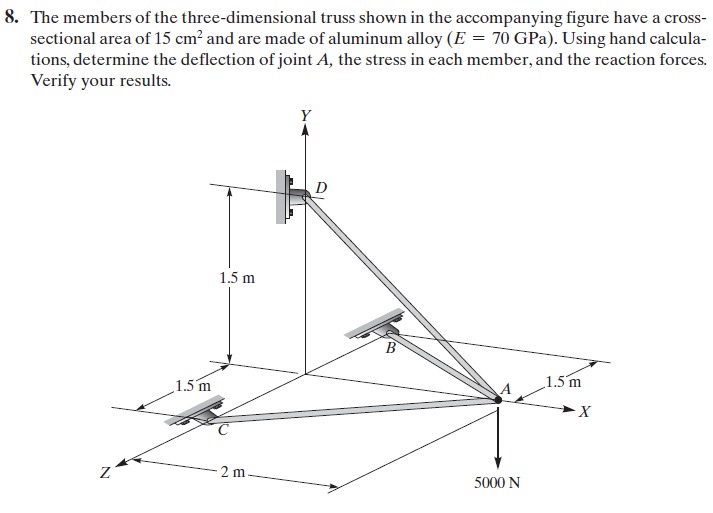
2. Mengaplikasikan pada soal example 3.3
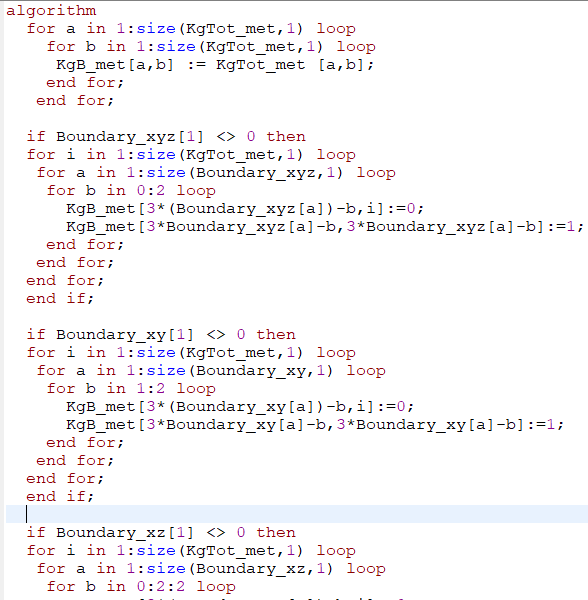
Untuk soal example 3.3, terdapat perbedaan pada kondisi batas setiap node, terdapat node yang memiliki berbagai kondisi batas pada x,y,dan z . Maka diperlukan pendekatan input yang lain yaitu berupa boundary pada xyz ,xy, xz, yz ,x,y,serta z . serta boundary pada class function menjadi sebagai berikut :
Pada function untuk BoundaryStiffnessGlobal juga diperlukan untuk melakukan looping pada setiap boundary xyz ,xy, xz, yz ,x,y,serta z.
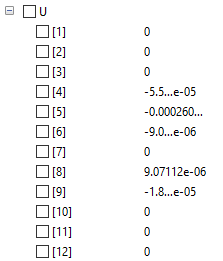
Setelah perubahan tdi dimasukkan, maka dijalankan maka hasilnya sebagai berikut :
3. memberikan masukan atas codingan fahmi
- Pada codingan saudara fahmi, untuk menginput kondisi batas masih hanya untuk kondisi batas Fix dimana tidak ada gaya pada sumbu x dan y . Akan lebih universal lagi jika kemudian kita bisa memasukan kondisi batas untuk berbagai macam jenis tumpuan lain seperti roll dan engsel.
- Pada codingan 3d tersebut juga masih menginput nilai cos θx, cos θy, dan cos θz secara manual untuk matriks inisiasi. Untuk kedepan mungkin lebih bisa agar perhitungan dilakukan melalui codingan yaitu dengan mengurangkan panjang node i dan node j pada setiap batang.
Pertemuan 6: Aplikasi Metode Numerik dalam kasus Optimasi
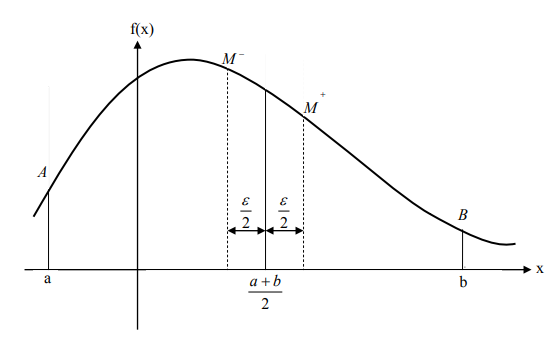
Pertemuan kali ini membahas mengenai optimasi yaitu mencari titik maskimum lokal dan global dari suatu grafik tertentu dimana terdapat fungsi objektif dan constrain tertentu dari grafik tersebut. Dengan metode golden ratio bracket method kita dapat mendapatkan nilai maksimum dari sebuah grafik untuk di analisa titik optimumnya.
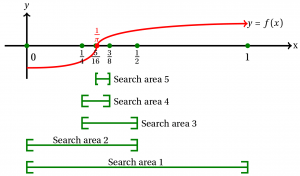
Sesuai dengan namanya, metode ini adalah metode bracket dari interval tertentu serta dicari interval yang benar(Terdapat titik maksimum/minimum) setelah itu melakukannya lagi sebanyak iterasi tertentu
Besar interval yang kita ambil dapat dicari dengan rumus sebagai berikut :
dengan menjalankan iterasi menggunakan open modelica, maka akan diperoleh titik maksimum global/lokal untuk sebuah grafik. Titik tersebutlah yang akan kita jadikan acuan untuk melakukan optimasi pada sebuah sistem/proses.
Pertemuan 7: Review progress tugas besar Optimasi trusses 3D
Dari pertemuan kali ini, dibahas codingan dari josiah,ahmad dan cristo. Pada pertemuan kali ini dijelaskan secara sistematis bagaimana langkah-langkah dalam mencari stress dari trusses serta melakukan optimasi dari data harga material, stress dan luas area dari trusses itu sendiri. Sementara itu, untuk selanjutnya akan di adakan asistensi agar mahasiswa bisa bertanya dan dapat memahami lebih detail terkait codingan yang telah dibuat tersebut.
Tugas Besar Metode Numerik: Optimasi Trusses 3D
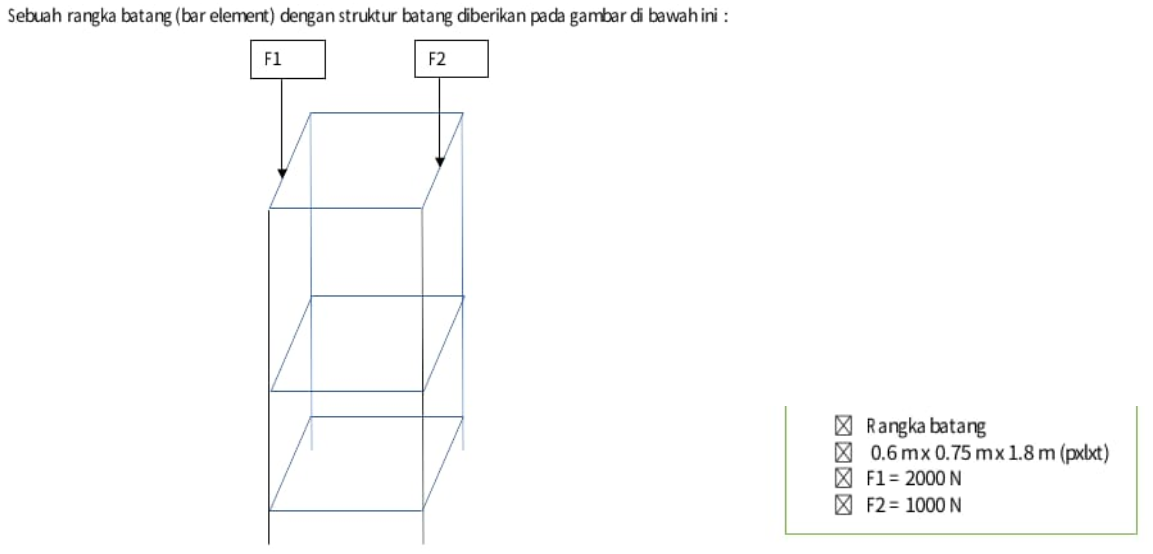
Pada akhir pembelajaran Metode Numerik menggunakan OpenModelica, kami ditugaskan untuk merancang tugas besar yaitu aplikasi Openmodelica dalam kasus optimasi trusses 3D. Secara garis besar, kasus trusses yang sudah ditentukan dilakukan pemodelan melalui coding modelica, setelah itu mulai lah proses optimasi menggunakan program modelica pula. Untuk kasus yang digunakan, ditentukan oleh Pak Dai secara langsung. berikut gambar kasus desain rangka sederhana yang akan dioptimasi:
Dari soal tersebut kita bisa mendefinisikan apa saja yang diketahui pada soal. Pada soal dapat dilihat sebuah rangka berbentuk tray dengan 4 lantai. Dalam rangka tersebut lalu diaplikasikan beban sebesar 1000 N dan 2000 N pada sisi yang berbeda. Dimensi yang dianjurkan adalah Panjang = 0.6 m, Lebar = 0.75 m, dan tinggi = 1.8 m. Beban diaplikasikan pada lebar rangka dengan panjang 0.75m. Tugas kita adalah mengoptimasikan desain tersebut dengan mempertimbangkan sisi efisiensi ekonomi dengan tetap mempertimbangkan kekuatan sistem trusses tersebut.
Adapun Pada gaya 1000N dan 2000N, diasumsikan bahwa gaya terdistribusi merata sebesar 1:1 diantara dua node pada trusses tersebut. artinya pada trusses yang memiliki beban 1000N akan terbagi menjadi 500N di node 1 dan 500N di node 2 begitu juga pada node3 dan 4.
Selanjutnya setelah dicari stress dari trusses tersebut, dilakukan optimasi dengan metode curve-fitting untuk melihat nilai optimum sebuah fungsi objektif. Pada tugas besar kali ini, akan dibuat terlebih dahulu grafik antara Harga material vs stress pada trusses. Akan akan 2 grafik yaitu untuk material konstan namun area berbeda dan material berbeda namun are konstan. Dari kedua grafik tersebutlah kemudian dilakukan optimasi untuk mendapatkan keadaan yang optimum.Asumsi lainnya adalah Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
Langkah-Langkah Pada OpenModelica :
//define initial variable
parameter Integer Points=16; //Number of Points parameter Integer Trusses=24; //Number of Trusses parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) parameter Real Elas=193e9; //Elasticity SS 304 Setelah Komponen dasar pemodelan dideklarasikan, dilakukan pendefinisian connection & koordinat trusses.
Untuk define connection, dibuat kumpulan matriks 1x2 yang berisi 2 nama truss yang dihubungkan. untuk mempermudah pemahaman, susunan koneksi rangka dibangun berdasarkan tingkatan rangka pada desain, seperti lantai 1, 2 , 3 dll. koneksi-koneksi yang ada akan bervariasi sesuai dengan desain dari rangka nya.
Berikut contoh pemodelan Connection yang ada pada program:
model Trusses_3D_Tugas_Besar_Safety
//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=215e6; //Yield Strength (Pa) parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star;
end for;
//Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j]; q2[j]:=P[C[i,2],j]; dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop
if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;