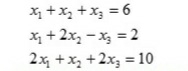Metnum03-Muhammad Aditya Atmadja
Contents
Biodata Diri
Nama : Muhammad Aditya Atmadja
NPM : 1806181786
Kelas : Metode Numerik 03
Pertemuan Pertama
Pada pertemuan pertama, Kami diarahkan untuk mengingat kembali pelajaran sebelum UTS
Materi UTS yang telah kami dapatkan sebagai berikut:
1. Turunan Numerik
Turunan numerik terbagi 3 yaitu:
Turunan Maju (Forward)
Turunan Mundur (Backward)
Turunan Pusat (Centered)
2. Pencarian Akar - Akar Persamaan
Untuk mencari akar - akar persamaan dapat digunakan 2 cara cara yaitu:
Close method (Bracketing) : Terdiri dari graphical method, false position dan bisection
Open method : Terdiri dari newton raphson, secant, dan simple fix point
Interpolasi dan Regresi
Interpolasi adalah metode menghasilkan titik-titik data baru dalam suatu jangkauan dari suatu set diskret data-data yang diketahui.
Regresi adalah salah satu metode untuk menentukan hubungan sebab-akibat antara variabel dengan variabel lainnya.
Selain kita mengingat tentang materi sebelum UTS, Pak DAI menginstruksikan untuk setiap mahasiswa mempelajari OpenModelica. Tutorial yang saya ikuti adalah simulasi feedback yang menggunakan sistem PID melalui video dengan link: https://www.youtube.com/watch?v=Dw66ODbMS2A
Pertemuan Kedua
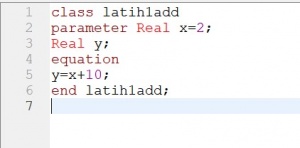
Pada pertemuan ini tiap mahasiswa yang telah mempelajari OpenModelica untuk menunjukkannya pada zoom call. Setelah selesai, Pak Dai mengajarkan bagaimana cara melakukan perhitungan dengan menggunakan openmodelica. kami membuat program sederhana dalam modelica untuk menjumlahkan angka 10 kepada sebuah variabel. Berikut hasilnya:
Lalu kami diberi tugas untuk melakukan perhitungan rata-rata.
Lalu didapatkan hasil rata-rata sebagai berikut:
Tugas
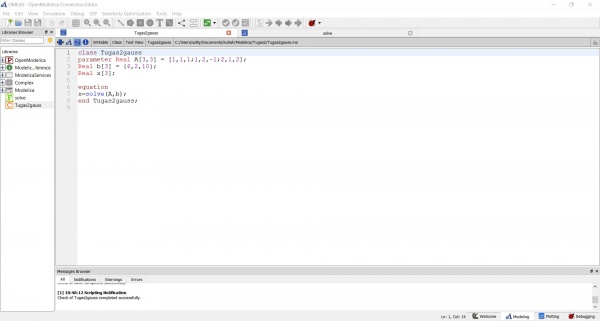
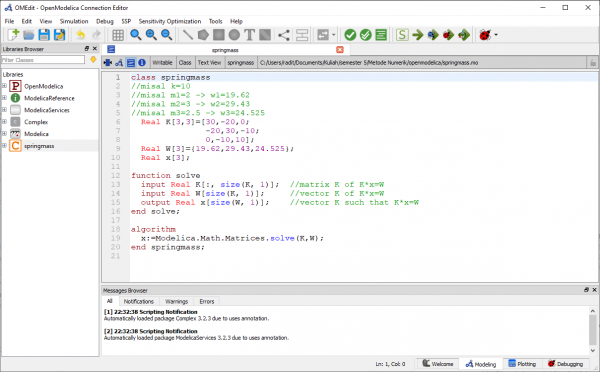
Pada tugas ini saya menyelesaikan persamaan berikut
Pada penyelesaian persamaan tersebut saya menggunakan metode eliminasi gauss
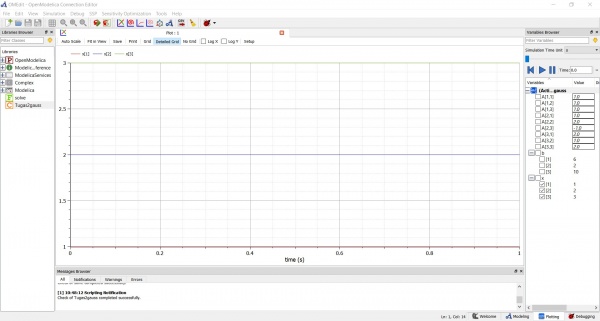
Dari perhitungan diatas didapatkan nilai x1=1 , x2=2 , dan x3=3
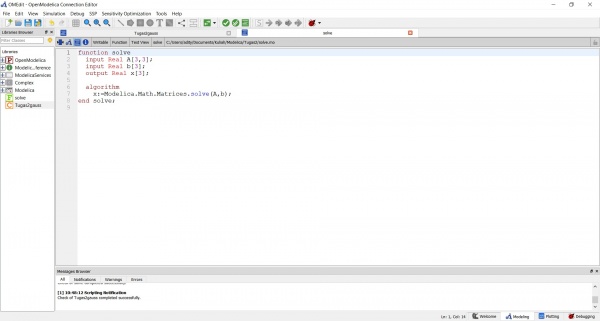
Referensi yang saya gunakan pada penyelesaian diatas menggunakan link https://build.openmodelica.org/Documentation/Modelica.Math.Matrices.solve.html
Pertemuan 3
Pada pertemuan ini, kami diminta untuk menjelaskan tugas aljabar simultan, selanjutnya kami diminta untuk mencoba mengerjakan soal
Kode yang digunakan adalah sebagai berikut
Tugas 3
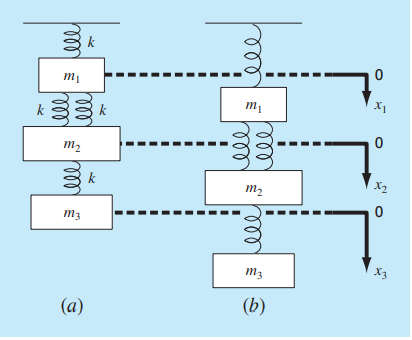
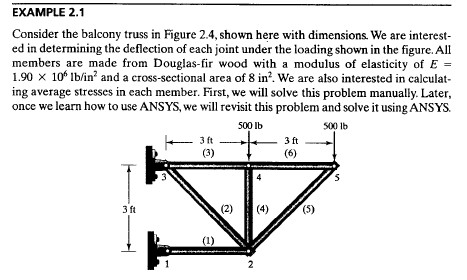
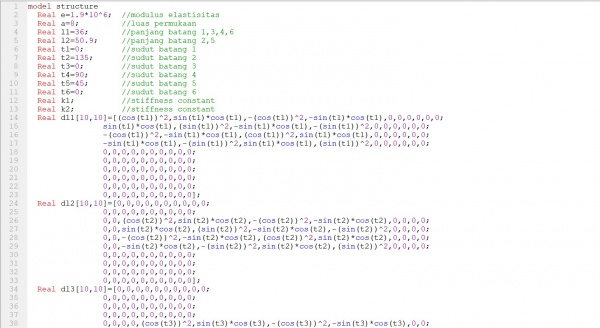
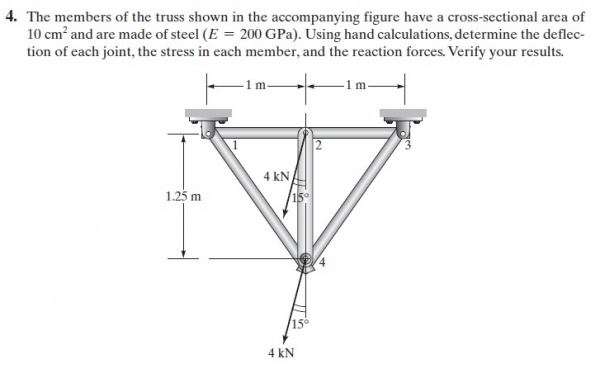
Tugas ini kami menghitung defleksi pada setiap batang dan gaya reaksinya.
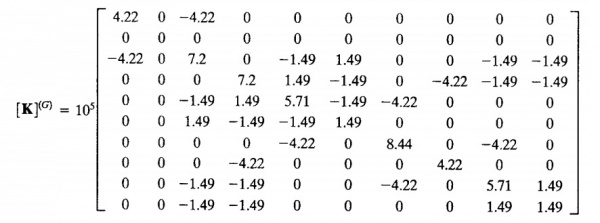
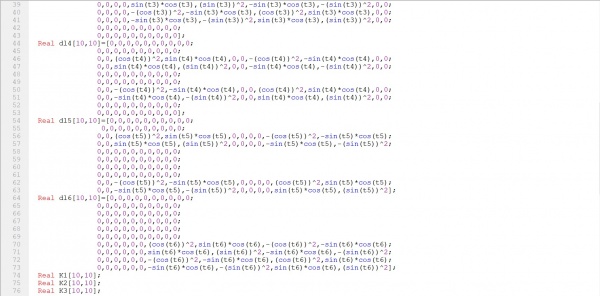
matriks lokal digabung sehingga mendapatkan matriks global
Saya cari matriks posisi global untuk seluruh node dengan coding berikut:
Hasil koding
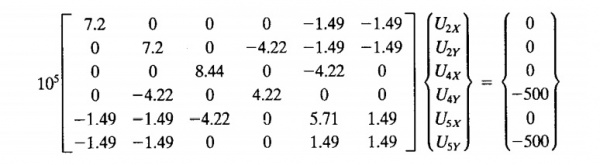
Kemudian masukkan boundary conditionnya. Pada node 1 dan 3 fix, sehingga U1x,U1y,U3x,U3y=0. Pada node 4 dan 5 diberikan gaya eksternal dengan F4y = -500lb dan F5y = -500lb. Boundary condition tersebut kemudian dimasukkan dalam persamaan {F}=[K]g*[U].
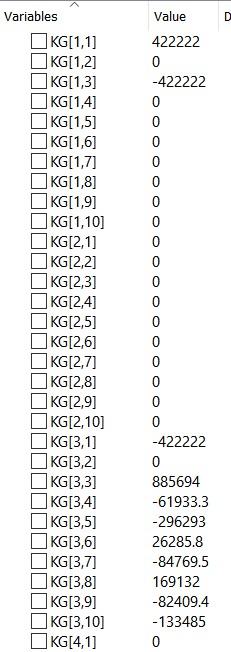
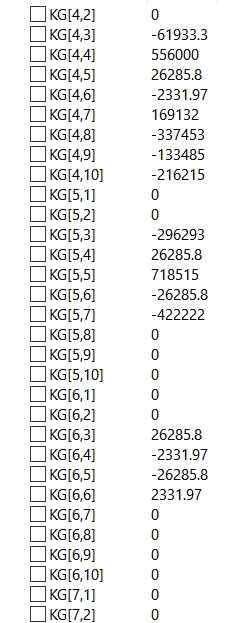
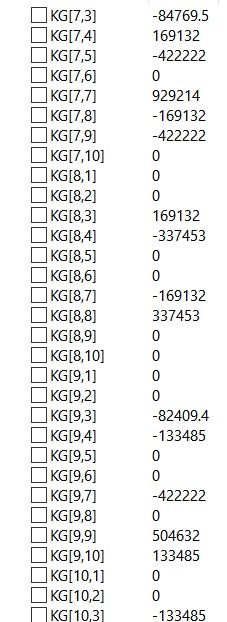
Dengan menggunakan eliminasi gauss didapatkan matriks global
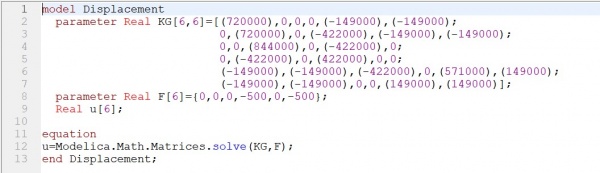
Untuk mencari nilai U atau displacement, saya menggunakan coding sebagai berikut:
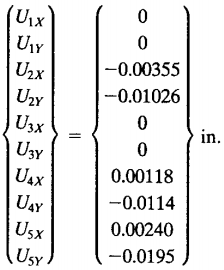
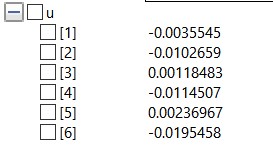
Hasilnya adalah
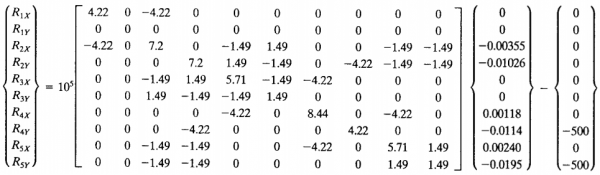
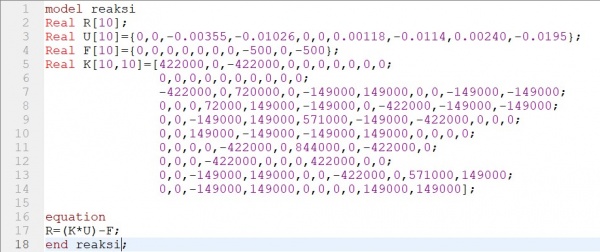
menentukan gaya reaksi dengan rumus {R}=[K]g{U}-{F}
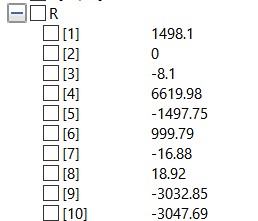
untuk mencari gaya reaksi saya gunakan kode berikut
hasilnya adalah
File yang digunakan dapat diunduh dengan link berikut
https://drive.google.com/drive/folders/1PvrxD9vmdkvBj99Qqs0fi7nWCkrWlE6y?usp=sharing
Pertemuan 4
Pada pertemuan ini kita mengawali dengan membahas tentang perbedaan statika struktur dan dinamika struktur. Dapat disimpulkan dengan singkat statika struktur berbeda dengan dinamika struktur, pada statika struktur beban seperti contohnya di trusses tetap sedangkan pada dinamika struktur bebannya bisa berubah sewaktu-waktu seperti contohnya ada gempa bumi atau faktor eksternal lainnya.
Quiz
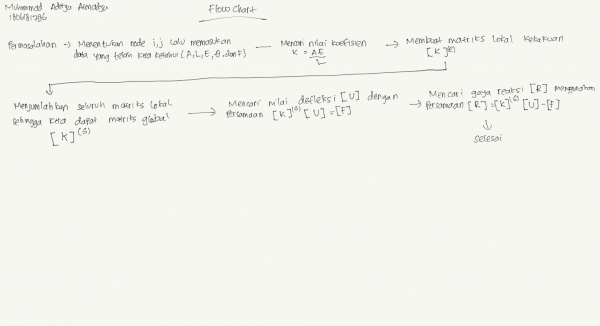
Soal yang diberikan adalah sebagai berikut
Lalu saya buat flowchart seperti berikut
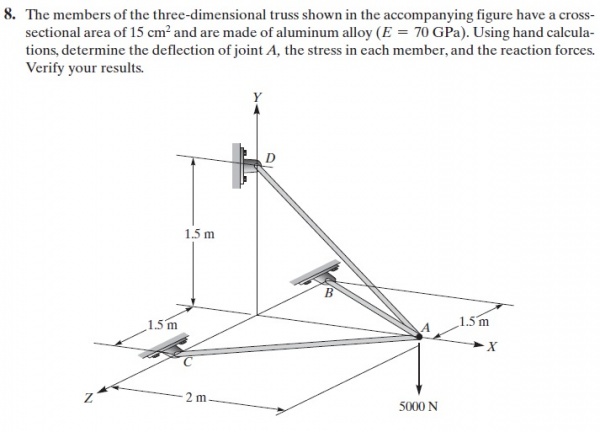
Nomor 4
Class
class no1Quiz
// DECLARATIONS
// Data for each member: [element #, node i, node j, theta, area, modulus, length]
// SI Units: [integer, integer, integer, degrees, meters^2, pascals, meters]
// Imperial Units: [integer, integer, integer, degrees, inches^2, lb/inches, inches]
parameter Real [:,7] member = [1, 1, 2, 0, 8, 1.9e6, 36;
2, 2, 3, 135, 8, 1.9e6, 50.9;
3, 3, 4, 0, 8, 1.9e6, 36;
4, 2, 4, 90, 8, 1.9e6, 36;
5, 2, 5, 45, 8, 1.9e6, 50.9;
6, 4, 5, 0, 8, 1.9e6, 36];
// External loads for each node: [node #, FX, FY]
parameter Real [:,3] node_load = [1, 0, 0;
2, 0, 0;
3, 0, 0;
4, 0, -500;
5, 0, -500];
// Vector for equivalent stiffness constant of each member
Real [size(member,1)] k;
// Array for Stiffness Matrix
Real [size(member,1),4,4] Ke;
equation
// Calculate stiffness constants for each member element
k = {(member[i,5] * member[i,6] / member[i,7]) for i in 1:size(member,1)};
// Find stiffness matrix for each element
Ke = stiffnesselement(member);
end no1Quiz;
Pertemuan 5
Pada pertemuan kali ini, kami membahas kembali tentang PR sebelumnya yaitu nomor 4 dan 8. Teman saya, Ahmad Mohammad Fahmi menjelaskan tentang coding yang dia buat dari awal sampai akhir. Namun, coding dari Fahmi masih ada yang kurang, karena total gaya pada ketiga sumbu untuk soal nomor 8 masih belum sama dengan 0. Selain itu Fahmi menjelaskan kepada teman-teman di kelas tentang fungsi-fungsi yang saya gunakan untuk mengerjakan soal quiz. Beberapa hal yang saya jelaskan antara lain:
1. Cara melakukan looping menggunakan fungsi for.
2. Cara membuat data dalam bentuk array.
3. Cara menggunakan fungsi if.
4. Apa itu floating number dan bagaimana cara menghilangkannya.
5. Apa itu protected variable.
6. Fungsi dari modelica class dengan specialization class dan function.
Tugas Besar
Pada tugas besar ini kita diminta untuk mengoptimasi pemilihan material
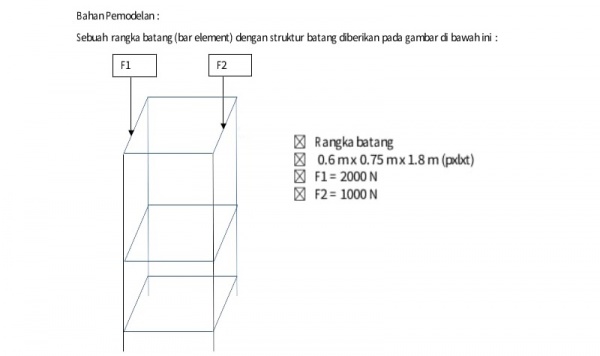
Diketahui:
F1 = 2000 N F2 = 1000 N Dimensi = 0.6 m x 0.75 m x 1.8
Langkah yang dilakukan
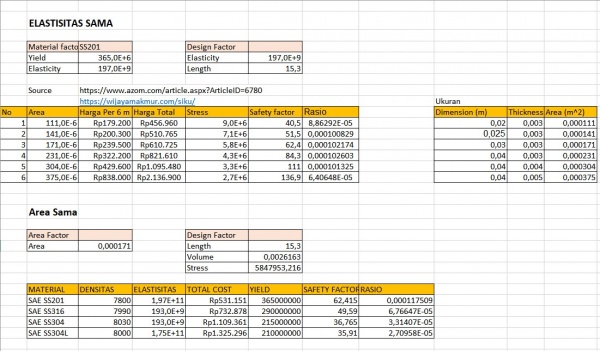
Pada jenis material sama:
1. Cari harga material SS201 untuk 6 ukuran batang yang berbeda 2. Hitung Safety factor 3. Buat rasio dengan membagi safety factor dan total cost 4. Membuat persamaan rasio dengan menggunakan metode curve fitting 5. Melakukan optimasi dengan metode golden section
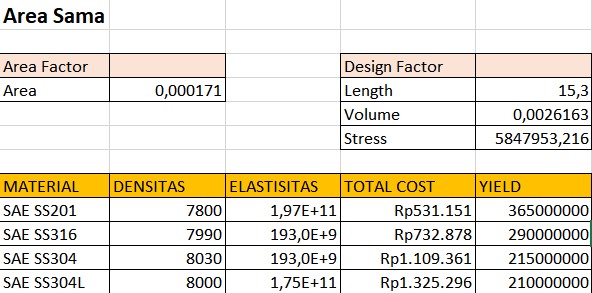
Pada area yang penampang sama:
1. Cari harga 4 material dengan area penampang yang sama 2. Hitung safety factor 3. Buat rasio dengan membagi safety factor dan total cost 4. Membuat persamaan rasio dengan menggunakan metode curve fitting 5. Melakukan optimasi dengan metode golden section
Dengan asumsi sebagai berikut:
Beban akan terdistribusi hanya pada node (karena bersifat trusses). Safety factor minimal bernilai 2. Batas displacement 0,001 m sebelum buckling (pada truss paling atas).
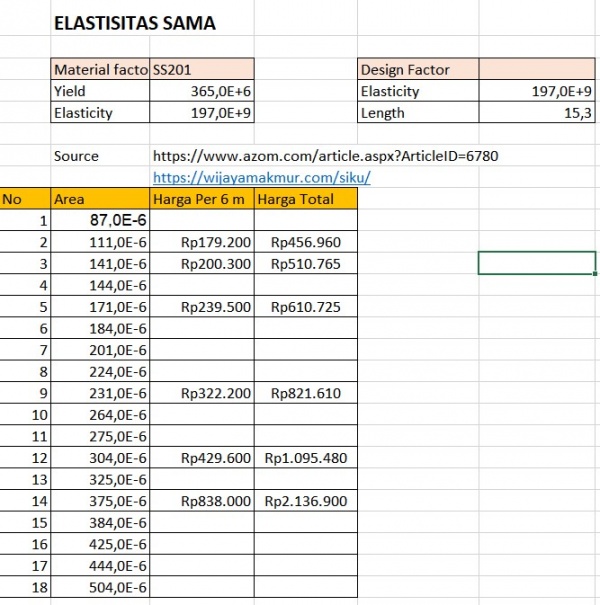
Data yang Digunakan
Coding yang digunakan untuk displacement, reaction force, stress, dan safety factor
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=365e6; //Yield Strength (Pa)
parameter Real Area=0.000171; //Area L Profile (Dimension=0.03, Thickness=0,003) (m2)
parameter Real Elas=197e9; //Elasticity SS 201 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
Hasil perhitungan
-Nilai rasio dan safety factor
Untuk Curve fitting
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); end Curve_Fitting; for i in 1:3 loop for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R); end for;
Untuk golden section
model Opt_Gold
parameter Real xd[:]={111e+6,141e+6,171e+6,231e+6,304e+6,375e+6};
parameter Real yd[size(xd,1)]={8.86e-5,0.000100761,0.000102198,0.000102622,0.000101289,6.405e-5};
parameter Real xlo=86e+6;
parameter Real xhi=500e+6;
parameter Integer N=6; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Hasil Nilai luas area penampang optimum untuk material SS201 adalah 485mm^2