Rezky Alfian Fatra
| Profile | |
|---|---|

| |
| Nama Lengkap | Rezky Alfian Fatra |
| NPM | 1906379043 |
| Jurusan | Teknik Mesin |
Rezky Alfian Fatra (lahir di Jakarta, 13 November 2000; umur 20 tahun) adalah seorang mahasiswa yang mengambil jurusan Teknik Mesin di Universitas Indonesia angkatan 2019. Selain menjalankan tugas utama menjadi seorang mahasiswa, Rezky juga dikenal aktif berkontribusi di Lembaga Dakwah Kampus,khususnya di IMM yang memberikan wawasan berupa ilmu keagamaan kepada mahasiswa Departemen Teknik Mesin.Salah satu hal yang dilakukan oleh Rezky adalah dengan membuat program kerja yang menjadi wadah bagi mahasiswa Departemen Teknik Mesin untuk meningkatkan wawasan maupun kemampuan keagamaanya.
Contents
Aktivitas
Rezky Alfian Fatra atau panggilan akrabnya adalah Ekky adalah seorang mahasiswa yang aktif dalam melakukan kontribusi semenjak SMA, khususnya dalam bidang dakwah agar bisa memberikan manfaat bagi orang banyak.Ini terbukti dengan banyaknya organisasi rohani islam yang pernah ia jalani
Sangat besar harapan saya agar terus bisa berkontribusi memberikan kebaikan yang bisa bermanfaat dan berguna bagi orang banyak, seperti yang pernah disabdakan oleh Nabi Muhammad SAW : "Sebaik-baiknya manusia adalah manusia yang bermanfaat untuk orang lain."
Dalam aktivitasnya menjadi seorang pendakwah yang memberikan manfaat bagi orang banyak, Rezky juga tidak lupa untuk terus menambah ilmunya dengan mengikuti kajian keagamaan yang diselenggarakan oleh Manazil Ilmi Insani (Meninggikan Ilmu Manusia)
Metode Numerik
Metode numerik merupakan sebuah metode yang digunakan untuk menyelesaikan persoalan dimana perhitungan yang dilakukan secara analitik sudah sulit atau bahkan tidak bisa untuk dilakukan.Metode numerik ini berawal dari sebuah pemikiran bahwa permasalahan dapat diselesaikan dengan menggunakan pendekatan-pendekatan yang dapat dipertanggungjawabkan dengan metode analitik.Dengan menggunakan metode numerik, kita bisa mendapatkan hasil yang cepat dan tepat (meskipun dengan menggunakan pendekatan).
Pada kelas Metode Numerik-02 semester ganjil 2020/2021, dari awal perkuliahan sampai UTS diisi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Dimana pada pertemuan yang telah dilakukan telah membahas materi seperti:
- Pseudocode
- Sistem Persamaan
- Turunan Numerik
- Metode Newton Rhapson, Secant, dan Bisection
- Regresi Linear
- Interpolasi
Setelah UTS pembelajaran diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara
Pertemuan Perkuliahan
Pertemuan Pertama (Rabu, 11 November 2020)
Pada pertemuan pertama yang diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara. Mahasiswa dijelaskan mengenai esensi atau tujuan pembelajaran metode numerik, yaitu:
1. Memahami konsep-konsep dan prinsip-prinsip dasar dalam metode numerik seperti:Persamaan algoritma, aljabar, pencocokan kurva, persamaan diferensial parsial, dan lainnya
2. Mengerti dan mampu menerapkan pemahaman atau aplikasi terhadap konsep metode numerik
3. Mampu menerapkan metode numerik dalam hal terkait persoalan keteknikan
4. Mendapat added value (nilai tambah)/adab sehingga mahasiswa menjadi orang yang memiliki budi pekerti yang baik
Selain empat poin yang telah disebutkan, Mahasiswa juga mendapatkan pelajaran terkait penggunaan aplikasi OpenModelica. Dimana Mahasiswa dijelaskan dengan sangat sistematis mengenai penggunaan sederhana OpenModelica.Bahkan Bapak Dr. Ir. Ahmad Indra Siswantara juga menjelaskan bahwa komputer memiliki limit atau batasan yang tidak dapat dilampauinya.Pada misalnya saja komputer tidak mampu menentukan nilai 1/0 yang hanya Tuhan yang tahu nilainya. Pelajaran atau hikmah yang dapat diambil dari kasus ini adalah manusia haruslah beriman dengan Rabb-Nya dan jangan pernah melupakan Tuhan yang mengetahui dan berkuasa atas segala sesuatu.
Tugas minggu pertama
Pertemuan Kedua (Rabu, 18 November 2020)
Pada pertemuan minggu ke-2, beberapa mahasiswa dimintai untuk mempresentasikan hasil tugas yang diberikan pada minggu pertama.Selain itu, pada pertemuan kali ini, Bapak Dr. Ir. Ahmad Indra Siswantara juga mengajari mahasiswa mengenai fitur class dan function.Alasan Bapak Dr. Ir. Ahmad Indra Siswantara memilih untuk menggunakan open modelica, yaitu karena aplikasi ini lebih mudah untuk digunakan (tidak butuh spesifikasi yang tinggi) dan bisa digunakan secara gratis oleh mahasiswa.
Untuk tugas minggu ke dua, mahasiswa diminta untuk mempelajari lagi open modelica dan melakukan sistem panggil class dan function.Berikut tugas saya dengan menggunakan contoh soal Aljabar Linier dengan ordo 4x4
Pertemuan Ketiga (Rabu, 25 November 2020)
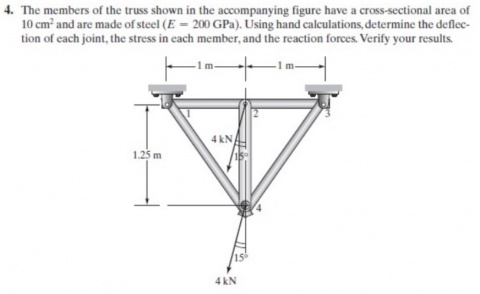
Tugas 3
- Berikut adalah soal untuk tugas kali ini:
- Penyelesaian:
Persamaan
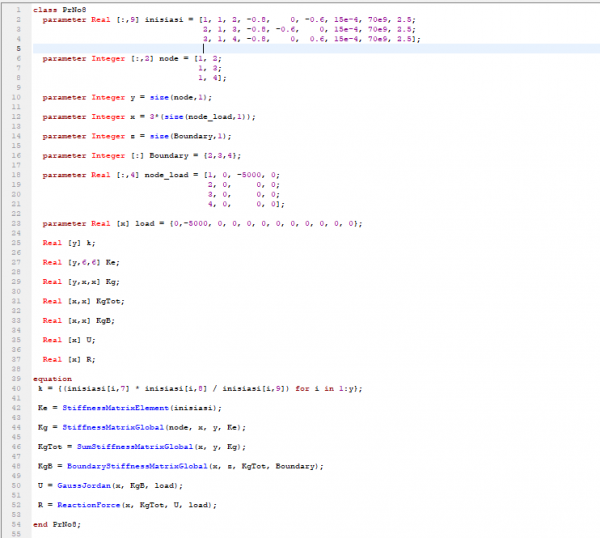
class Trusses_Tugas3_RezkyAlfianFatra
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_Tugas3_RezkyAlfianFatra;
Fungsi Panggil
|
Matrice Transformation function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
|
Global Element Matrice function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
|
Reaction Matrice Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; |
Gauss Jordan
|
function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop if abs(X[i]) <= float_error then X[i] := 0; end if; end for; end Gauss_Jordan; |
Pertemuan Keempat (Rabu, 02 Desember 2020)
Tugas 4
Pr No 8 kami diminta untuk menyelesaikan permasalahan 3D dengan membuat class diagram, flowchart, dan penyelesaiannya dengan openmodelica
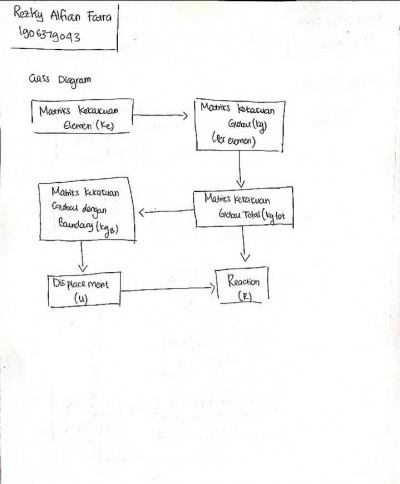
Pertama saya membuat class diagram
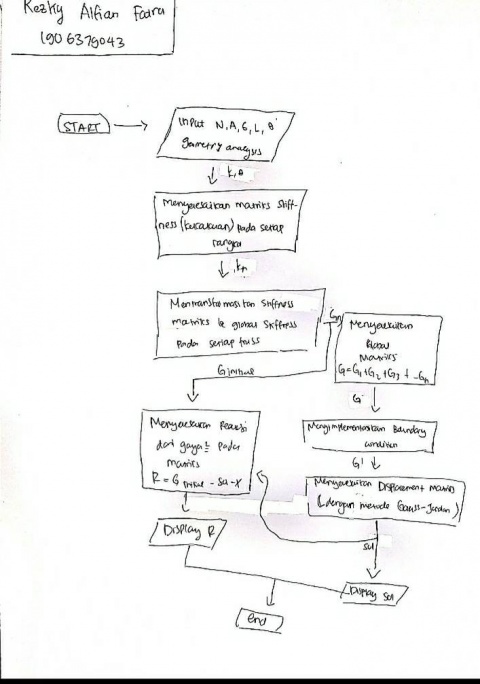
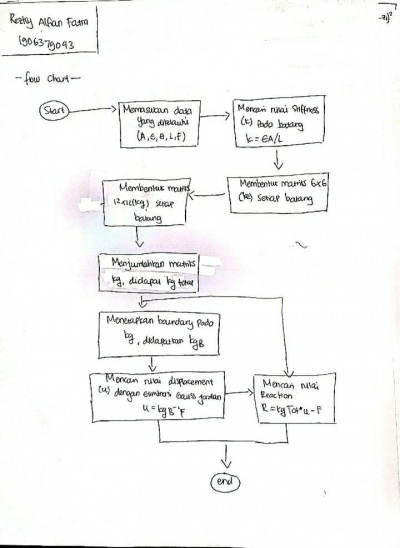
Kemudian saya membuat flowchart
Setelah itu, saya membuat Free Body Diagram (FBD) untuk mencari data-data yang diperlukan pada persoalan ini.Data tersbut berupa node, modulus elastisitas, luas, sudut, dan panjang dari setiap batang.Karena pada kasus ini merupakan permasalahan 3D (3 Dimensi), maka sudut akan berada pada arah X, Y, dan Z.Rumus untuk mencari panjang batang, bisa kita dapatkan di buku.Untuk gaya eksternal yang ada, kita dapat melihatnya dari gambar yang hanya berada di node 1 arah sumbu y.Kemudian setelah itu, data-data yang ada kita ubah menjadi bentuk matriks agar bisa diselesaikan dengan menggunakan openmodelica
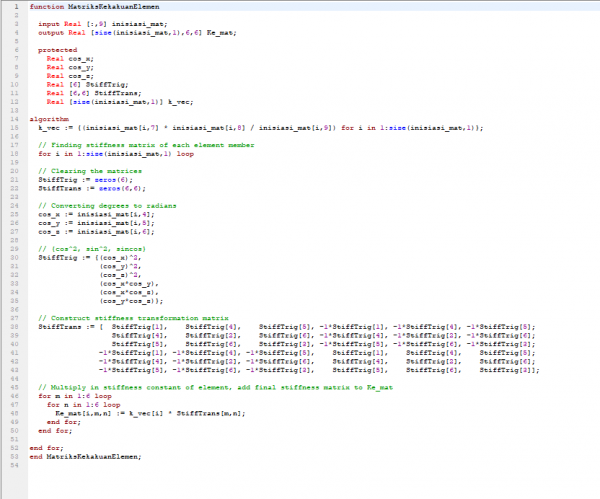
Untuk mendapatkan nilai K dapat menggunakan rumus K=AE/L.Setelah mendapatkan nilai K pada setiap batang, nilai tersebut digunakan untuk membuat matriks K elemental (Ke) pada setiap batang
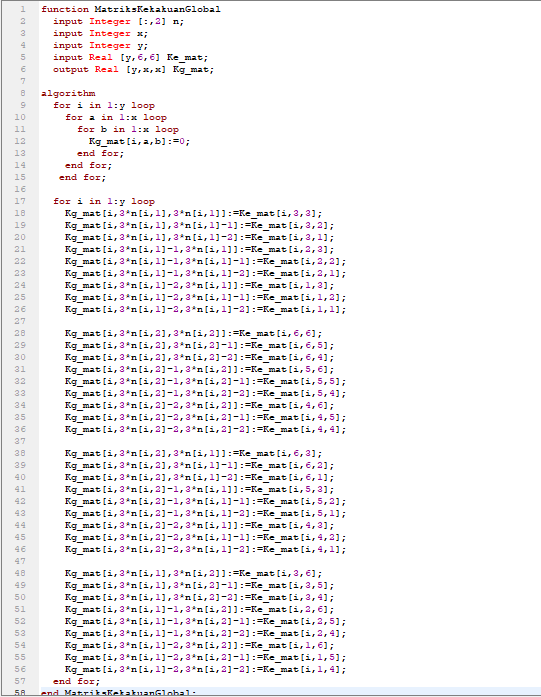
Kemudian matriks 6x6 tersebut akan dibuat menjadi matrks 12x12 sesuai dengan jumlah batang yang ada (3)*jumlah node (4).Ini disebut dengan matriks kekakuan global (Kg)
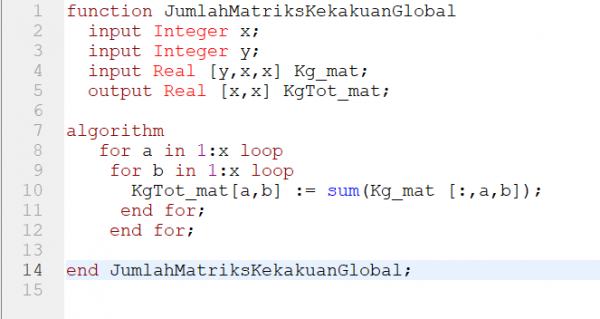
Selanjutnya matriks kekakuan pada setiap batang dijumlahkan agar mendapatkan matriks kekakuan global total
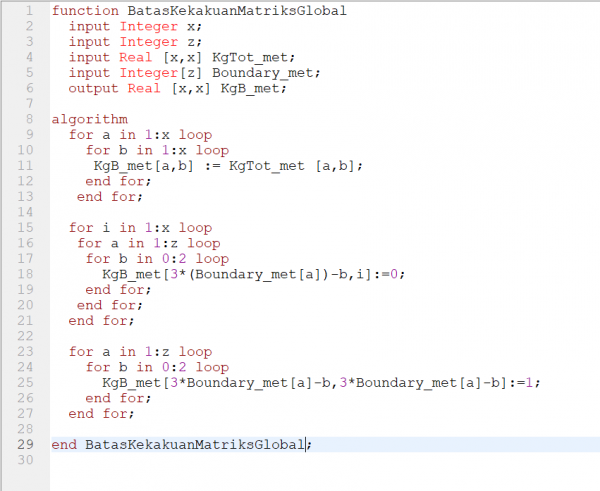
Setelah itu, boundary diterapkan pada matriks kekakuan global total.Pada kasus yang ini, node 2, node 3, dan node 4 merupakan pinned. Sehingga U2X=U2Y=U2Z=U3X=U3Y=U3Z=U4X=U4Y=U4Z=0.
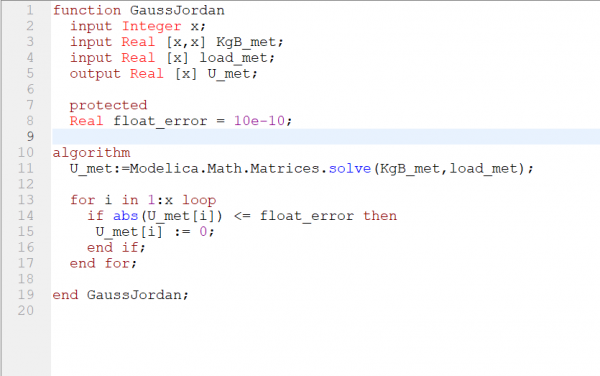
Untuk mencari nilai U atau nilai displacement lainnya menggunakan Eliminasi Gauss Jordan dengan menggunakan persamaan XU=F. Dengan X adalah matriks K global yang sudah menerapkan boundary (KgB) dan F didefinisikan sebagai eksternal load
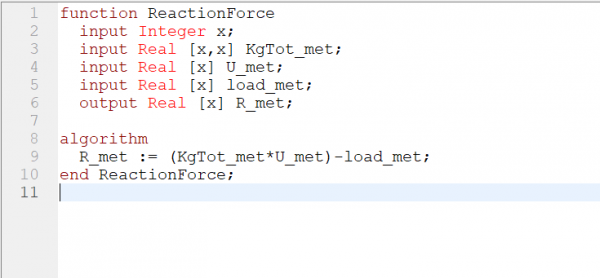
Sedangkan untuk mencari reaction force dapat menggunakan persamaan R=Kg*U-F
Function-function tersebut akan dipanggil ke dalam sebuah class untuk penyelesaiannya. Pada class juga akan diinput data-data yang telah dicari pada langkah pertama
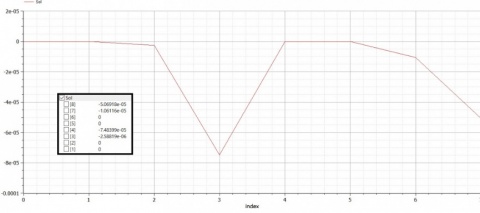
Sehingga, setelah disimulate, kita akan mendapatkan nilai displacement (U)
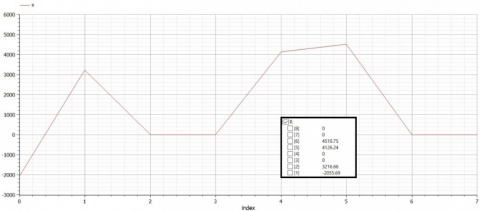
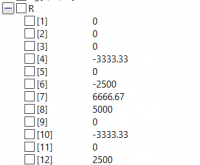
dan Nilai R
Berikut video penjelasannya
Pertemuan Keenam
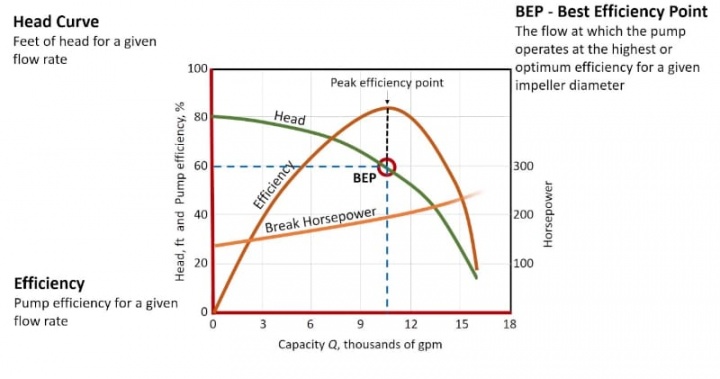
Sistem optimasi dalam sebuah sistem fluida ada yang berupa zat cair seperti aliran darah, dan juga ada yang berupa gas seperti sistem pernapasan.Yang ditampilkan pada grafik dibawah ini adalah sebuah karakteristik dari sistem dan komponen. sistem fluida tidak hanya perpipaan, tapi juga mesin kerja berupa pompa dan tenaga, ada valve, dan juga ada pipa belok.Sistem fluida, aliran air dimasukan dari yang tediri pompa, pipa, pipa belok (T,L) valve.Pada setiap komponen memiliki tujuan yang sama, yaitu mengalirkan air dari sebuah tempat ke tempat yang kita tuju.Sistem tersebut adalah pompa, dengan menggunakan sistem pendukung, memberikan tenaga pada pompa
-Yang melengkung pada grafik tersebut adalah efisiensi -Break housepower -Sumbu datar adalah jumlah aliran yang diantarkan -Sumbu y adalah efisiensi dari pompa -Garis hijau merupakan tenaga air yang keluar dari pompa -Pada saat jumlah air yang dikeluarkan tekanan akan turun dan breakhouse power akan naik -Pada efisiensi, makin tinggi kapasitasnya maka efisiensinya akan naik. Terdapat juga titik maksimum dan kemudan setelah itu efisiensi akan menurun -Untuk efisiensi pada sistem, mempertimbangkan heatloss pada kondisi tertentu
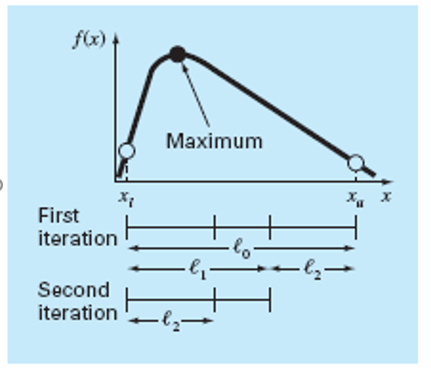
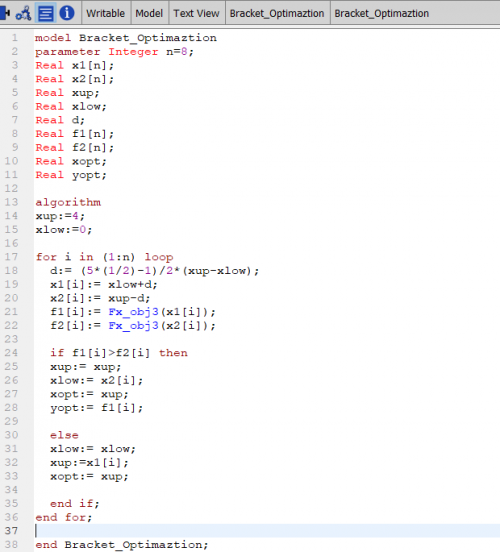
Pembahasan berikutnya mengenai metode Bracket Optimization Using Golden Ratio Method yang dijelaskan oleh bu Chandra.Jika ingin menyelesaikan suatu permasalahan dengan menggunakan cara optimasi, kita harus paham terlebih dahulu mengenai materinya
- Menentukan dan mengetahui batasan titik awal terendah (xL) dan tertinggi (xH)
- Mendapatkan nilai x1 dan x2 dari golden ratio (d)
- Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru
- Mendapatkan nilai x1 dan x2 baru
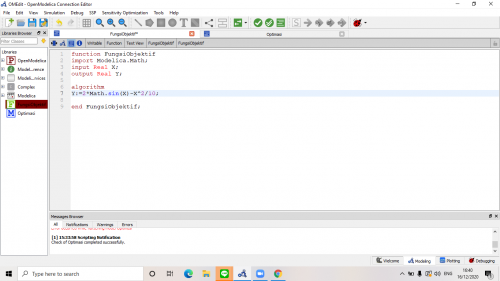
Jika dalam soal diketahui untuk menyelesaikan persamaan y=2sinx-x^2/10,kemudian fungsi ini dimasukkan ke dalam openmodelica, kemudian fungsi tersebut akan dipanggil
Setelah di cek dan tidak terjadi masalah dalam simulate openmodelica, dapat dibuat model yang akan memanggil fungsi tersebut
Progress Tugas Besar
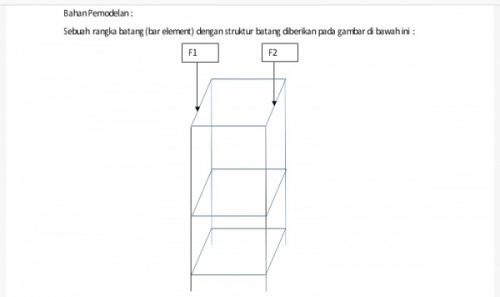
Tugas besar yang diberikan kemarin untuk kelas metnum 02 dan 03 adalah menghitung dengan menggunnakan optimasi untuk rangka batang:
suatu rangka batang yang telah dibentuk seperti gambar diatas, dengan spesifikasi sebagai berikut:
Diharapkan dari persoalan di atas dapat mendesain rangka batang dengan harga yang terjangkau dan optimal.
Faktor atau variabel bebasnya meliputi : Harga, Material yang digunakan, dan cross section