Akmal Rayhansyah
Perkenalan Singkat
Nama : Akmal Rayhansyah H. N.
NPM : 1906356361
TTL : Bandung, 28 November 2000
Halo, perkenalkan saya Akmal Rayhansyah. Teman-temanku biasa memanggil saya Akmal. Saya adalah seorang mahasiswa Teknik Mesin Universitas Indonesia angkatan 2019. Saya memilih jurusan teknik mesin karena saya memiliki ketertarikan di bidang permesinan terutama pada bidang manufaktur otomotif. Saat ini saya sedang berpartisipasi di tim Universitas Indonesia Super Milage Vehicle sebagai staf. Alasan mengapa saya berpartisipasi dalam tim tersebut adalah agar saya dapat gambaran mengenai ketertarikan saya dalam manufaktur otomotif tersebut.
Metode Numerik
Metode numerik itu sendiri merupakan suatu teknik penyelesaian permasalahan yang diformulasikan secara matematis dengan menggunakan operasi aritmatika. Metode ini digunakan disaat ada sebuah permasalahan matematis yang tidak bisa diselesaikan dengan metode analitik. Jikapun masalah tersebut terdapat penyelesaian secara analitik, proses penyelesaian tersebut akan sangat rumit dan memakan waktu yang cukup lama sehingga tidak efisien.
Adapun kelebihan dan kekurangan dalam menggunakan metode numerik,
Kelebihan :
1. Mampu menyelesaikan persamaan diferensial non linier dan sangat kompleks
2. Mampu menghasilkan nilai perkiraan atau pendekatan dari penyelesaian analitis sehingga penyelesaian tersebut mampu memuat nilai kesalahan
Kekuragan :
1. Nilai yang didapat tidaklah eksak, melainkan berupa pendekatan
2. Perhitungannya lama dan berulang-ulang apabila permasalahannya sangat kompleks
Perkuliahan
Sebelumnya, perkuliahan metode numerik difasilitasi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. dari awal hingga Ujian Tengah Semester. Selama pengajaran oleh beliau, saya diajarkan beberapa topik metode numerik, yaitu
1. Sistem Persamaan
2. Pseudocode
3. Turunan Numerik
4. Metode Newton Rhapson, Secant, dan Bisection
5. Regresi Linier
6. Interpolasi
Setelah itu, pertemuan-pertemuan selanjutnya akan difasilitasi oleh Bapak Dr. Ir. Ahmad Indra S.
Minggu pertama (11 November 2020)
Pada minggu pertama ini, Bapak Dr. Ir. Ahmad Indra S. memberikan penjelasan terlebih dahulu mengenai apa itu metode numerik dan berbargai kegunaannya. Kemudian, beliau memperkenalkan saya kepada Wiki AIR (Ahmad Indra Research Group), salah satu media penerapan metode numerik milik beliau. Setelah itu saya juga diajarkan bagaimana cara mengakses dan menggunakan situs tersebut. Situs tersebut akan digunakan selama pembelajaran bersama beliau. Kemudian, saya dan rekan sekelas berdiskusi dengan beliau mengenai apa saja kegunaan dan manfaat mempelajari metode numerik untuk kehidupan dan pekerjaan. Berikut merupakan esensi dalam mempelajari metode numerik,
1. Memahami konsep dan prinsip dasar dalam metode numerik seperti algoritma, aljabar, persamaan diferensial, dan lain-lain
2. Mengerti dalam menerapkan dan mengaplikasikan konsep metode numerik
3. Mampu menerapkan dan mengaplikasikan metode numerik dalam persoalan teknik
4. Menempuh 3 poin diatas dengan poin terpenting, yaitu adab
Setelah itu, saya juga mendapatkan pembelajaran mengenai gambaran dasar OpenModelica, sebuah program yang berfungsi untuk menyelesaikan permasalahan yang diberikan batasan oleh kita sendiri.
Tugas 1
Minggu kedua (18 November 2020)
Pada minggu kedua, Pak Dai memberikan ajaran tentang kehidupan kepada kita bahwa janganlah menjadi orang yang merugi, jadilah orang yang beruntung. Yang dimaksud dengan menjadi orang beruntung adalah jadilah orang yang mampu menjadi pribadi yang lebih baik seiring berjalannya waktu.
Setelah itu, kami diminta untuk mempresentasikan tugas yang dikerjakan oleh masing-masing di minggu sebelumnya dengan tujuan untuk menilai kemampuan para mahasiswa dalam memahami penggunaan aplikasi OpenModelica.
Kemudian Pak Dai memberikan materi pembelajaran baru, yaitu penggunaan class untuk memanggil sebuah function. function yang bisa dipanggil kedalam beragam macamnya.
Tugas 2
Minggu ketiga (25 November 2020)
Tugas 3, trusses problem
|
Persamaan class trusses_week3 parameter Integer N=8; //Global matrice = 2*points connected parameter Real A=0.001; //Area m2 parameter Real E=200e9; //Pa Real G[N,N]; //global Real Ginitial[N,N]; //global Real Sol[N]; //global dispplacement Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; Real R[N]; //global reaction force Real SolMat[N,1]; Real XMat[N,1];
//truss 1 parameter Real X1=0; //degree between truss Real k1=A*E/1; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N]; //truss 2 parameter Real X2=0; //degree between truss Real k2=A*E/1; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N]; //truss 3 parameter Real X3=90; //degree between truss Real k3=A*E/1.25; Real K3[4,4]; //stiffness matrice Integer p3a=2; Integer p3b=4; Real G3[N,N]; //truss 4 parameter Real X4=90+38.6598; //degree between truss Real k4=A*E/1.6; Real K4[4,4]; //stiffness matrice Integer p4a=1; Integer p4b=4; Real G4[N,N]; //truss 5 parameter Real X5=90-38.6598; //degree between truss Real k5=A*E/1.6; Real K5[4,4]; //stiffness matrice Integer p5a=3; Integer p5b=4; Real G5[N,N]; /* for each truss, please ensure pXa is lower then pXb (X represents truss element number)
algorithm //creating global matrice K1:=stiffness_matrices(X1); G1:=k1*local_global(K1,N,p1a,p1b); K2:=stiffness_matrices(X2); G2:=k2*local_global(K2,N,p2a,p2b); K3:=stiffness_matrices(X3); G3:=k3*local_global(K3,N,p3a,p3b); K4:=stiffness_matrices(X4); G4:=k4*local_global(K4,N,p4a,p4b); K5:=stiffness_matrices(X5); G5:=k5*local_global(K5,N,p5a,p5b); G:=G1+G2+G3+G4+G5; Ginitial:=G; //implementing boundary condition for i in 1:N loop G[2*b1-1,i]:=0; G[2*b1,i]:=0; G[2*b2-1,i]:=0; G[2*b2,i]:=0; end for; G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1; //solving displacement Sol:=gauss_jordan(N,G,X); //solving reaction force SolMat:=matrix(Sol); XMat:=matrix(X); R:=reaction_trusses(N,Ginitial,SolMat,XMat); end trusses_week3; |
Minggu keempat (2 Desember 2020)
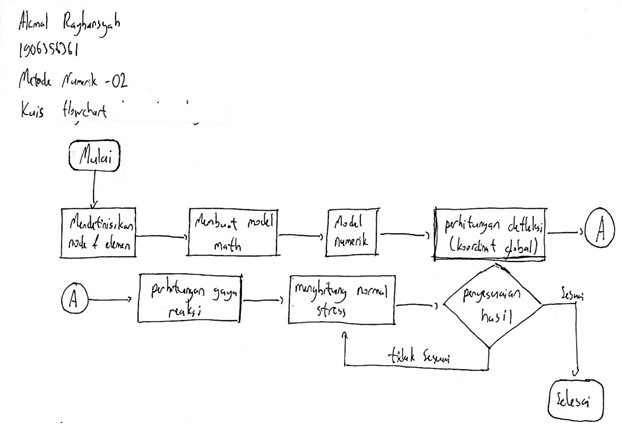
Kuis flowchart