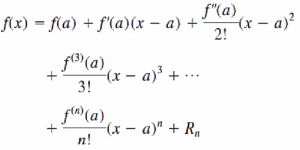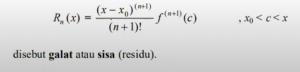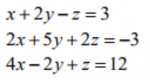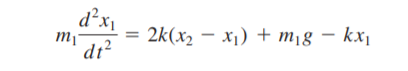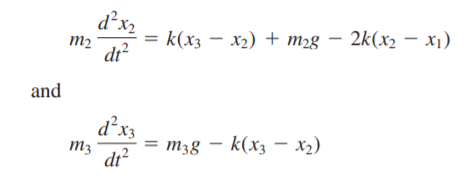Metnum03-Bolonni Nugraha
Contents
BIODATA DIRI
Nama : Bolonni Nugraha
Tempat/Tanggal lahir: Bekasi, 21 Desember 1999
NPM : 1806181741
Fakultas/ Jurusan : Teknik/ Teknik Mesin
Kelas: Metoda Numerik 03
Pertemuan 1 (9 November 2020)
Pada pertemuan kali kembali dilaksanakan secara PJJ. Pak Dai kembali mengingatkan pentingnya perhitungan secara numerik untuk membantu kita memecahkan masalah.
Berikut merupakan dasar penilaian dan objektif dari Pak Dai yang merupakan apa yang diharapkan dari setiap individu mahasiswa pada akhir semester nantinya
1. Memahami konsep, dari konsep melahirkan prinsip/pembentukan rumusan
2. Untuk menunjukan kepahaman, menerapkan konsep untuk memecahkan masalah
3. Perumusan keteknikan
4. Mendapatkan nilai tambah di dalam usaha mengenal diri sendiri
Untuk minggu pertama, Pak Dai memberikan tugas untuk menulis apa yang telah kami pelajari selama setelah semester yang lalu pada mata kuliah Metode Numerik.
Mengapa kita membutuhkan perhitungan secara numerik? Menurut Pak Engkos, selaku dosen Metode Numerik sebelum UTS, dikarenakan banyaknya perhitungan yang tidak bisa dilakukan secara eksak, khususnya perhitungan di bidang Engineering. Pendekatan Numerik menggunakan perhitungan berulang untuk mendekati nilai eksak. Berikut adalah garis besar ilmu yang saya dapatkan sebelum UTS.
1. Mencari error pada Pembulatan dan Deret Taylor
Dalam kasus khusus di mana a = 0, deret ini disebut juga sebagai Deret Maclaurin.
Deret ini merubah suatu F(x) menjadi polinomial
Errornya sendiri bukan terhadap true value, karena beberapa fungsi pada suatu titik tidak menemukan suatu nilai yang pasti, melainkan eror perbandingan value baru dengan value lama yang diabsolutkan.
2. Penyelesaian sistem persamaan
Melakukan pencarian akar-akar persamaan secara numerik. Secara garis besar dilakukan secara Brackething Method (Closed Method, menggunakan batas bawah dan batas atas), seperti pada Graphical Methods, Bisection Methods dan False-Position Methods, dan Open Method (menggunakan 1 titik), seperti pada Fixed-Point Iteration, Newton-Rapshon, dan Secant Method.
3. Regresi Linier
Regresi adalah pemodelan asosiasi antara satu variabel dependen dengan satu/lebih variabel independen. Pada kasus kali ini yang dibahas adalah pola sebaran data yang cenderung linier. Kegunaannya adalah memprediksi sebaran data selanjutnya berdasarkan data-data yang telah dimiliki sebelumnya
4. Numerical Differentiation
Pertemuan 2 (16 November 2020)
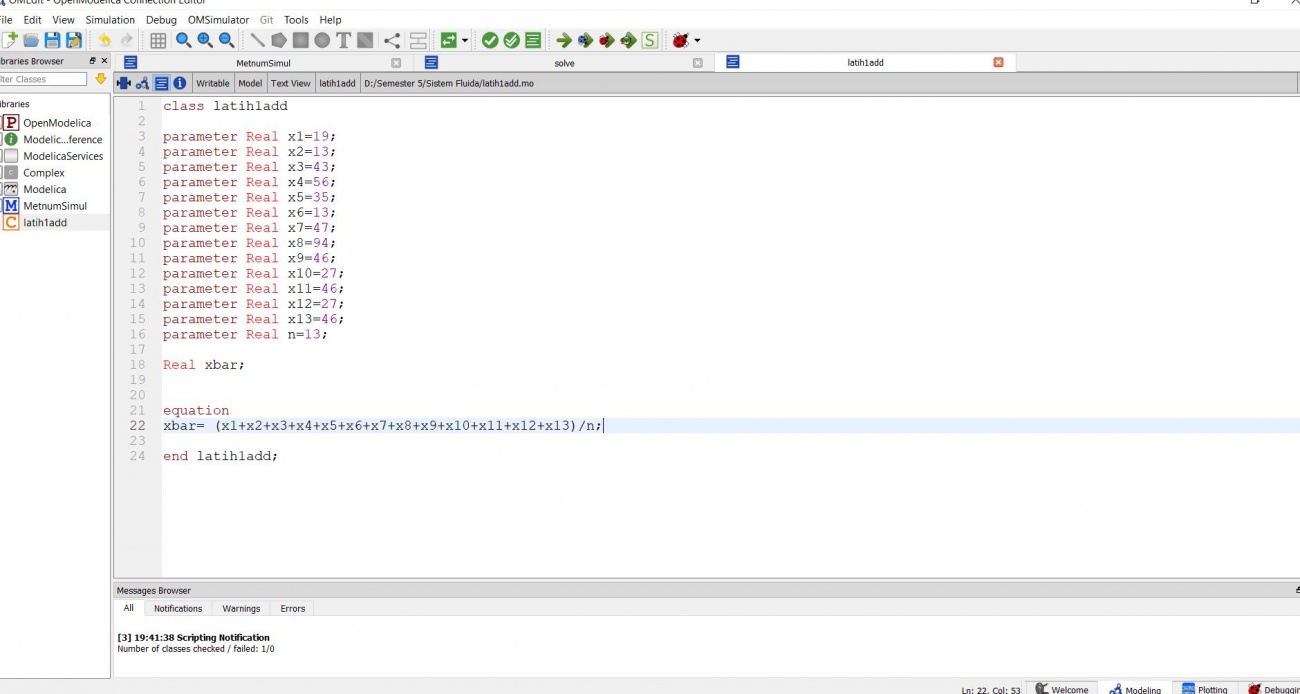
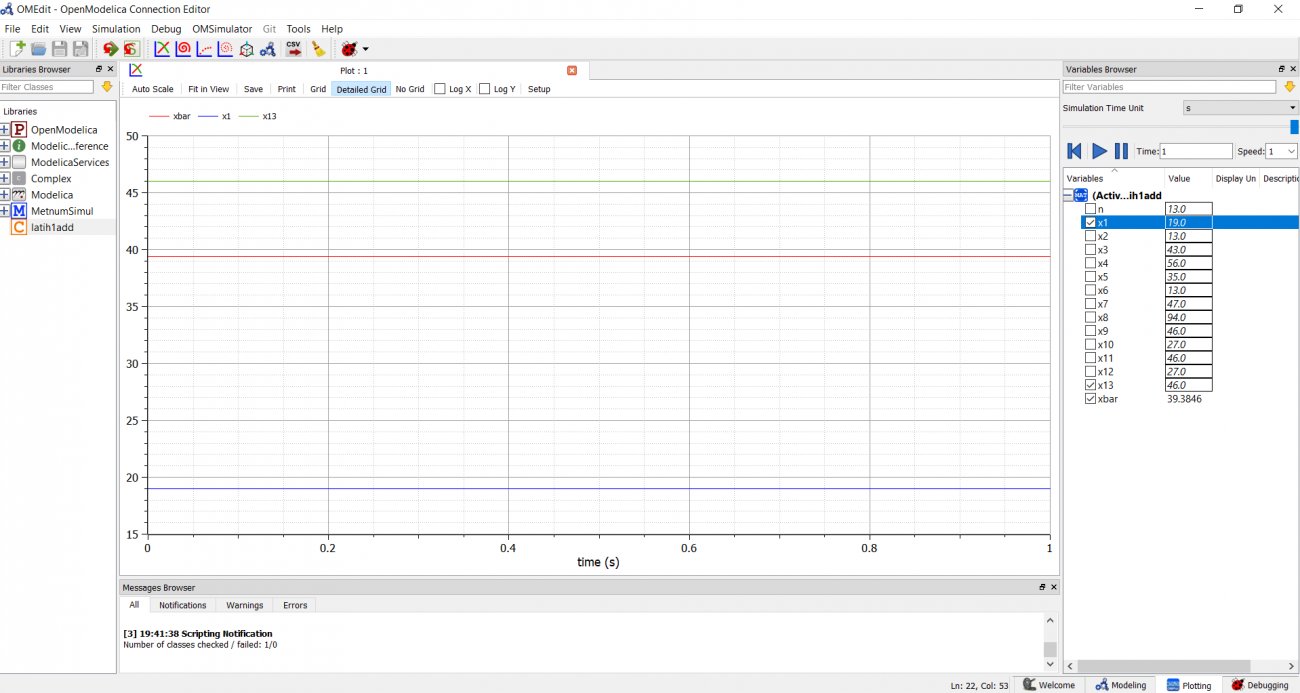
Pada pertemuan kali ini, sambil mahasiswa diminta untuk memberikan progress pembelajaran menggunakan modelica, Pak Dai meminta mahasiswa untuk mensimulasikan coding sederhana mencari nilai rata-rata dari beberapa sample. Berikut lampiran percobaan simulasi saya
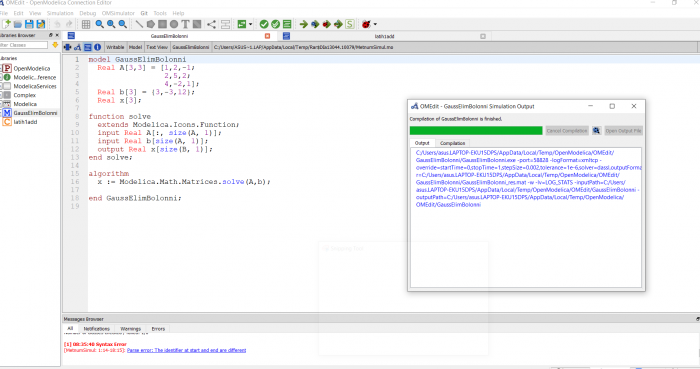
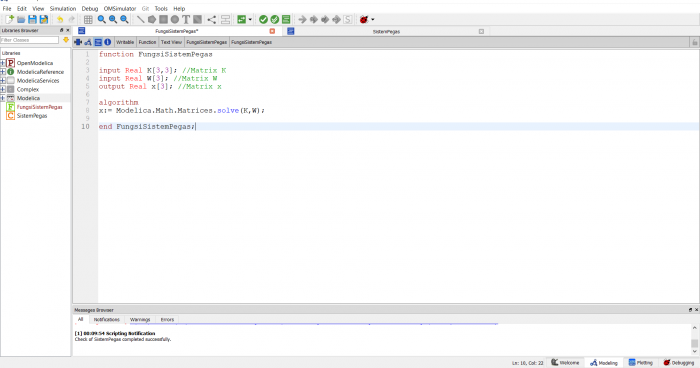
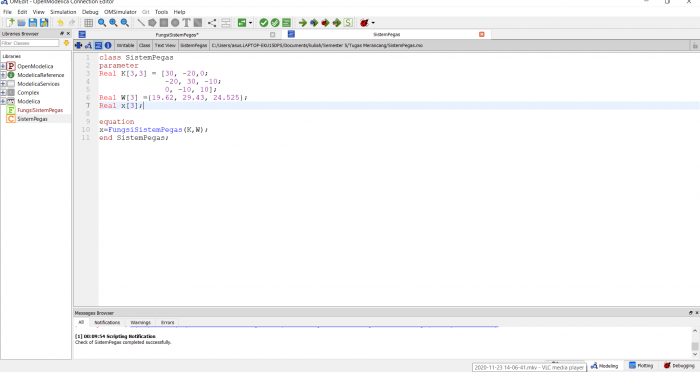
Yang berikutnya, Pak Dai juga meminta mahasiswa untuk membuat coding penyelesaian persamaan aljabar linier dengan metode yang sudah dipelajar. Disini saya menggunakan metode Gauss Elimination
Sehingga diperoleh
x=3
y=-1
z=-2
Pertemuan 3 (16 November 2020)
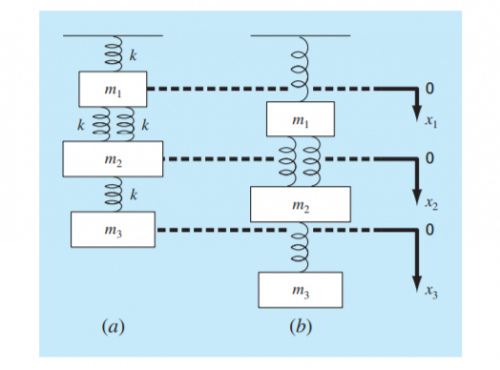
Pada pertemuan kali ini, Pak Dai menggambarkan hubungan pembelajaran kita pada kelas metode numerik dengan aplikasinya pada penyelesaian permasalahan teknik. Berikut adalah tahapan-tahapannya:
- masalah teknik
- analisis masalah
- model matematis
- model numerik
- komputer
- solusi
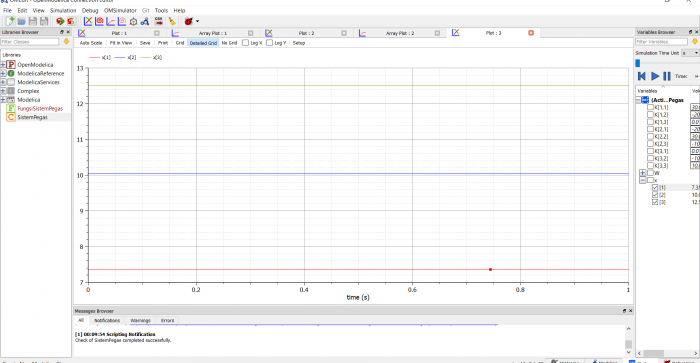
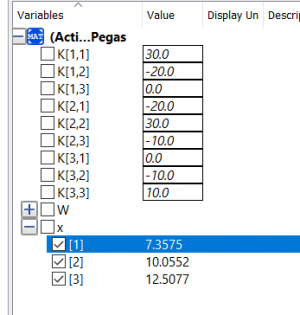
Untuk kita lebih memahami tahapan-tahapan ini, diberikan contoh kasus pada spring mass sebagai berikut: