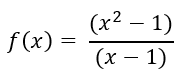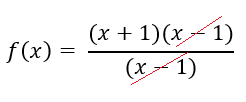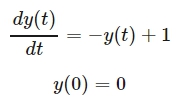Ricad Ragapati Prihandini
بِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيمِ
Saya Ricad Ragapati Prihandini, biasa dipanggil Raga/Ricad. Saya lahir di Bandarlampung, 6 Maret 1999. Saya adalah mahasiswa teknik perkapalan Universitas Indonesia semester 4. Saya mulai mengenali bahasa pemrograman sejak Saya SMA dulu. Bahasa pemrograman yang pertama kali Saya pelajari adalah bahasa pascal dimana bahasa pascal digunakan dalam soal-soal OSN komputer dalam bentuk pseudocode. Saya berlatih competitive programming di website yang disediakan oleh panitia Tim Olimpiade Komputer Indonesia yaitu TOKI Learning. Ketertarikan Saya di bidang programming melanjutkan Saya untuk mempelajari bahasa pemrograman lainnya yaitu, C++ dan Phyton. Untuk melatih dan mengembangkan ketertarikan Saya tersebut, sekarang Saya bergabung dalam tim lomba Autonomous Marine Vehicle UI (AMV UI) yaitu tim lomba yang berfokus pada pengembangan kapal tanpa awak dan remotely operated vehicle (ROV) berbasis pengolahan citra (image processing) menggunakan OpenCV. Saya berharap, dengan adanya mata kuliah metode numerik ini Saya mendapatkan banyak ilmu yang dapat saya aplikasikan dalam bidang perkapalan ini. Aamiin.
Contents
Pertemuan Pertama (7 Februari 2020)
Pada pertemuan pertama, kami diberikan pengenalan tentang mata kuliah metode numerik oleh Pak Dr. Ahmad Indra Siswantara (Pak DAI) serta kegunaannya dalam menyelesaikan permasalahan-permasalahan di bidang teknik perkapalan. Setelah itu kami mendapatkan tugas dari pak DAI untuk menyelesaikan suatu fungsi secara manual dan menggunakan program.
TUGAS MENCARI NILAI SUATU f(x)
Diberikan suatu fungsi
lalu akan dicari nilai f(x) ketika x=1
Karena apabila kita masukan nilai x=1 akan menghasilkan f(x) = 0/0 dimana dalam matematika hal tersebut disebut galat matematika/tidak terdefinisi. Maka dari itu, kita akan menggunakan metode limit dan kita perlu memfaktorkan fungsinya lalu melakukan eliminasi menjadi,
Sehingga akan menghasilkan f(x)= (x+1) dimana akan menghasilkan f(x)= 2 ketika dimasukan x=1.
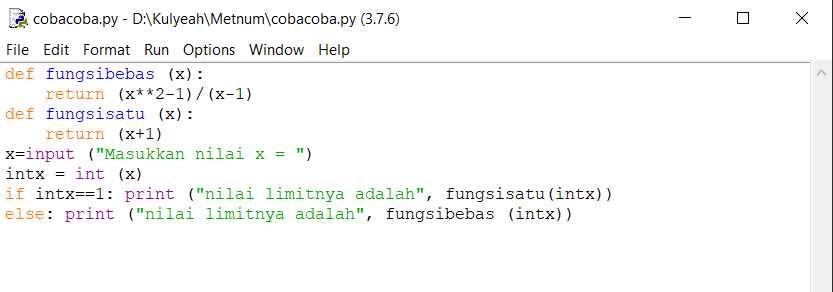
Dengan menggunakan phyton 3.8 algoritmanya seperti berikut
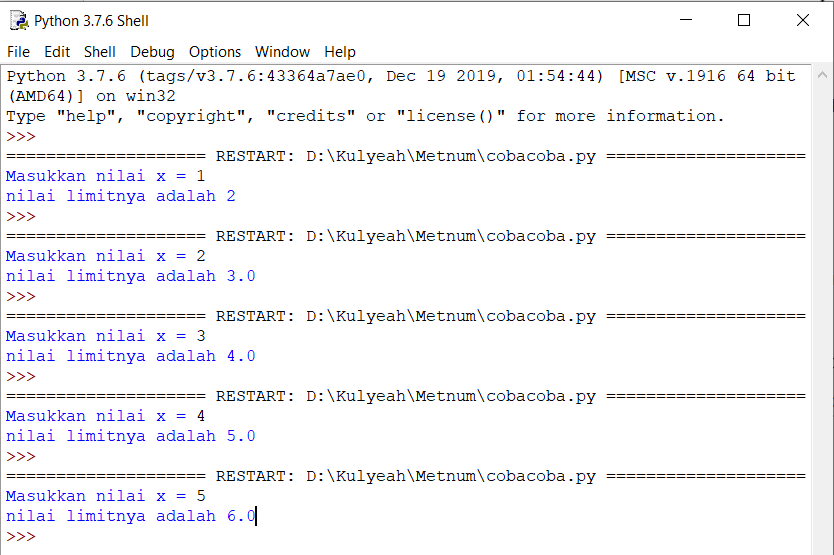
Ketika diberikan input, akan mengeluarkan output sebagai berikut:
Pertemuan Kedua (14 Februari 2020)
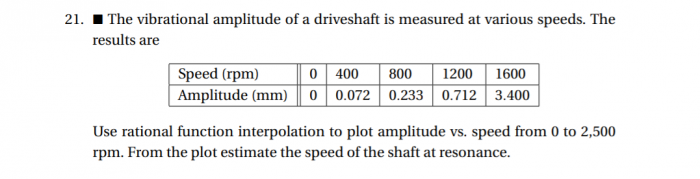
Pada pertemuan kali ini, kami diberikan kesempatan oleh pak DAI untuk memilih soal dari e-book yang telah diberikan. Kriteria soal yang dipilih berdasarkan ketertarikan setiap individu terhadap soal yang ia temukan. Menurut saya, Soal yang menarik untuk dikerjakan adalah tentang interpolasi yang biasanya Saya lakukan di Microsoft Excel.
Solusi Dengan menggunakan Python 3.8
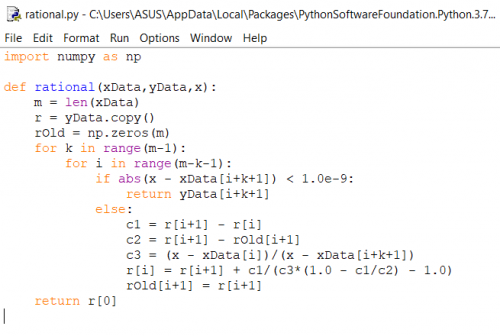
Pertama, Saya mencoba untuk mempelajari materinya terlebih dahulu menggunakan buku Numerical Methods in Engineering with Python 3 nya Jaan Kiusalaas. Kemudian, yang harus saya lakukan untuk melakukan rational interpolation adalah kita harus membuat modulenya terlebih dahulu dengan algoritma yang telah disediakan di buku. Algoritmanya adalah:
Kemudian, Saya menggunakan algoritma yang memanggil module rational terlebih dahulu untuk melakukan interpolasi sehingga Saya dapat melakukan plotting Speed vs Amplitude hingga 2500 RPM seperti yang diinginkan soal dengan bantuan library numpy yang memiliki beberapa fungsi built-in untuk membuat array baru. Saya juga menggunakan library matplotlib untuk membuat grafik hasil plottingan data Speed vs Amplitude. Algoritmanya sebagai berikut:
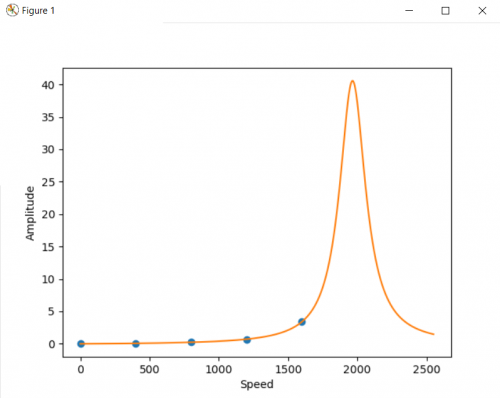
np.arange() digunakan untuk mengembalikan nilai sesuai dengan interval yang diberikan dengan parameter ([start, ]stop, [step, ]) saya menggunakan nilai step: 0.05 agar grafik data yang dihasilkan semakin smooth. Sehingga, output yang dikeluarkan adalah:
Dari data yang didapatkan, diketahui kelajuan shaft saat beresonansi adalah sekitar 1959 RPM.
INITIAL VALUE PROBLEM
Misalkan diberikan suatu masalah:
Akibat angin yang kencang, sebuah kelapa dengan massa 2 kg jatuh dari pohon dengan tinggi 15 meter.
Pertemuan Ketiga (21 Februari 2020)
Progres Belajar Metode Numerik
Setelah 3 minggu belajar metode numerik, hal yang telah saya pelajari adalah:
Asistensi I (25 Februari 2020)
Pada hari Selasa, 25 Februari 2020, kami mahasiswa teknik perkapalan yang mengambil kelas metode numerik melakukan asistensi di Lab Puskom dengan pengajar Michael Ahli. Kami diajarkan bagaimana metode runge-kutta berasal. Michael Ahli mengajarkan secara manual terlebih dahulu di papan tulis sehingga konsep-konsep utama metode runge-kutta untuk menyelesaikan persamaan diferensial. Kemudian, beliau mengajarkan untuk menulis algoritmanya di Python. Secara umum, metode runge-kutta dapat saya simpulkan sebagai berikut:
Asistensi II (3 Maret 2020)
Pada hari selasa, 3 Maret 2020, telah dilakukan asistensi mingguan namun Saya berhalangan hadir karena kondisi saya sedang sakit, untuk itu Saya bertanya ke beberapa teman saya yang mengikuti asistensi. Secara garis besar dapat disimpulkan dalam gambar berikut:
Pertemuan Kelima (6 Maret 2020)
Pada pertemuan kali ini, kami diberikan kesempatan oleh Pak DAI untuk mencari tahu perbedaan dari initial value problem dan boundary value problem. Pada kesempatan kali ini kami diberikan tugas kolaborasi untuk mengulik tentang kedua hal tersebut lalu didiskusikan melalui link berikut: Tugas Kolaborasi
Lalu, kami diberikan tugas untuk mencari contoh permasalahan dari kedua kasus tersebut.
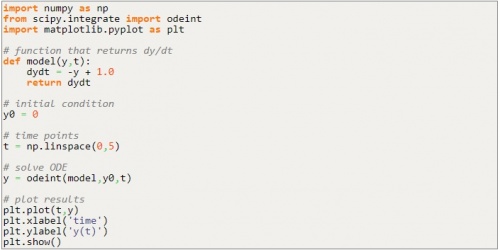
Saya pun menemukan suatu contoh initial value problem yaitu: Diberikan suatu model matematis dengan persamaan
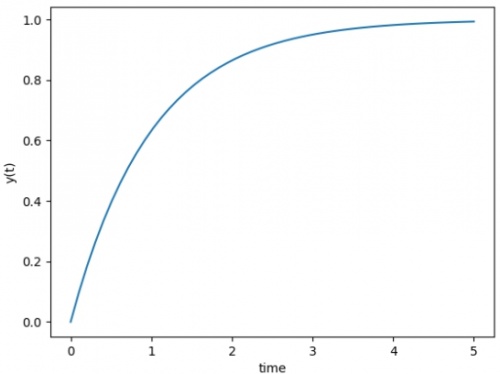
Kemudian mencari solusi numericalnya menggunakan python dan melakukan plotting untuk mencari dimana fungsi tersebut mulai mencapai keadaan steady state
Saya menemukan cara yang lebih praktis untuk menemukan solusi dari initial value problem maupun boundary value problem menggunakan library ODEINT.
Pertemuan Keenam (13 Maret 2020)
Pada pertemuan kali ini, kami diajarkan tentang Metode Optimasi menggunakan python oleh bang Edo karena pak DAI sedang sakit (Syafakillah pak, Aamiin). Metode optimasi ini digunakan untuk mengoptimasi atau mencari nilai yang optimal dari suatu persamaan yang telah dibuat dengan memasukan batas-batas yang disebut constraint agar hasil yang didapatkan mempunyai error yang kecil. Pada pertemuan ini, kami diberikan intermezzo tentang optimasi dengan contoh persamaan linier sederhana. Kami justru malah banyak belajar hal-hal dasar python mulai dari array dan indeksnya, mendefinisikan fungsi, looping dll Terimakasih bang Edo.
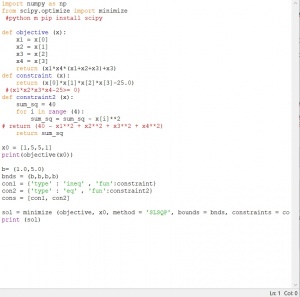
Dapat dilihat bahwa tujuan optimasi tersebut untuk mencari nilai maksimum x1,x2,x3,x4 yang memenuhi persamaan x1*x4*(x1+x2+x3)+x3 dengan constrain:
1. x1*x2*x3*x4=25 dan
2. x1^2+x2^2+x3^2+x4^2 = 40
Serta nilai awal untuk mencoba-coba adalah x1=1, x2=5, x3=5, x4=1, dimana nilai x1,x2,x3,x4 berada pada rentang {1.0,5.0}
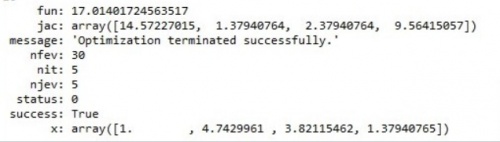
Setelah dijalankan, program mulai melakukan optimasi dengan algoritma di atas, didapatkan hasilnya yaitu nilai x1=1.0, x2= 4.7429961, x3= 3.82115462, x4= 1.37940765.
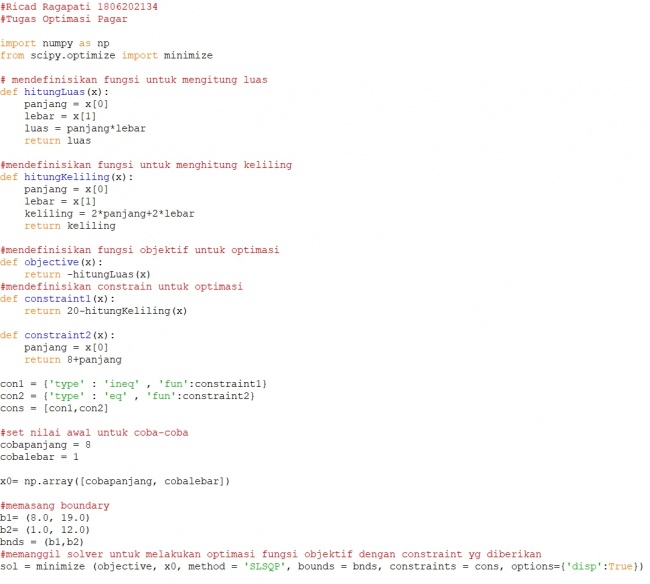
TUGAS OPTIMASI LUAS HALAMAN Setelah dilakukan pengenalan tentang optimasi, Bang Edo memberikan tugas yang diamanahkan pak DAI kepadanya untuk mencoba melakukan optimasi dengan kasus sebagai berikut:
Diberikan kayu sepanjang 20m, lalu kita harus mengoptimasi panjang dan lebar kayu untuk mendapatkan luas halaman maksimal. Constraint yang diberikan adalah panjang kayu 20m yang akan menjadi keliling halaman. Kemudian, constraint selanjutnya yaitu panjang dari halaman harus lebih dari 8m. Untuk itu, dilakukan optimasi menggunakan python dengan algoritma sebagai berikut:
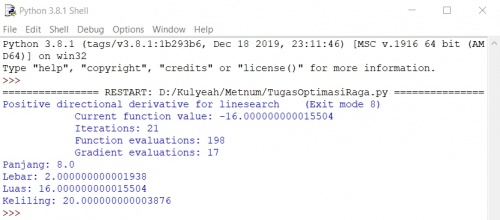
Kemudian, dilakukan run module dan mengeluarkan output sebagai berikut:
Didapatkan bahwa panjang optimal adalah 8.0 m dan lebar 2.000000000001938m sehingga luasnya menjadi 16.000000000015504 m^2 dan memenuhi constraint bahwa kelilingnya 20.000000000003876 m.