Tugas 5 Vinia Permata Kusuma
Contents
Tugas 5 Metode Numerik
Pada Pertemuan ke-5 tugas yang diberikan adalah menyelesaikan initial dan boundary value problem
Initial value problem
sistem rekayasa dengan pegas linier, s (u) = kx, dan peredam kental, di mana gaya peredam proporsional dengan u ′, f (u ′) = bu ′, untuk beberapa konstanta b> 0. Persamaan ini dimodelkan sistem pegas vertikal dalam mobil . Kita dapat memilih nilai-nilai sederhana untuk konstanta untuk mengilustrasikan efek dasar redaman (dan kegembiraan selanjutnya). Memilih osilasi sebagai fungsi u (t) = nilai fungsi kasus undamped, kita dapat menetapkan m = 1, k = 1, b = 0,3, U0 = 1, V0 = 0. Fungsi berikut mengimplementasikan kasus ini:
Boundary Value Problem
Kita ambil dari data kapal selam yang dicari di kecepatan 11,15, dan 20
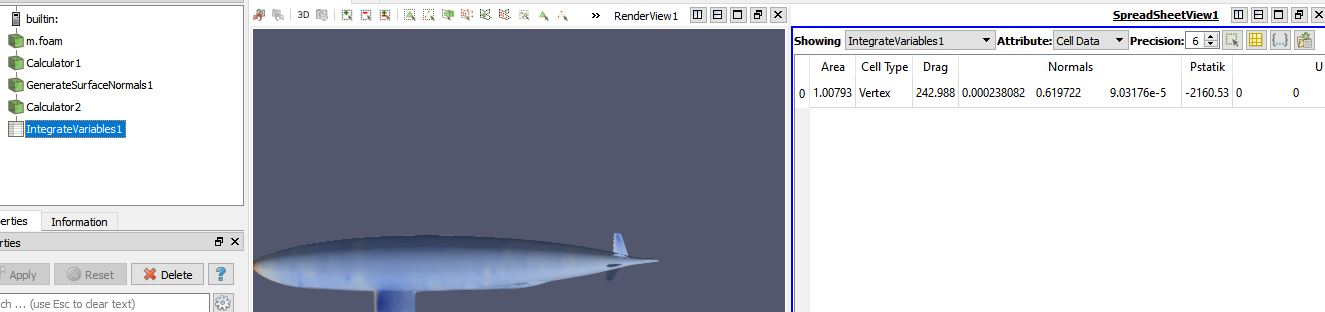
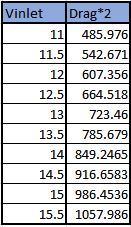
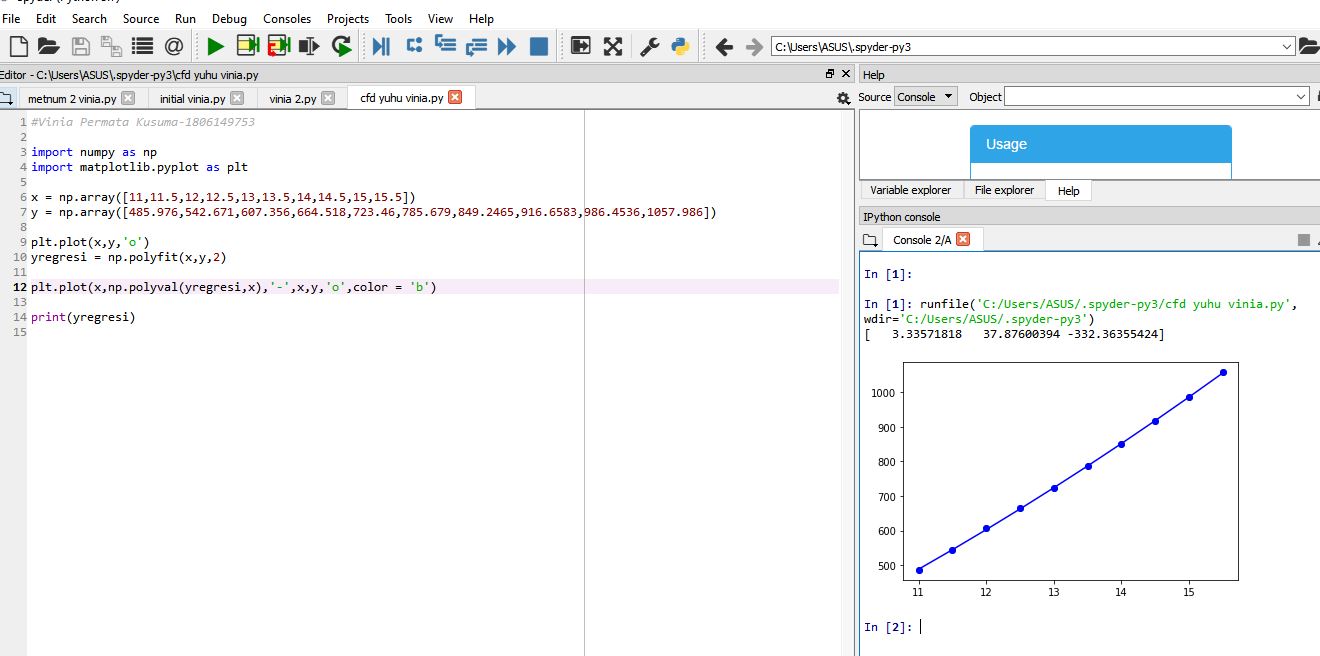
Komentar
Dalam menghitung hambatan kapal Membutuhkan kesabaran yang banyak untuk merubah kecepatan dan menunggu grafik pada CFDSOF dan dapat kita koreksi kecepatannya dengan regresi linier di phyton