Adhika Satyadharma

Biodata

Nama  : Adhika Satyadharma

NPM  : 1906323956

Jurusan  : Teknik Mesin - Konversi Energi

Info Lain : -

Komputasi Teknik - Pendahuluan

1.1. Apa itu Komputasi Teknik?

Komputasi teknik merupakan sebuah teknik mengunakan tenaga komputer untuk menyelesaikan masalah-masalah teknik. Hal ini dilakukan karena dengan menggunakan komputer, masalah dapat selesai dengan lebih cepat, mudah sehingga (seperti biasa) pada akhirnya cost engineeringnya akan berkurang.

1.2. Tahap-Tahapan Komputasi Teknik

Untuk menyelesaiakan masalah teknik yang dibantu oleh tenaga komputer ada berberapa tahap yang perlu diikuti, yaitu:

1. Pahami masalah yang perlu diselesaikan.

2. Terjemahkan masalah tersebut kedalam bahasa yang dimengerti oleh komputer.

3. Biarkan komputer memproses informasi yang ada.

4. Setelah komputer mengeluarkan hasil, maka hasil ini harus selalu dicheck ulang oleh engineer.

1.3. Apakah Komputasi Teknik Penting Dipelajari?

Komputasi teknik menurut saya merupakan hal yang penting untuk diketahui oleh orang teknik, khususnya mahasiswa/peneliti. Hal ini dikarenakan sering kali ada suatu kasus (persamaan matematis) yang tidak dapat diselesaikan dengan mudah sehingga dibutuhkan skill-skill lebih lanjut (komputasi teknik) untuk menyelesaikannya. Tanpa kemampuan ini seseorang akan sangat bergantung pada aplikasi-aplikias tertentu, dan terpaksa mengikuti persyartan dan keterbatasan aplikasi tersebut, dimana belum tentu sesuai dengan apa yang ingin diselesaikan.

1.4. Kemampuan Saya dalam Komputasi Teknik

Pengalaman saya dengan komputasi teknik sudah cukup banyak. Saya telah melakukan perhitungan untuk menyelesaikan masalah-masalah teknik selama cukup lama. Sebagai contoh dalam berberapa hari terakhir saya membuat perhitungan yang memfilter dan mengolah hasil CFD dalam excel. Contoh lain adalah saya telah membuat program yang menghitung propagasi error dalam CFD (Computational Fluid Dynamics) menggunakan bahasa Phyton. Contoh lain lagi adalah saya pernah membuat program pengolahan hasil PIV (Particle Image Velocimetry) dalam matlab, sekalipun yang ini hasilnya masih kurang robust. Masih ada banyak contoh lain tentang aplikasi yang pernah saya lakukan seperti: Program curve fitting (phython, matlab), Program untuk membantu pembuatan mesh multiblock (excel), program linear equation solver (implicit)(phython), program test mesh independency (phython, matlab, excel). Selain itu saya juga sudah sangat biasa mengoperasikan fluent, dimana fluent merupakan program CFD dan CFD merupakan sebuah program yang didalamnya ada sangat banyak teknik komputasi.

Sumber : Pendapat Pribadi

Project Komtek - Latar Belakang

Sebelumnya saya ingin menyampaikan bahwa topik yang akan saya sampaikan disini bukanlah skripsi saya. Skripsi saya membahas masalah plasma aktuator pada plat datar, dimana memang salah satu komponen penelitiannnya adalah simulasi MHD dengan fluent. Namun seingat saya salah satu poin dari tugas ini adalah untuk dibuat karya ilmiah. Skripsi saya sudah pernah saya presentasikan dalam confrence terdahulu oleh karena itu saya tidak akan menyampaikan materi mengenai skripsi saya disini, namun suatu kasus lain yang baru saja saya kerjakan, dan fokusnya memang pada masalah komputasi teknik.

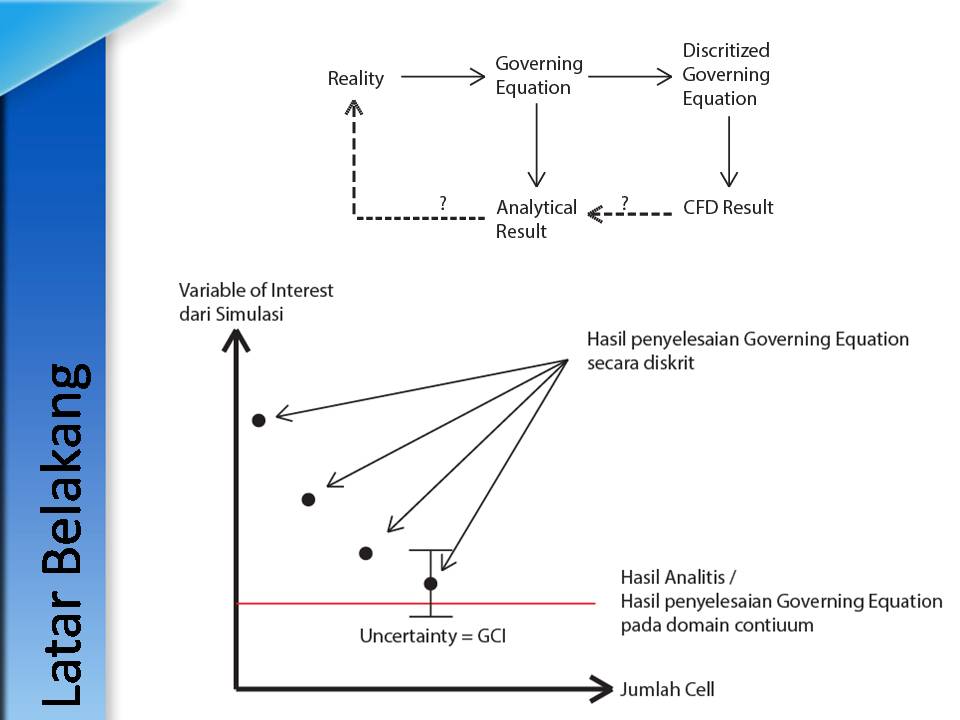
Kasus yang saya akan jelaskan disini terkait dengan masalah error-error pada CFD. Dalam CFD terdapat berbagai jenis error, dimana salah satunya adalah numerical error yang didalamnya mengandung error-error lain seperti iterative error, round-off error, dan error diskritisasi. Dalam verifikasi kasus CFD biasanya penekanannya lebih diutamakan kepada error diskritisasi, yaitu karena biasanya dampakanya paling besar.

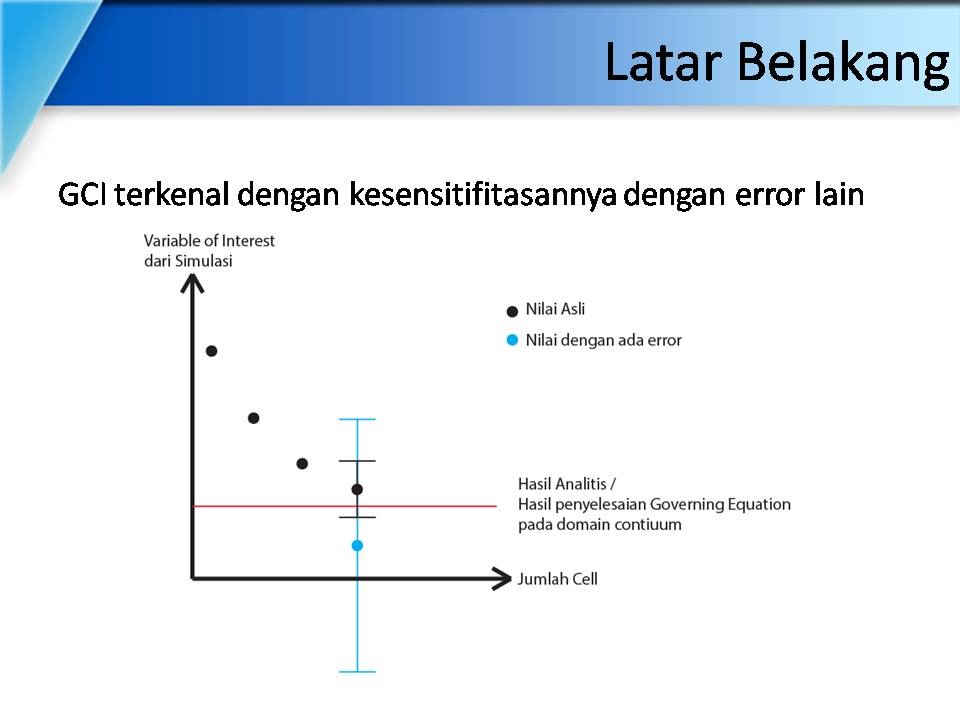
Error diskritisasi dalam CFD biasa dikalkulasikan dengan sebuah teknik bernaman Grid Convergence Index (GCI). Hanya saja salah satu masalah dengan metode ini adalah diasumsikannya bahwa tidak ada error lain dalam datanya. Apabila sebuah data yang mengandung error diolah menjadi GCI, maka error ini akan ikut terpopagasi sehingga hasil analisa error diskritisasinya menjadi kacau. Oleh karena itu, error iterasi dan round off error perlu diminimalisir sedemikian rupa sehingga bahkan saat terpopagasi efeknya tidak signifikan.

Mengenai batasan maximum dari iterative dan round-off error, dari paper-paper yang saya baca ada berbagai pendapat mengenai batas ini.

- Celik (2008) (Panduan verifikasi ASME) mengatakan bahwa batas maximumnya adalah 1 orde of magnitude dari error diskritisasi

- Roy (2005) mengatakan bahwa batas maximumnya adalah 2 orde of magnitude dari error diskritisasi

- Eca & Hoekstra (2009) mengatakan bahwa batas maximumnya adalah 2-3 orde of magnitude dari error diskritisasi

Hanya saja diantara pendapat-pendapat ini hanya Eca & Hoekstra saja yang memberi alasan detail mengenai rekomendasinya. Mereka menggunakan berberapa study case untuk memberi rekomendasi mengenai batas mereka, sedangkan yang lain tidak memberi alasan.

Dalam karya ilmiah ini, saya berusaha mencari bukti tambahan mengenai batas maksimal ini. Adapun cara yang saya gunakan adalah memodelkan efek error iterasi dan round off error pada perhitungan GCI dan mencobanya pada range data yang cukup luas. Sayangnya karena kalkulasi GCI sendiri butuh perhitungan numerik dan model yang terbentuk cukup rumit sehingga sulit dikalkulasikan secara analitik, maka proses perhitungan diserahkan sepenuhnya pada komputer.

Refrence

I. B. Celik, et al. Procedure for estimation and reporting of uncertainty due to discretizationin CFD applications. J. Fluids Eng., 130:078001, 2008.

Roy, C. J. (2005). “Review of code and solution verification procedures for computational simulation,” Journal of Computational Physics, Vol. 205, pp. 131-156.

Eca, L., and Hoekstra, M. (2009). “Evaluation of numerical error estimation based on grid refinement studies with the method of the manufactured solutions,” Computers & Fluids, Vol. 38, pp. 1580-1591.

Project Komtek - Slide

Project Komtek - Extended Abstract

(Sekalipun abstract diminta diupload ke grup WA, saya akan upload disini terlebih dahulu. Apabila ada revisi maka akan saya upload lagi)

Judul: Batasan Error Iteratif dan Error Round-Off dalam Perhitungan Grid Convergence Index untuk Verifikasi Hasil Computational Fluid Dynamics

Dalam CFD terdapat 4 tahap yang perlu dilakukan yaitu pemodelan, diskritisasi, perhitungan, dan verifikasi dan validasi. Diantara keempat tahap ini, hanya 3 tahap yang pertama yang perlu dilakukan untuk mendapat hasil, sedangkan verifikasi dan validasi merupakan proses untuk memastikan kebenaran dari hasil yang didapat. Terkhusus pada bagian verifikasi, salah satu teknik yang sering digunakan adalah Grid Convergence Index (GCI). Teknik ini digunakan untuk mengestimasi error diskritisasi spatial dari hasil CFD, dimana error ini nilainya cenderung besar. Hanya saja masalah dengan metode ini adalah bahwa metode ini mempunyai sifat yang sensitif, dimana apabila data yang digunakan dalam perhitungannya mengandung error, terkhusus error iteratif dan round-off error, maka hasil yang diberikan dapat berbeda jauh. Untuk mengetahui seberapa besar error yang dapat diterima oleh metode GCI, sebuah perhitungan analitis dilakukan. Perhitungan ini dilakukan dengan memodelkan dampak error iteratif dan round-off error pada perhitungan GCI. Adapun model ini diuji pada range 1 < r12, r23, f2/f1, f3/f1 < 2, serta error iteratif dan round-off error dalam range 0.0001% to 10%. Seluruh perhitungan ini dilakukan secara diskrit menggunakan program yang dibuat sendiri. Dari hasil perhitungan ini, ditemukan bahwa error iteratif dan round-off error harus berada 3 hingga 4 order of magnitude lebih kecil dari error diskritisasi yang diharapkan.