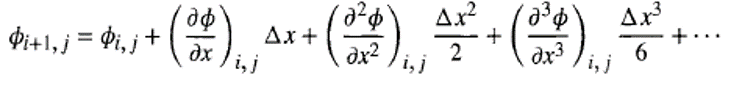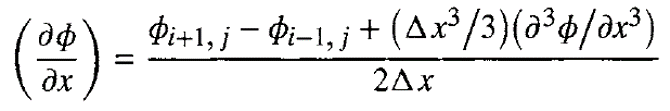Muhammad Hilman Gumelar Syafei

بِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيم 

Informasi Singkat

Alhamdulillah, segala puji bagi Allah Ta'ala, atas karunianya saya bisa membuat page di wiki ini. Shalawat serta salam senantiasa kita ucapkan kepada nabi Muhammad Shalallahu 'alaihi wasallam Perkenalkan, nama saya Edo, Informasi singkat mengenai saya bisa dilihat sebagai berikut:

Nama  : Muhammad Hilman Gumelar Syafei

Pendidikan Terakhir : Teknik Mesin - Sarjana

Email  : edoalbamusic@gmail.com

No. HandPhone  : 087889337317

TOPIK RISET  : Pengembangan Teknologi FCC (Fluid Catalytic Cracking) pada aplikasi Zero Energy Building

Insyaa Allah di page ini, saya akan berbagi informasi mengenai aktivitas studi dan penelitian saya. Saya dengan senang hati menerima kritikan dan masukan dari teman-teman semua. Semoga bermanfaat :D

Aktivitas

Saat ini, saya sedang aktiv mengambil kuliah magister Jurusan Teknik Mesin di Universitas Indonesia, dengan bidang peminatan Konversi Energi. Tema penelitian yang saya adalah aplikasi Zero energy Building, dan topik penelitian saya adalah optimasi desain turbin spiral Archimedes. Selain itu saya juga sedang aktif menjadi asisten kelas metode numerik dan meberikan pelatihan simulasi CFD . Materi dari kelas metodu numerik dapat dilihat pada page dibawah ini:

PYTHON - Kelas Metode Numerik CFDSOF-NG

Study dan Penelitian

Untuk menunjang penelitian yang saya lakukan di perkuliahan magister teknik mesin, saya melakukan beberapa study, diantaranya seperti Penggunaan Python untuk aplikasi metode numerik, kemudian mendalami kembali persamaan-persamaan dasar mekanika fluida, optimasi, dan sebagainya. Selama perkuliahan magister ini, rencanya semua materi-materi yang dipelajari akan dimuat di wiki ini. Sehingga, diharapkan dapat terdokumentasi dengan baik.

Publikasi Ilmiah

Saat ini, saya sudah menghasilkan beberapa publikasi ilmiah selama saya menjalani studi saya di S1 teknik mesin Universitas Indonesia. Untuk inofrmasi lebih lanjut, dapat dikunjugi laman berikut : Publikasi ilmiah

CATATAN PERKULIAHAN

Alhamdulillah segala puji bagi Allah subhanahu wata’ala, atas nikmat dan karunia-Nya, saya bisa kembali menulis dan memperbaharui tulisan saya di wiki ini. Shalawat serta salam senanatiasa di panjatkan kepada nabi akhir zaman, nabi kita tercinta, yang dengan perjuangan beliau, kita sekarang bisa merasakn terangnya ilmu, sehingga kita bisa terhindar dari kebodohan.

Alhamdulillah, sekarang saya sedang menjalani perkuliahan S2 di teknik mesin Universitas Indonesia dan, atas nikmat dan karunia Allah subhana hu wata’ala, saya bisa mendapatkan beasiswa. Sampailah saya di salah satu mata kuliah yang diampu oleh dosen yang sudah saya kenal sangat dekat, bahkan menjadi pembimbing saya di perkuliahan, yaitu Dr. Ir. Ahmad Indra Siswantara, atau yang akrab disapa dengan pak DAI. Sudah menjadi ciri khas beliau bahwa setiap mahasiswa yang hadir didalam mata kuliah nya, didorong untuk senantiasa mendokementasikan hasil kegiatan belajar mereka di dalam sebuah tulisan yang nantinya akan di muat pada laman wiki ini. Sehingga, setiap mahasiswa diharapkan dapat saling berbagi pendapat dan pengetahuan. Selain itu, hasil pembelajaran selama satu semester juga diharapkan dapat menjadi bahan belajar yang bermanfaat bagi orang lain.

KOMPUTASI TEKNIK

--pertemuan-1 : 03-02-2020--

Di pertemuan pertama di hari perkuliahan, beliau menyampaikan tujuan mempelajari komputasi teknik. Dari yang saya catat dan saya pahami, tujuan mempelajari komputasi teknik yang pertama adalah memahami konsep-konsep dan prinsip-prinsip didalam pelajaran komputasi teknik, yang mencakup sebagai berikut:

-Komputasi teknik : suatu kegiatan operasi aritmetik (tambah, kali, bagi, kurang) angka angka tadi.

-Kalkulasi enginering menggunakan komputer.

-Didalam istilah-isitlah komputasi teknik, banyak konsep-konsep yang harus dipahami. Pertama, konsep iterasi, kemudian, konsep error. Error sendiri terdiri dari beberapa jenis, ada residual error, dll. Jadi ada sebuah batasan error. Kemudian ada konsep convergen, konsep verifikasi dan validasi serta perbedaan keduanya.

-Metode-metode untuk mengolah data, misalnya untuk mengolah data seperti regresi, dan lain-lain.

-Contoh aplikasi metode numerik, misalnya memperkirakan persebaran temperatur ada sebuah plat dengan sebuah persamaan yang dimodelkan dengan :

2T1 + 3T2 + T3 = 5T4 5T1 - 2T2 + 5T3 = 7T4

-pada masalah-masalah engineering, terdapat banyak persamaan-persamaan model matematis yang harus diselesaikan, msialnya menyelesaikan sistem persamaan dengan menggunakan matrix yang dapat di selesaikan dengan komputer.

Lalu, tujuan mempejari komputasi teknik yang kedua adalah dapat memahamkan konsep-konsep disebutkan pada point 1 untuk aplikasi teknik mesin. Hal ini menruut saya sangat penting. Karena kita berharap bahwa ilmu yang akan kita pelajari ini nantinya menjadi ilmu yang bermanfaat dan dapat diamalkan. Sebagaimana nasihat emas dari Al- Imam Asy-Syafi’i Rahimahullah :

“Ilmu adalah yang bermanfaat dan bukan hanya dihafalkan” (Siyar A’lamin Nubala, 10: 89).

baca tulisan lengkapnya di Rumaysho: [1]

*Qadarallah, pada pertemuan ke 2 hingga ke 4, saya berhalangan hadir

Tugas Susulan

Pengertian Analisa Kata analisa dapat diambil pengertiannya dari kamus besar bahasa Indonesia, yaitu dari kata analisis yang didefinisikan sebagai penyelidikan terhadap suatu peristiwa (karangan, perbuatan, dan sebagainya) untuk mengetahui keadaan yang sebenarnya (sebab-musabab, duduk perkaranya, dan sebagainya). Namun, didalam bidang teknik, beberapa rekan dari kelas komputasi teknik juga memberikan definisi yang berbeda-beda, diantaranya adalah sebagai berikut: 1. Ilham Bagus waranto : pemecahan suatu masalah yang kompleks sehingga menjadi lebih mudah dipahami 2. Adzana Moslem : aktivitas yang dilakukan untuk mengurangi suatu permasalahan atau kasus 3. Evi Elisha : pemahaman atau pengkajian lebih dalamakan suatu hal. 4. Muchalis : suatu proses untuk menyelesaikan suatu masalah dan menghasilkan kesimuplan. 5. Ahmad Zikri : suatu penyilidikan terhadap persitiwa untuk mengetahui suatu kebenaran.

Demikian, analisa menurut pandangan saya adalah  : Sebuah usaha untuk menilai dan mengamati suatu permasalahan berdasarkan pemahaman yang dimiliki untuk menghasilkan sebuah kesimpulan atau dugaan

Catatan Ringkasan Computational Fluid Dynamics

1. Pendahuluan

Awal mulanya, CFD digunakan terbatas hanya pada aplikasi keteknikan berteknologi tinggi di aeronotika dan astronotika.

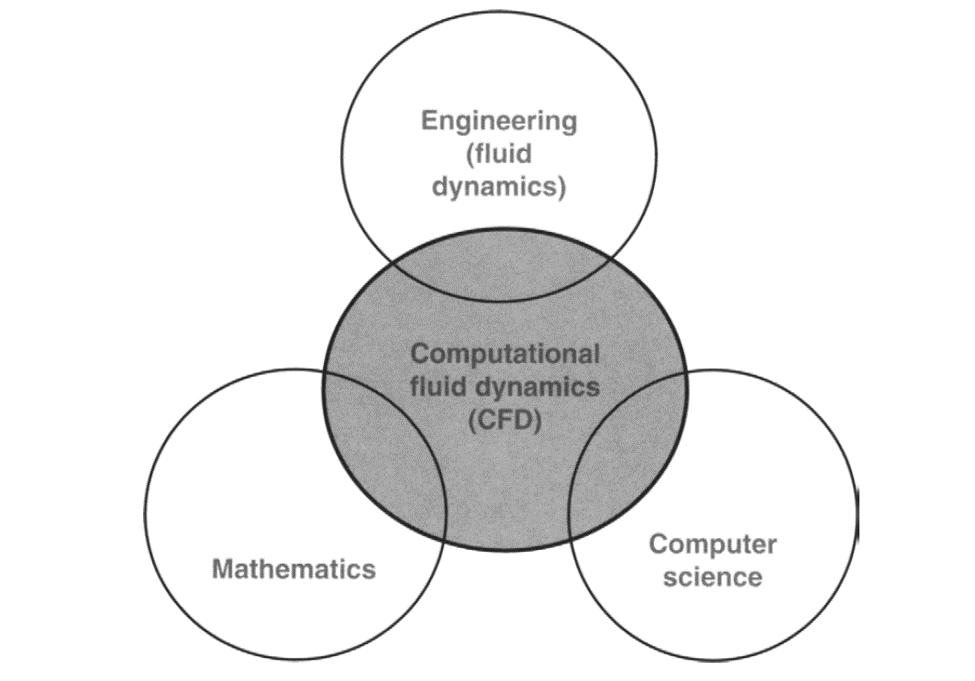
-> CFD merupakan cabang disiplin ilmu yang mengintegrasikan mekanika fluida, matematika, dan ilmu computer. Mekanika fluida, mempelejari fluida yang bererak maupun diam, serta pengaruh perilaku aliran terhadapa perpindahan panas dan reaksi kimia seperti pada pembakaran.

-> Lalu, karakteristik fisk dari gerak fluida tersebut dapat di deskripsikan melalui persamaan matematika dasar, umumnya merupakan bentuk persaaan partial differential yang mengatur proses tersebut dan biasanya disebut dengan governing equation.

-> untuk menyelesaikan governing equation tersebut, ilmuwan di bidang ilmu komputer menggunakan bahasa pemrograman tingkat tinggi untuk menyelesaikannya, dan kemudian menjadikannya sebuah program atau software. Secara sederhana, makna computational pada CFD berarti study mengenai aliran fluida melalui simulasi numerik, yang mana melibatkan pemanfaatan software pada komputer.

-> Pertanyaannya, apakah kita memerlukan orang-orang dari 3 disiplin ilmu tersebut secara spesifik. Jawabannya adalah tidak, karena orang yang mahir dalam mempelajari ilmu CFD ini justru akan mendapatkan ilmu-ilmu yang ada di 3 disiplin ilmu tersebut.

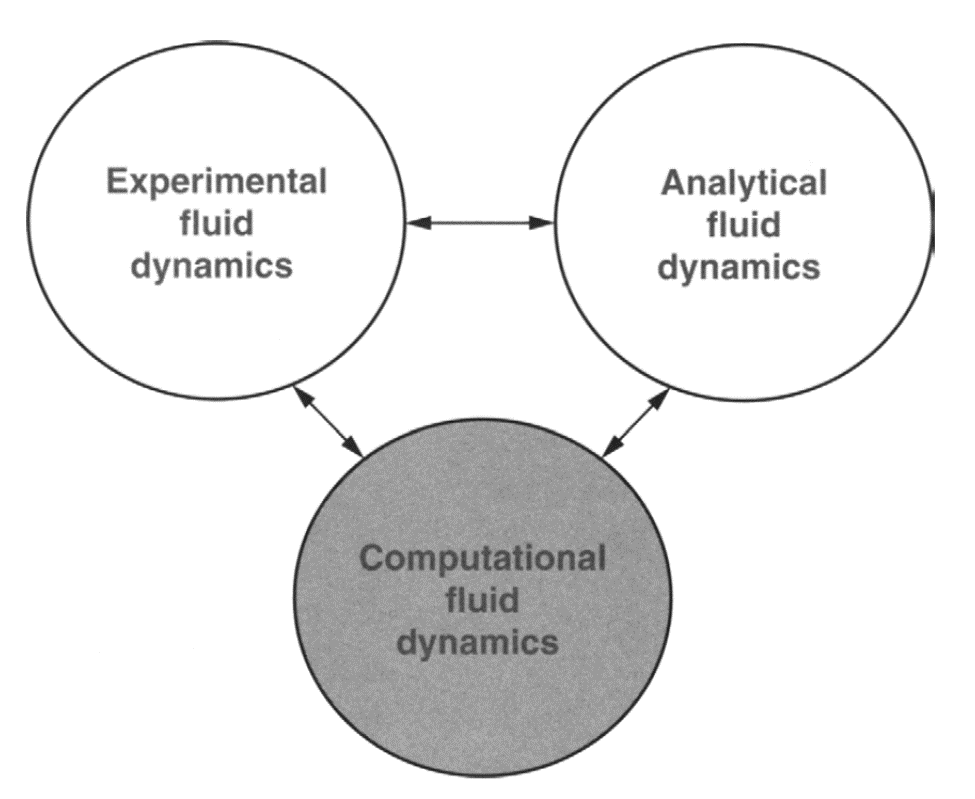
-> CFD menjadi salah satu dari 3 cara untuk solusi dari suatu masalah pada fluid dynamic and heat transfer. Dan 3 cara tersebut saling berkaitan dan tidak saling terpisah/terisolasi, yaitu analytical, experimental, dan numerical computational.

-> saat dahulu, orang-orang yang mendalami ilmu CFD akan menyisihkan waktu mereka untuk menulis code program computer mereka sendiri. Namun demikian, dengan semakin bertambahnya permintaan dari Industri dan bahkan juga di dalam akademis yang menginginkan pengetahuan mengenai CFD dengan waktu yang singkat (tidak terlalu lama), maka tidak asing lagi bahwa orang-orang mulai banyak yang mengabaikan untuk menulis code programnya masing-masing, terlebih lagi dengan meningkatnya penggunaan software CFD secara commercial yang tersedia. Multi purpose software CFD mulai banyak di terima secara luas, terutama karena model-model yang telah berkembang dan dapat merangkum fenomena aliran fluida secara fisik. Selain itu, penulisan code program CFD sudah banyak dilakukan dan di uji dengan pihak-pihak pengembang software tersebut, maka di saat ini, pengguna CFD tidak lagi menghadapi persoalan-persoalan semacam itu, karena program-program yang telah berkembang saat ini dapat digunakan untuk berbagai persoalan aliran fluida.

-> Akan tetapi, CFD bukanlah semata-mata hanya mahir dalam menggunakan software dan semacamnya. Hal yang penting dalam mempelejari ilmu CFD (khususnya yang akan disediakan buku ini) adalah mempelajari ilmu CFD secara lebih bijakssana, yaitu memberikan pemahaman mengenai pokok konsep dasar dan mengetahui "Know-How" (atau alasan-alasan) untuk menangani masalah masalah aliran fluida.

-> beberapa referensi bagi yang ingin mendalami atau melakukan riset mengani pengembangan model matematika dapat melihat buku-buku seperti (Fletcher,1991, Anderson, 1995, Versteeg dan Malalakasera,1995).

CFD Technique

-> Secara umum, terdapat teknik dasar komputasi yang digunakan untuk mencari solusi dari governing equation dari permasalahan fluid dynamic dengan boundary condition yang tepat sesuai dengan kasus spesifik tersebut. ->Proses untuk mendapatkan solusi komputasi (computational solution) terdiri dari 2 tahap. Tahap pertama yaitu meliputi konversi persamaan diferensial parsial dan auxiliary(boundary and initial) condition menjadi sebuah sistem persamaan linier aljabar diskrit (system of discrete algebraic equations). Langkah ini disebut dengan langkah diskritisasi (discretization stage). -> Pada bab sebelumnya, telah dibahas bagaimana menyelesaikan persamaan governing equation secara analytical. Namun pada kondisi realnya, kondisi aliran adalah 3 dimensi. Sehingga penyelesaiannya sangat kompleks dan tidak mudah. Bahkan, walaupun aliran disederhanakan disederhanakan menjadi aliran 2 dimensi, governing equation akan tetap diselesaikan secara analitik.

-> Oleh karena itu, dari pada menyelesaikan persamaan governing equation dan mendapatkan nilai parameter-parameter simulasi seperti u,v,w,p, dll yang diselesaikan dengan sebuah fungsi eksplisit tertutup (closed-form expression), kita dapat mendapatkan nilai dari parameter-parameter tersebut pada lokasi-lokasi diskrit (lokasi-lokasi yang telah terdiskritisasi) di dalam domain aliran fluida dengan menggunakan CFD solver dan persamaan original dari Navier-Stokes di aproksimasi dengan menggunakan turunan aljabar. Persamaan-persamaan differential partial tersebut, secara keseluruhan di ganti dengan (replace) sebuah sistem persamaan aljabar, dan digunakan untuk menyelesaikan nilai diskrit dari variable pada medan aliran. Persamaan original differential parsial akan di diskritisasi dengan tujuan agar didapatkan nilai solusi pada titik-titik atau lokasi-lokasi yang diskrit.

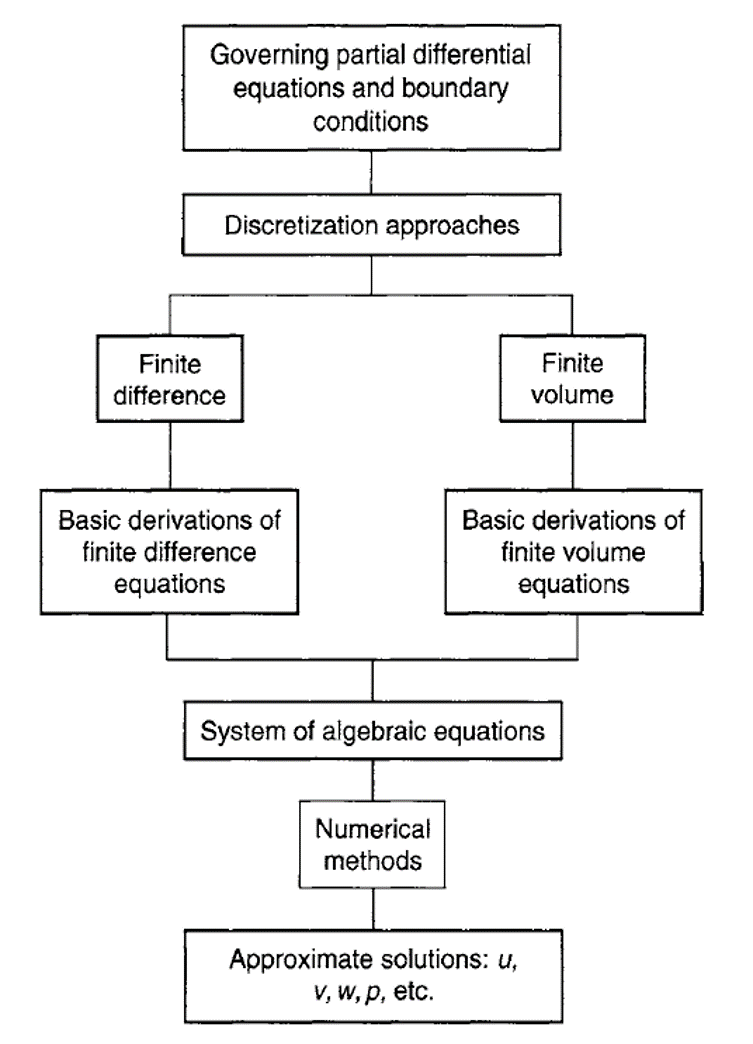
-> Pendekatan diskritisasi yang paling utama dan masih digunakan hingga saat ini adalah metode finite difference dan finite volume. Berikut proses prosedur untuk mendapatkan sebuah solusi komputasi :

-> Metode finite difference memiliki kesamaan dengan finite volume. Yang membedakan keduanya adalah dimana finite difference menggunakan fungsi polinomial yang sederhana pada elemen lokalnya untuk mendeskripsikan variasi dari variabel aliran yang tidak diketahui.

->Metode ini tidak banyak digunakan pada aplikasi CFD, walaupun telah ada program commercial dan research code nya. Hal ini karena metode diskritisasi ini membutuhkan computational resources dan daya komputasi komputer yang lebih tinggi dari pada metode finite volume.

-> Namun demikian, finite difference baik untuk dipelajari karena metode tersebut mebentuk dasar (foundation) secara comprehending(?) esensi dari dari diskritisasi(?).

-> Saat ini, CFD hampir semuanya menggunakan metode diskritisasi finite volume method. Hal ini karena kemampuannya yang dapat diaplikasikan pada structured mesh maupun unstructured mesh. Sehingga metode ini cukup populer dan dapat mengatasi kasus-kasus dengan bentuk geometri yang bermacam-macam.

a. Finite Difference Method

-> Langkah pertama dalam merepresentasikan persamaan differential parsial pada finite difference adalah dengan menggunakan ekspansi deret Taylor

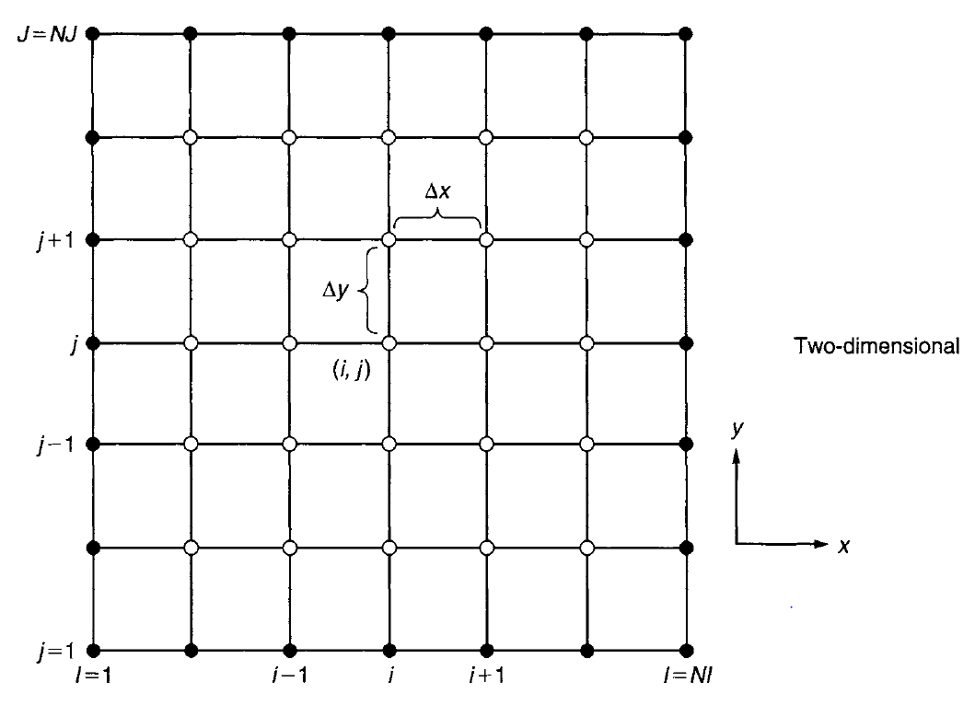Gambar 1 Nodes tertutup (hitam) menandakan nodes boundary, dan nodes terbuka (nodes transparan) menunjukkan nodes yang akan dikalkulasi secara numerik

Untuk contoh pada gambar 1, maka misalkan ada sebuah variable generic dari aliran (ɸ) pada nodes (i,j), maka dengan menggunakan deret taylor expansion pada nodes i+1 dan i-1, didapatkan sebagai berikut :

Dengan syarat bahwa nilai deret tersebut akan convergence apabila ∆X0 Dengan mengurangi kedua persamaan diatas, maka didapatkanlah persamaan sebagai berikut: