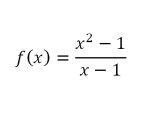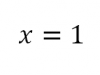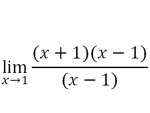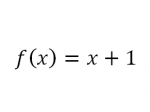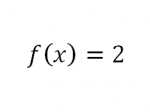Muhammad akbar
Contents
Tentang saya
Nama: Muhammad Akbar
Tempat Tanggal Lahir: Jakarta, 4 Juli 2000
Tempat Tinggal : Padang Panjang
Status: Belum menikah
Saya merupakan mahasiswa teknik perkapalan fakultas teknik universitas indonesia angkatan 2018.
sebelumnya saya belum mengerti apapun tentang metode numerik, saya tidak tahu apapun tentang pemograman dan lain sebagainya Pertemuan pertama mata kuliah metode numerik terjadi pada tanggal 7 Februari 2020. mata kuliah ini diajar oleh dua orang dosen yaitu, pak Dai dan pak harinaldi.
Pertemuan Minggu Pertama ( 7 Februari 2020 )
Pada minggu pertama mata kuliah Metode Numerik bapak Dr. Ir. Ahmad Indra Siswantara atau dikenal dengan sebutan Pak DAI memberikan pengenalan tentang metode numerik dan manfaat yang di peroleh dengan mempelajari metode numerik. Metode numerik digunakan digunakan untuk permodelan kejadian-kejadian yang ada di dunia perkapalan yang tidak bisa dilakukan secara laboraturium atau biaya melakukan percobaan yang mahal, dapat diatasi dengan menggunakan metode numerik.
Tugas Pertama Mencari Nilai Fungsi f(x)
Diketahui suatu fungsi
dimana karena jika memasukan nilai x=1 nilai yang didapat adalah 0/0 atau undefinedMaka digunakan pendekatan untuk menemukan nilai fungsi f(x) dimana x=1 dengan cara menggunakan limit
Sehingga fungsi berubah menjadi
kemudian dimasukan nilai
nilai fungsi menjadi
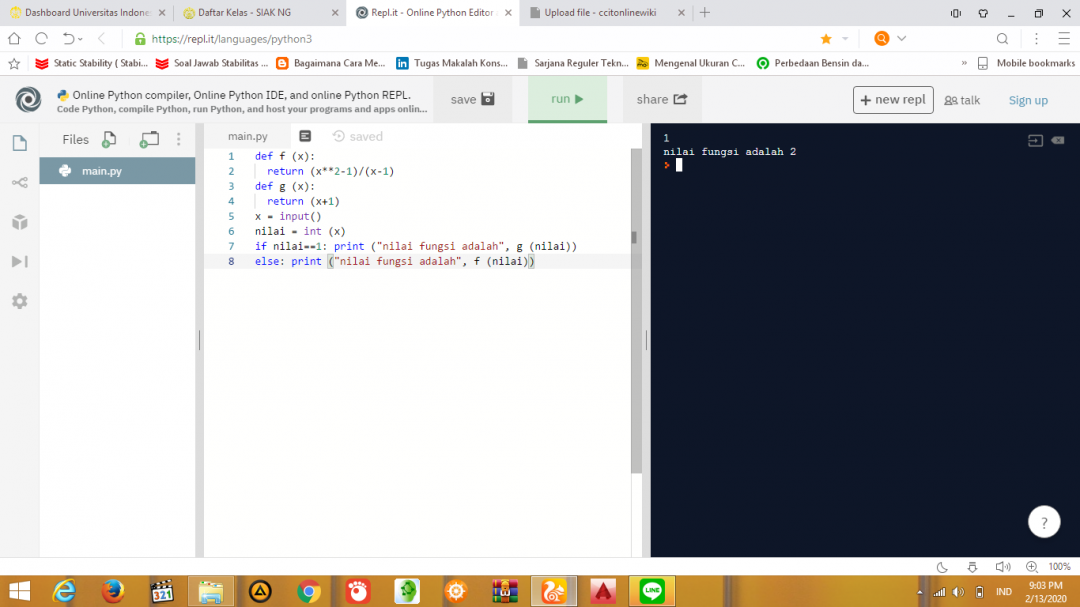
Dan jika ditulis dalam bahasa phyton menjadi
dalam bahasa bahasa phyton, kita menggunakan fungsi if, maksudnya adalah jika nilai input yang kita masukan 1 maka persamaannya akan beralih ke persamaan g, dan jika nilai x tidak sama dengan 1 maka persamaan yang berjalan adalah f.
Output
Mengerjakan tugas mencari nilai fungsi f(x) saya menjadi sedikit paham mengenai algoritma saya menjadi sedikit tertarik dengan metode numerik.
Pertemuan Minggu Kedua ( 14 Februari 2020 )
pada pertemuan minggu kedua, kami kelas metode numerik teknik perkapalan 2020 disuruh pak DAI untuk memilih soal yang menurut kami menarik. Soal yang menurut saya menarik adalah pada soal halaman 79 nomor 8.
Pada soal tersebut kita disuruh mencari masing-masing nilai x. Ada banyak cara yang dapat digunakan, yaitu dengan persamaan linear dan dengan persamaan matrix. Karena persamaan yang ada pada sooal telah disusun menjadi suatu matrix maka cara penyelesaiannya yang paling efisien adalah dengan cara matrix. Menyelesaikan persamaan matris Ax=b dimana kita disuruh untuk mencari nilai semua bilangan x maka diperlukan step agar dapat menyelesaikan persamaan tersebut. Ketika saya mempelajari aljabar linear ada banyak metode numerik yang digunakan untuk menyelesaikan permasalahan tersebut. ada metode invers dan metode Gauss-Jordan. Menggunakan metode invers, kita melakukan invers terhadap nilai A. Ax=b maka untuk mencari nilai x=A**-1 * B. dan pada saat melakukan invers juga ada banyak cara lain dilakukan untuk mencari invers suatu matrix ada metode sarrus, metode +, -, +. Sedangkan untuk metode gaus jordan kita perlu membuat persamaan matematikanya Ax=B, kemudian kita harus merubah nilai A menjadi matrix satu utama dengan metode Gauss-Jordan. dengan melakukan operasi penjumlahan dan pengurangan suatu baris dengan baris lainnya sehingga matrix yang A menjadi matrix satu utama sedangkan matrix B berubah menjadi nilai-nilai dari matrix X.
Data -> Informasi -> Pengetahuan -> Ilmu yang bermanfaat -> hikmah -> hidayah
Soal Pertama menggunakan Metode Manual
Pada metode manual saya menggunakan metode Gauss-Jordan dalam menyelesaikan permasalahan Matrix diatas. Penyelesaian permasalahan matrix menggunakan Gauss-Jordan mengharuskan kita untuk menjadikan Matrix A menjadi matrix satu utama dengan cara-cara mengoperasikan matrixnya.
Berikut saya lampirkan hasil dari pekerjaan saya menggunakan metode manual
Soal Pertama menggunakan Metode Phyton
Pada metode phyton saya menggunakan dokumen sympy yang merupakan bagian dari phyton. Di dalam dokumen sympy terdapat kumpulan program matematika. sehingga program matematika menjadi bisa dijalankan.
Berikut saya lampirkan kerjaan saya menggunakan dokumen sympy pada python. [[File:Metnum_Akbar_II_II.jpg|360px|center|alt text]