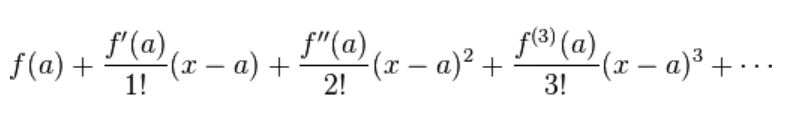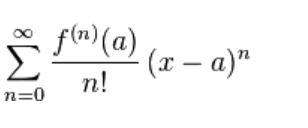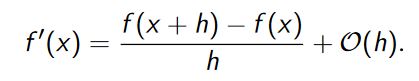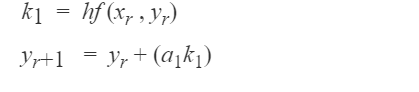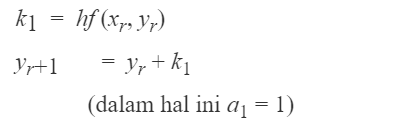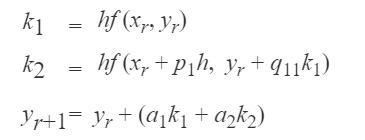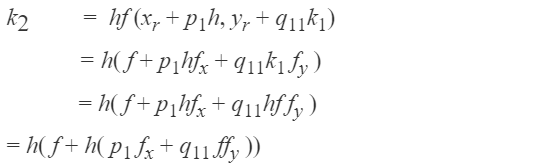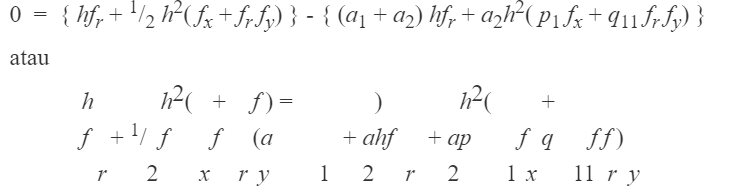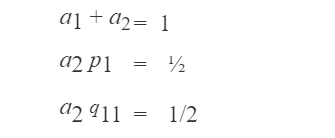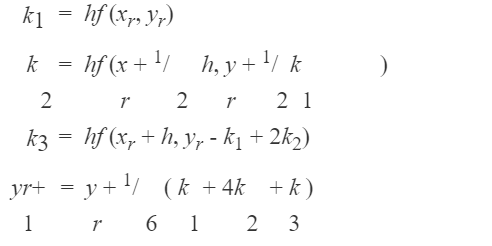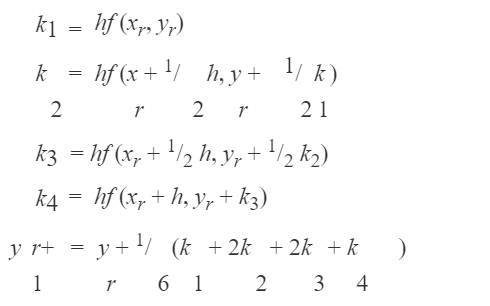Kania Gladys Clarissa Zain

Profil

Nama: Kania Gladys Clarissa Zain NPM: 1706036204 Jurusan: Teknik Mesin

Deret Taylor

Materi disampaikan oleh Bpk Dr. Ir. Engkos A. Kosasih, MT dan Bpk Dr. Ir. Ahmad Indra Siswantara

Hari dan Tanggal: 3 September 2019

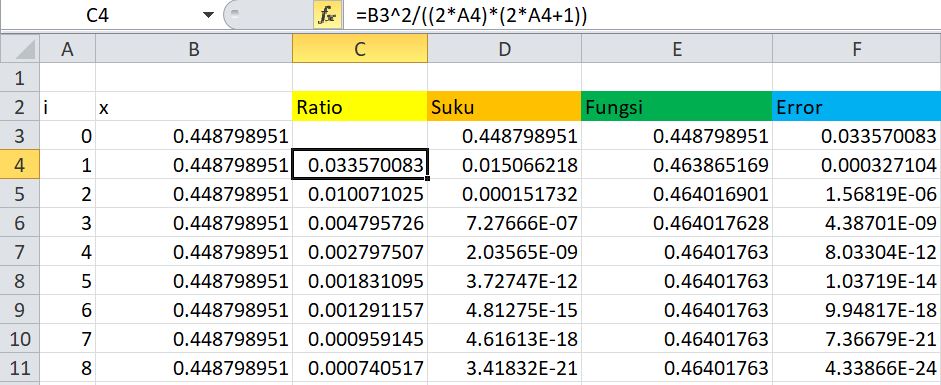
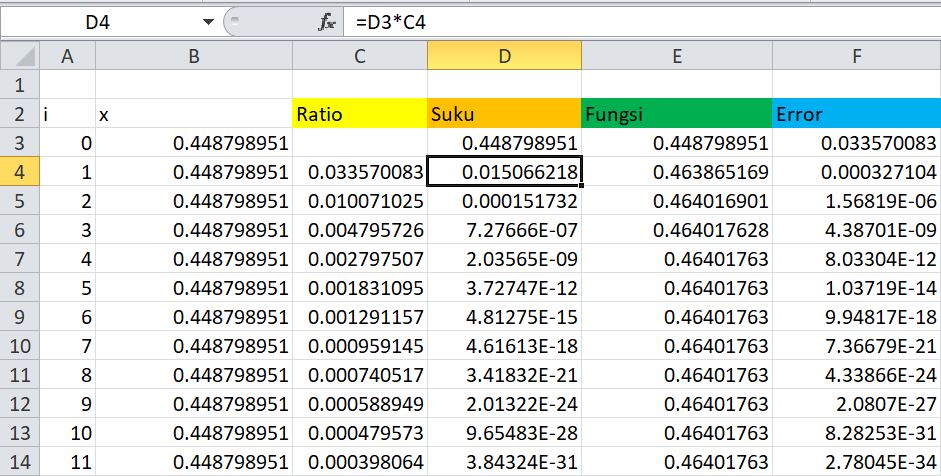
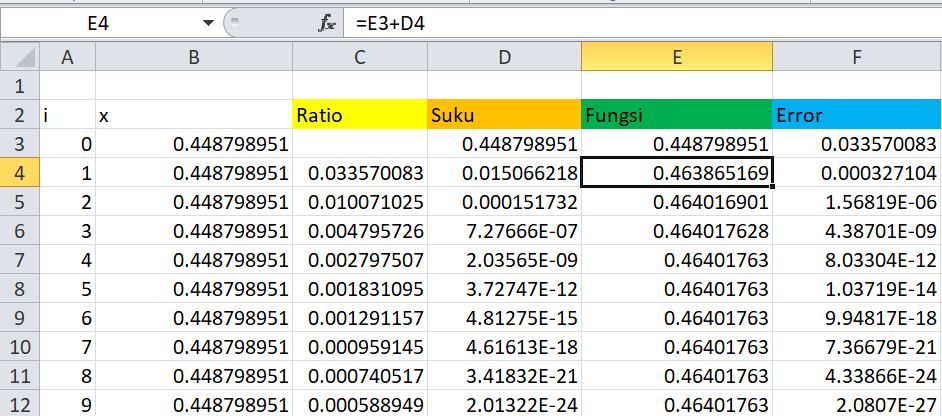
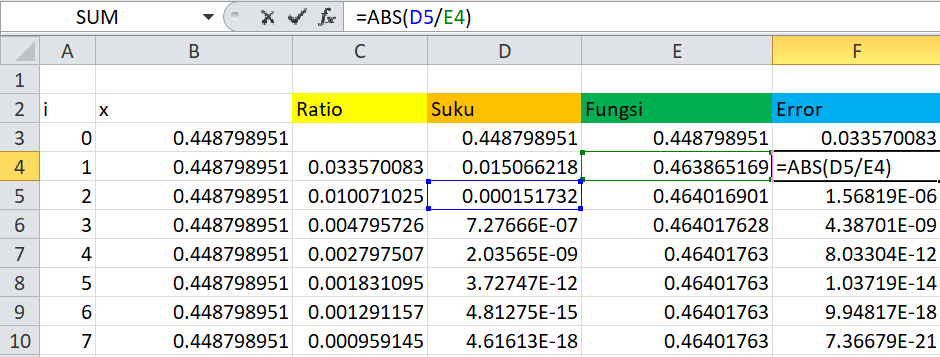
Pada hari pertama mata kuliah metode numerik, kami dijelaskan cara memformulasikan persoalan matematika sehingga dapat dipecahkan dan diolah menjadi informasi yang dapat dihitung dengan perhitungan biasa. Kami diajarkan untuk mencari rumus untuk sin pi/7 menggunakan Microsoft Excel.

Untuk mencari sinus pi/7, kami menggunakan rumus deret taylor yang berbunyi:

dan dapat disingkat menjadi:

Untuk mencari sinus pi/7, urutan yang harus dikerjakan adalah:

1. Ratio

2. Suku

3. Fungsi

4. Error

Demikian materi yang saya dapatkan di mata kuliah Metode Numerik hari pertama. Terimakasih.

Pseudocode, Tingkat Bahasa Komputer

Pada pertemuan kedua tanggal 10 September 2019, kami diajarkan mengenai pseudocode yang merupakan deskripsi dari algoritma pemrograman komputer yang menggunakan konvensi struktural dari suatu bahasa pemrograman, dan ditujukan agar dapat dibaca oleh manusia dan bukan oleh mesin.

Tujuan pseudocode adalah agar mempermudah dalam memahami bahasa pemrograman dibandingkan dengan menggunakan bahasa pemrograman yang umumnya digunakan. Keuntungan menggunakan pseudocode ini adalah waktu yang dibutuhkan relatif ringkas dan tidak bergantung pada sistem tertentu dalam suatu algoritma.

Rumus struktur pseudocode dapat dilihat sebagai berikut:

Dapat diterapkan di contoh dibawah:

Pseudocode menggunakan banyak sekali perintah-perintah, yang banyak kita pelajari, misalnya saja, IF, ELSE, THEN, serta menggunakan kode atau tanda-tanda tertentu, seperti tanda underscore (_), tanda koma, titik, tanda kutip, tanda panah kiri dan kanan, serta tanda lainnya.

Demikian materi yang saya dapatkan di mata kuliah Metode Numerik pertemuan kedua. Terimakasih.

Turunan Numerik

Pada pertemuan ketiga tanggal 17 September 2019, kami diajarkan mengenai turunan numerik. Kami diajarkan untuk menghitung hampiran dari f'(x) atau hampiran dari f(x), f'(x),....f(n)x. Selain itu kami juga di singgung tentang hampiran dari turunan parsial misalnya ∂f(x,t)/∂x.

Nilai turunan f'(x) dapat di hitung dengan:

Sedangkan nilai f(x) dan f(x-h) sendiri didapat dari teorema taylor seperti dibawah ini:

Demikian materi yang saya dapatkan di mata kuliah Metode Numerik pertemuan ketiga. Terimakasih.

Secant Method, Bisect Method, dan Newton Raphson Method

Pada pertemuan keempat tanggal 24 September 2019, kami diajarkan mengenai secant method, bisect method, dan newton raphson method.

Bisect method is the simplest numerical procedure for finding a root is to repeatedly halve theinterval[a,b], keeping the half for which f(x)changes sign.

Secant method formula can be written below:

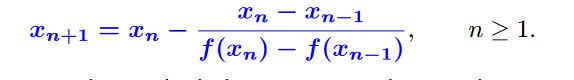
Demikian materi yang saya dapatkan di mata kuliah Metode Numerik pertemuan ke-empat. Terimakasih.

Introduction to Phyton

Pada pertemuan tanggal 29 Oktober 2019, kami diajarkan mengenai Phyton. Python adalah bahasa pemrograman tingkat tinggi yang ditafsirkan, berorientasi objek, dengan semantik dinamis. Dibangun dalam struktur data, dikombinasikan dengan pengetikan dinamis dan pengikatan dinamis, membuatnya sangat menarik untuk Pengembangan Aplikasi Cepat, serta untuk digunakan sebagai bahasa scripting atau lem untuk menghubungkan komponen yang ada bersama-sama. Seringkali, programmer jatuh cinta dengan Python karena peningkatan produktivitas yang disediakannya.

Tugas Metode Numerik

Runge Kutta

Pada pertemuan 5 November, kami diajarkan untuk menyelesaikan Engineering Problems.

Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi, dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f(x, y) pada titik terpilih dalam setiap selang langkah. Metode Runge-Kutta adalah metode Persamaan Differensial Biasa yang paling popuper karena banyak dipakai dalam praktek.

1. Metode Runge Kutta Orde-1

Galat per langkah metode R-K orde satu adalah O(h2). Galat longgokan metode R-K orde satu adalah O(h). Yang termasuk ke dalam metode Runge-Kutta orde satu ialah metode Euler:

2. Metode Runge Kutta Orde-2

Galat per langkah metode Runge-Kutta orde dua adalah O(h3). Galat longgokan metode Runge-Kutta orde dua adalah O(h2). Uraikan k2 ke dalam deret Taylor di sekitar (xr, yr) sampai suku orde satu saja:

Sedangkan k1 tidak perlu diuraikan karena sudah berada dalam bentuk (xr, yr). Dengan membuat galat per langkah Ep = 0,

Agar ruas kiri dan ruas kanannya sama, haruslah

3. Metode Runge Kutta Orde-3

Metode Runge-Kutta yang terkenal dan banyak dipakai dalam praktek adalah metode Runge-Kutta orde tiga dan metode Runge-Kutta orde empat. Kedua metode tersebut terkenal karena tingkat ketelitian solusinya tinggi (dibandingkan metode Runge-Kutta orde sebelumnya, mudah diprogram, dan stabil

Galat per langkah metode R-K orde tiga adalah O(h4). Galat longgokan metode R-K orde tiga adalah O(h3).

4. Metode Runge Kutta Orde-4

Galat per langkah metode Runge-Kutta orde empat adalah O(h3). Galat longgokan metode Runge-Kutta orde empat adalah O(h2).