Report Tugas Kelompok 4 : Metode Numerik 2019

Anggota Kelompok:

• Fikridiya Bagusrana (1706036154)
• Rifky Ramadhan Prakoso (1706036330)
• Mochamad Farhan Zidny (1706986391)
• Andika Ridwan Pratama (1706986302)

Tugas 1

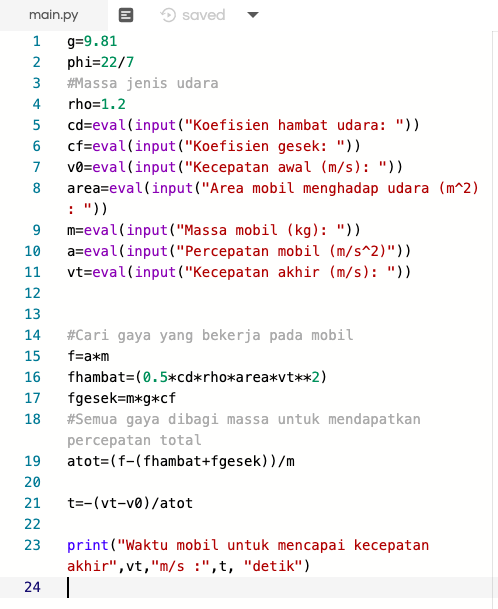
Berikut adalah governing equation pada mobil yang memiliki percepatan, gesekan, dan hambatan dengan udara.

Sebuah mobil memiliki 3 gaya yang bekerja padanya yaitu:

• F = m*a
• F gesek = m*g*cf
• F hambat = 0.5*cd*rho*area*vt^2

Dengan membagi ketiga gaya tersebut dengan massa didapatkan percepatan total

v'(t)= (F - (F gesek + F hambat))/m

Kemudian apabila disubsitusikan ke turunan dari kecepatan terhadap waktu

v'(t)= v(t)/t

dapat dicari waktu dengan cara membagi kecepatan dengan percepatan total, dimana percepatan total adalah turunan dari kecepatan terhadap waktu

t= v(t) / ((F - (F gesek + F hambat))/m)

Tugas 3

Case Description

• Airfoil memiliki karakteristik aerodinamis dan merupakan benda yang sering digunakan contohnya pada pesawat
• Thrust pada pesawat berpengaruh pada effisiensi aerodinamis, maka dari itu dibutuhkan Cl/Cd yang kecil. Cl dan Cd tergantung pada angle of attack dari airfoil.
• Airfoil yang digunakan kali ini adalah airfoil NACA 0012
• Fluida udara yang melewat air foil steady flow dan incompressible, simulasi CFD dalam kondisi adiabatic

Kemudian Airfoil yang digunakan dilakukan variasi pada 6 angle of attack yang berbeda berupa (degrees):

• 0
• 2
• 4
• 6
• 8
• 10

Simulasi CFD SOF

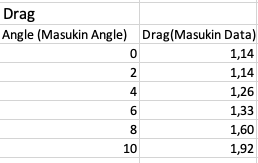
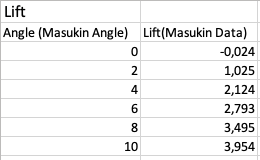
Kemudian dilakukan simulasi airfoil dan didapatkan data sebagai berikut,

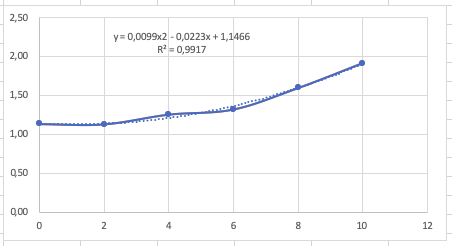
Kemudian menggunakan excel data tersebut direpresentasikan dalam bentuk grafik agar dapat melihat kurva, Grafik Drag

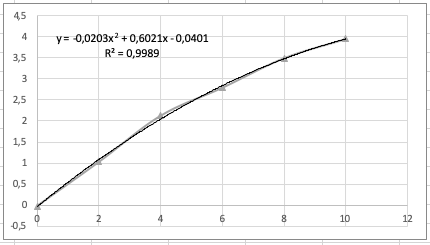
Grafik Lift

Dengan mencari rumus kurva pada excel, didapatkan rumus drag berupa y = 0,0099x2 - 0,0223x + 1,1466 dan rumus lift berupa y = -0,0203x2 + 0,6021x - 0,0401.

Optimasi

Dari kedua rumus diatas kemudian dimasukkan dalam program python dibawah ini:

import numpy as np
from scipy.optimize import minimize


def calc_drag(x):#drag
    x1 = x[0]
    drag = 0.0099*x1**2-0.0223*x1**1+1.1466
    return drag

def calc_lift(x): #lift
    x1 = x[0]
    lift = -0.0203*x1**2+0.6021*x1**1-0.0401
    return lift

def objective(x): #volume yang diminimalkan
    return calc_drag(x)

def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag
    return 90 - calc_drag(x)
def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift
    return 90 - calc_lift(x)

con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)

x1_guess = 50

x0 = np.array([x1_guess])

sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})

xopt = sol.x
forceopt = -sol.fun

dragopt = calc_drag(xopt) # drag optimal
liftopt = calc_lift(xopt) # lift optimal

print ('sudut optimal = '+str(-xopt[0]))
print ('total force optimal = '+str(forceopt))
print ('drag force optimal = '+str(-dragopt))
print ('lift force optimal = '+str(liftopt))


# In[10]:


import numpy as np
from scipy.optimize import minimize


def calc_drag(x):#drag
    x1 = x[0]
    drag = 0.0099*x1**2-0.0223*x1**1+1.1466
    return drag

def calc_lift(x): #lift
    x1 = x[0]
    lift = -0.0203*x1**2+0.6021*x1**1-0.0401
    return lift

def objective(x): #volume yang diminimalkan
    return calc_lift(x)

def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag
    return 90 - calc_drag(x)
def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift
    return 90 - calc_lift(x)

con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)

x1_guess = 50

x0 = np.array([x1_guess])

sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})

xopt = sol.x
forceopt = -sol.fun

dragopt = calc_drag(xopt) # drag optimal
liftopt = calc_lift(xopt) # lift optimal

print ('sudut optimal = '+str(xopt[0]))
print ('total force optimal = '+str(-forceopt))
print ('drag force optimal = '+str(dragopt))
print ('lift force optimal = '+str(liftopt))

Kemudian setelah program dijalan didapatkan hasil sebagai berikut:

Optimization terminated successfully.    (Exit mode 0)
            Current function value: 1.1340421717179265
            Iterations: 5
            Function evaluations: 15
            Gradient evaluations: 5
sudut optimal = -1.1262713580043062
total force optimal = -1.1340421717179265
drag force optimal = -1.1340421717179265
lift force optimal = 0.6122776950656171
Optimization terminated successfully.    (Exit mode 0)
            Current function value: -128.89494468045336
            Iterations: 7
            Function evaluations: 24
            Gradient evaluations: 7
sudut optimal = 95.86991386912578
total force optimal = -128.89494468045336
drag force optimal = 90.00000073492711
lift force optimal = -128.89494468045336