Kelompok 16
Revision as of 12:15, 4 December 2019 by Eric Delbert (talk | contribs)
Anggota Kelompok 16 :
- Eric Delbert
- Gabriella E.
- Gidion M. H.
- Sumardi
Contents
Eliminasi Gauss
Eliminasi gauss merupakan sebuah metode penyelesaian aljabar dengan memanfaatkan mmatriks sebagai variabel dalam operasi.
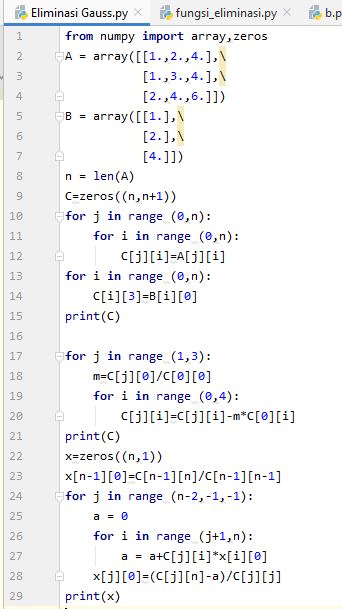
Contoh matriks
Matriks diatas dapat kita selesaikan dengan menggunakan python dengan algoritma dibawah ini
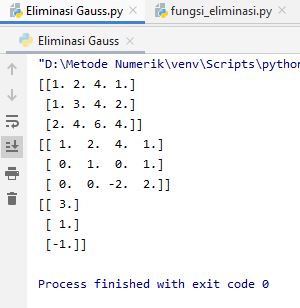
Hasil dari run file seperti ini
Untuk rincian cara muncul algoritma seperti diatas, Anda dapat lihat pada file PDF yang telah kami buat [1]
Untuk lebih lengkap inilah video tutorialnya.
Sistem Pegas
Video Teori
Video Programming
import numpy as np from numpy import array, zeros
#tentukan jumlah k
N=eval(input('jumlah k pada sistem?'))
node = N + 1
k = np.zeros((node,node), float)
# define array berisi konstanta pegas
m_k = np.zeros(N)
for i in range(0,N):
print('K',i+1,'?')
m_k[i]=eval(input())
# membangun matriks global stiffness k[0,0] = m_k[0] k[N,N]= m_k[N-1]
#pola 1
a = 0
for b in range (0,N):
a += 1
k[b,a]= -(m_k[b])
#pola 2
c = 0
for d in range (0,N):
c += 1
k[c,d]=-(m_k[d])
#pola 3
e = 0
for f in range (1,N):
e +=1
k[f,e]=m_k[f]+m_k[f-1]
print (k)
#gaya yang bekerja
Fn = eval(input('jumlah force?'))
#===============================================
J = k[1:node,1:node]
n=len(J) B=np.zeros(n,float) B[n-1]=Fn
# eliminasi gauss
for k in range (0,n-1):
for i in range (k+1, n):
if J[i,k]!=0 :
z= J[i,k]/J[k,k]
J[i,k:n]=J[i,k:n]-(J[k,k:n]*z)
B[i]=B[i]-(B[k]*z)
print(J)
u=np.zeros(n,float)
for m in range (n-1 , -1, -1):
u[m]=(B[m]-np.dot(J[m,m+1:n], u[m+1:n]))/J[m,m]
print('nilai U',m+2,u[m])
F1=-m_k[0]*u[0]
print(F1)
Persamaan diferensial dengan Runge Kutta Method
x = float(input("Masukkan nilai t untuk displacement of mass yang ingin dicari: "))
x0 = 0
y = 0
h = 0.01
if 0 <= x < 2:
def jarak(x, y):
return (2 * x**2 - 30 * y * x)
def runge_kutta(x0, y0, x, h):
n = (int)((x - x0) / h)
y = y0
for i in range(1, n + 1):
k1 = h * jarak(x0, y)
k2 = h * jarak(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * jarak(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * jarak(x0 + h, y + k3)
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Displacement of mass pada t = ", x, "s adalah", runge_kutta(x0, y, x, h), "meter"),
elif x >= 2:
def jarak(x, y):
return (8 - 30 * y * x)
def runge_kutta(x0, y0, x, h):
n = (int)((x - x0) / h)
y = y0
for i in range(1, n + 1):
k1 = h * jarak(x0, y)
k2 = h * jarak(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * jarak(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * jarak(x0 + h, y + k3)
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Displacement of mass pada t = ", x, "s adalah", runge_kutta(x0, y, x, h), "meter"),
else:
print("t yang dimasukan negatif. Silakan masukkan t secara positif.")
Algoritma diatas merupakan algoritma untuk displacement mass spring system Untuk file pptnya dapat diakses dari link ini [2]