Muhammad Fadhil Zuhdi

Profil

Nama: Muhammad Fadhil Zuhdi

NPM: 1706036186

Jurusan: Teknik Mesin

TUGAS REVIEW PELAJARAN KELAS METODE NUMERIK

• Resume 1, 3 September 2019[[1]]
• Resume 2, 10 September 2019[[2]]
• Resume 3, 17 September 2019[[3]]
• Resume 4, 24 September 2019[[4]]

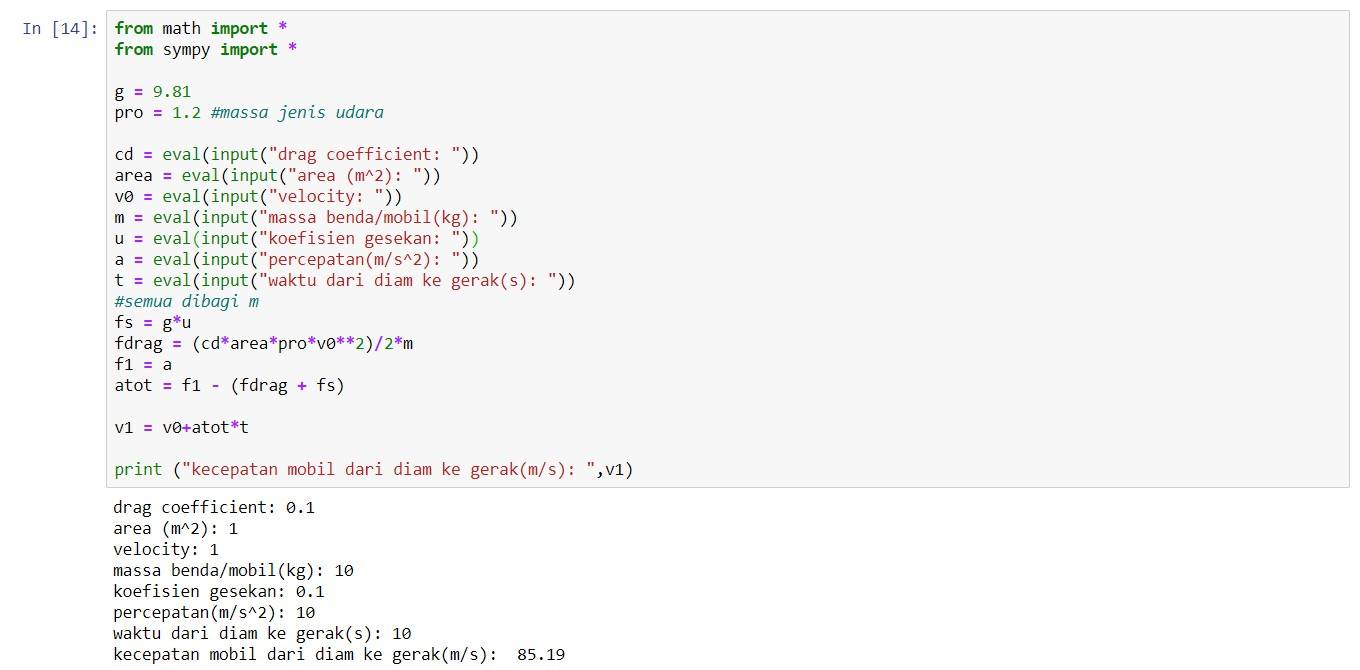
Tugas 1, 29 Oktober 2019

Mencari waktu untuk sebuah mobil mencapai kecepatan maksimal

Tugas 2, 03 November 2019

Video tutorial bagaimana cara mencari waktu sebuah untuk mencapai kecepatan maksimal oleh:

• Muhammad Fadhil Zuhdi (1706036186)
• Ilham Hutama Putra (1706036450)
• Afif Abdurrahman Ilmy (1706036280)

Hasil kerja kelompok kami: [5]

Resume Selasa, 5 November 2019

Mencari Waktu untuk Sebuah Mobil Menyentuh Kecepatan Maksimal dengan Metode Runge Kutta

Diberi sebuah studi case untuk mencari waktu sebuah mobil untuk mendapatkan kecepatan maksimal. Dari konsep awal, cara urutan berfikirnya adalah dari real life case, membuat model matematika atau numerik, dan membuat hasil analisis. Pertama kita akan mendapatkan permasalahan engineering. Dari permasalahan tersebut, model matematika atau numerik dibuat. Metode numerik dapat berupa: brainware, software, dan hardware. Kali ini, kita akan menggunakan software untuk menyelesaikan studi kasus ini. Setelah mendapatkan model matematikanya, kita menggunakan metode analisis yang ingin digunakan. Saat ini, kita akan menggunakan runge kutta method.

Runge Kutta Method Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi, dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f(x, y) pada titik terpilih dalam setiap selang langkah. Metode Runge-Kutta adalah metode PDB yang paling popuper karena banyak dipakai dalam praktek.

Bentuk umum metoda Range-Kutta orde-n ialah:

yr+1 = yr + a1k1 + a2k2 + ... + an kn

dengan a1, a2, ..., an adalah tetapan, dan

• k1 = hf (xr , yr)
• k2 = hf (xr + p1h, yr + q11k1)
• k3 = hf (xr + p2h, yr + q21k1 + q22k2)
• kn = hf (xr + pn-1h, yr + qn-1,1 k1 + qn-1,2 k2 + ... + qn-1, n-1 kn-1)

Nilai ai, pi, qij dipilih sedemikian rupa sehingga meminimumkan galat per langkah, dan persamaan (P.8.24) akan sama dengan metode deret Taylor dari orde setinggi mungkin.

• Galat per langkah metode Runge-Kutta orde-n  : O(hn+1)
• Galat longgokan metode Runge-Kutta orde-n  : O(hn)

Orde metode = n