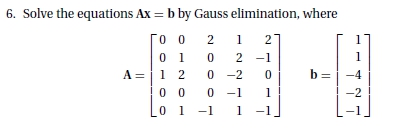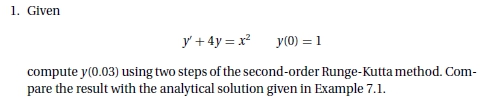Bagus Fadhlurrohman
Contents
Profil
Nama: Bagus Fadhlurrohman
NPM: 1706070633
Fakultas: Teknik
Jurusan: Teknik Mesin
BIOGRAFI
Nama saya Bagus Fadhlurrohman lahir pada tanggal 15 Juli 1999 di kota Jakarta. Saya merupakan anak pertama dari 2 bersaudara. Ayah saya seorang karyawan dan ibu saya seorang ibu rumah tangga. Saya memiliki 1 adik laki-laki yang sudah menjadi mahasiswa.
Riwayat pendidikan
2003-2005 TK Aisiyah 04 Tebet Timur
2005-2011 SDN Tebet Barat 05 Pagi
2011-2014 SMPN 115 Jakarta
2014-2017 SMAN 8 Jakarta
2017-.... S1 Teknik Mesin Universitas Indonesia
Metode Numerik
Hiburan 1
Mencari limit (x)=1 pada persamaan dengan pyhton
(x**2-1) / ((x-1)
step 1
Membuka python idle lulu mengetik program seperti berikut
def limit (x) :
try:
a = (x**2-1)
b = (x-1)
result = a / b
print (result)
except ZeroDivisionError:
c = ((x+(1/99))**2-1) / ((x+(1/99))-1)
print (c)
d = ((x+(1/999))**2-1) / ((x+(1/999))-1)
print (d)
e = ((x+(1/9999))**2-1) / ((x+(1/9999))-1)
print (e)
f = ((x+(1/99999))**2-1) / ((x+(1/99999))-1)
print (f)
g = ((x+(1/999999))**2-1) / ((x+(1/999999))-1)
print (g)
h = ((x+(1/9999999))**2-1) / ((x+(1/9999999))-1)
print (h)
print ("mendekati angka 2")
else:
print ("hasilnya", resut)
finally:
print ("sudah")
step 2
simpan program dalam bentik file.py
step 3
jalankan program pada python
step 4
nanti akan mendapatkan hasil File:Hiburan 1.jpg
Hiburan 2
Mencari nilai x pada persamaan dengan python
8x**4 + 2x**3 + x**2 - x = 0
step 1
Membuka python idle lulu mengetik program seperti berikut
def f(x):
return 8*x**3 + 2*x**2 + x - 1
def fprime(x):
return 24*x**2 + 4*x +1
ep = 0.001
gu = -10 i = 0
print('8*x**3 + 2*x**2 + x - 1')
print('Results by Python 3.7')
while abs(f(gu)) >= ep:
gu = gu - (f(gu)/fprime(gu))
i += 1
print(' ' + str(i) + ' ' + str(round(gu,7)))
print('The root approach is ' + str(round(gu,2)) +
'| failed to calculate: ' + str(i) + ' times' )
step 2
simpan program dalam bentik file.py
step 3
jalankan program pada python
step 4
nanti akan mendapatkan hasil File:Hiburan 2.jpg
Hiburan 3
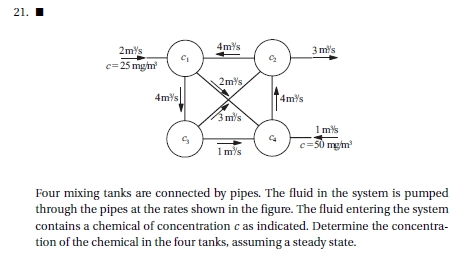
Mencari nilai setiap x pada
step 1
Tentukan persamaan pada gambar tersebut
6x1 + 4x2 = 50 2x1 + x3 + 4x4 = 50 7x2 + 3x3 + 4x4 = 50 4x1 + 4x3 = 50
Akan menghasilkan matriks
[6. -4. 0. 0.] [-4. 0. 4. 0.] [-2. 0. -1. 4.] [0. 7. -3. -4.]
step 2
tuliskan matriks di python seperti berikut
import numpy as np
A = np.array([[6, -4, 0, 0], [-4, 0 ,4, 0], [-2, 0, -1, 4], [ 0, 7, -3, -4]], float) B = np.array([50, 0, 50, 0], float)
n = len(A)
dengan eliminasi gauss
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
lalu dengan back subs
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
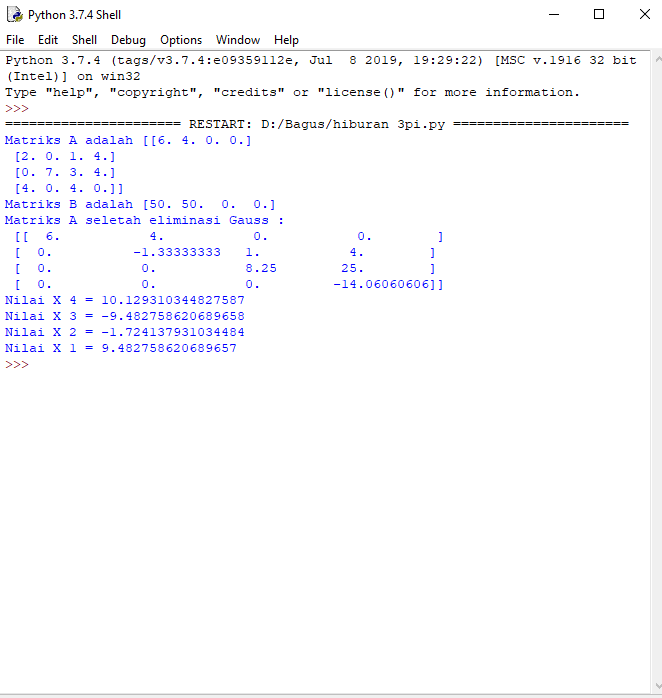
hasilnya adalah
Quiz 1
1. Mencari nilai setiap x
step 1 membuat matriks pada python
import numpy as np
A = np.array([[1, 2, 0, -2, 0], [0, 1 ,0, 2,-1], [0, 1, -1, 1, -1], [ 0, 0, 0, -1, 1], [0, 0, 2, 1, 2]], float) B = np.array([-4, 1, -1, -2, 1], float)
n = len(A)
dengan eliminasi gauss
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
lalu dengan back subs
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
hasilnya adalah
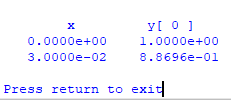
2. Mencari di y(0.03)
import numpy as np
from run_kut2 import *
from printSoln import *
from math import exp
def F(x,y):
F = np.zeros(1)
F[0] = x**2 - 4.0*y[0]
return F
x = 0.0 # Start of integration
xStop = 0.03 # End of integration
y = np.array([1.0]) # Initial values of {y}
h = 0.01 # Step size
freq = 20 # Printout frequency
X,Y = integrate(F,x,y,xStop,h)
printSoln(X,Y,freq)
input("\nPress return to exit")
UTS
no. 1
import numpy as np def GEPP(A, b):
Gaussian elimination with partial pivoting.
% input: A is an n x n nonsingular matrix
% b is an n x 1 vector
% output: x is the solution of Ax=b.
% post-condition: A and b have been modified.
n = len(A)
if b.size != n:
raise ValueError("Invalid argument: incompatible sizes between A & b.", b.size, n)
# k represents the current pivot row. Since GE traverses the matrix in the upper
# right triangle, we also use k for indicating the k-th diagonal column index.
for k in xrange(n-1):
#Choose largest pivot element below (and including) k
maxindex = abs(A[k:,k]).argmax() + k
if A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
#Swap rows
if maxindex != k:
Ak,maxindex = Amaxindex, k
bk,maxindex = bmaxindex, k
for row in xrange(k+1, n):
multiplier = A[row][k]/A[k][k]
#the only one in this column since the rest are zero
A[row][k] = multiplier
for col in xrange(k + 1, n):
A[row][col] = A[row][col] - multiplier*A[k][col]
#Equation solution column
b[row] = b[row] - multiplier*b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
print (A)
print (b)
x = np.zeros(n)
k = n-1
x[k] = b[k]/A[k,k]
while k >= 0:
x[k] = (b[k] - np.dot(A[k,k+1:],x[k+1:]))/A[k,k]
k = k-1
return x
if __name__ == "__main__":
A = np.array([[1.,0.,0.,0.],[-1.,1.,0.,0.],[0.,0.,-1.,1.],[0.,0.,0.,1.]]) b = np.array([[20.],[10.],[15.],[20.]]) print (GEPP(A,b))
no. 2
import numpy as np
# Python program to implement Runge Kutta method # Percepatan dari mobil adalah 5 m/s**2 # Gesekan udara dan mobil adalah -0.002*V m/s and -1m/s**2 # maka persamaannya menjadi v = 5*t - 1*t - 0.002*v # contoh "dv / dt = 8/1.001"
def dvdt(t,v):
return (8/1.001)
#Mencari nilai y saat x dengan step sixe h # Dengan nilai awal y0 dan x0.
def rungeKutta(t0, v0, t, h):
#count number of step size
#step h
n = (int)((t - t0)/h)
v = v0
for i in range (1, n + 1):
"menggunakan rangeKutta"
k1 = h * dvdt(t0, v)
k2 = h * dvdt(t0 + 0.5 * h, v + 0.5 * k1)
k3 = h * dvdt(t0 + 0.5 * h, v + 0.5 * k2)
k4 = h * dvdt(t0 + h, v + k3)
#next value of v
v = v + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of t
t0 = t0 + h
return v
# Driver method
t0 = 0
v = 2
t = 3
h = 0.1
print ('Nilai dari y saat s adalah:', rungeKutta(t0, v, t, h))