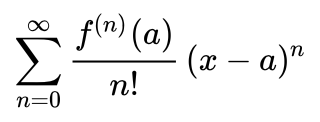Fanya Mellinda Salsabila

Profil

Nama: Fanya Mellinda Salsabila

NPM: 1706036141

Jurusan: Teknik Mesin

Pertemuan Pertama

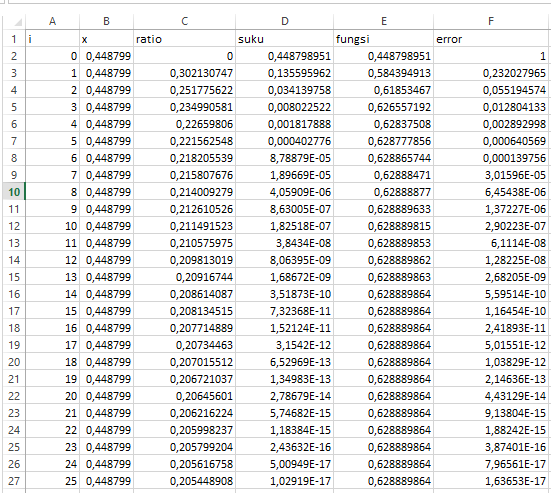
Pada pertemuan pertama mata kuliah Metode Numerik tanggal 03 September 2019, kami mempelajari cara menghitung nilai-nilai sin x, cos x, e^x, log x atau ln(x+1) menggunakan metode numerik dengan cara Deret Taylor atau Deret MacLaurin. Nilai-nilai tersebut akan rumit dihitung secara manual, maka dari itu dibutuhkan bantuan seperti kalkulator, Microsoft Excel, software programming atau tabel untuk menghitung nilai dari fungsi-fungsi tersebut. Pada pertemuan kali ini, kami diberi latihan menggunakan Microsoft Excel dengan langkah-langkah sebagai berikut:

Dengan:

i = 0-25

x = pi/7

Rumus-rumus:

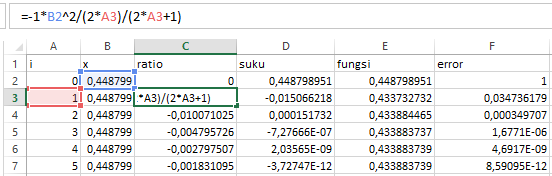
1. Ratio

Ratio merupakan penyerdehanaan dari rumus deret taylor sebagai berikut:

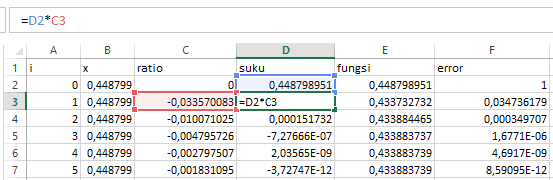
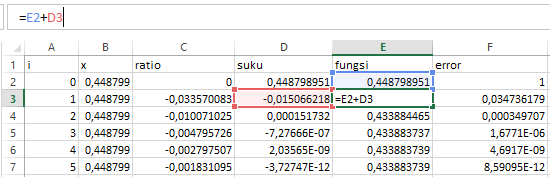
2. Suku

3. Fungsi

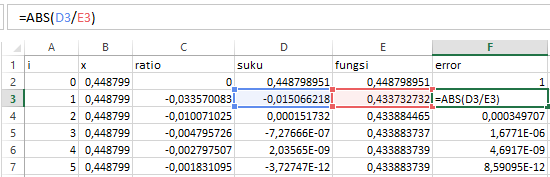
4. Error

Pertemuan Kedua

Pseudocode

Pseudocode adalah deskripsi tingkat tinggi informal dan ringkas atas algoritma pemrograman komputer yang menggunakan konvensi struktural atas suatu bahasa pemrograman, dan ditujukan untuk dibacaoleh manusia dan bukan oleh mesin. Pseudocode merupakan kode yang mirip dengan pemograman sebenarnya.

Pseudocode berasal dari kata Pseudo yang berarti imitasi, mirip, atau menyerupaidengan kode bahasa pemograman. Dalam penulisan pseudocode tidak ada aturan yang baku, oleh karena itu pseudocode biasanya ditulis berbasiskan bahasa pemograman yang akan digunakan, misalnya Basic, pascal, C++ dan lain-lain. Sehingga lebih tepat digunakan untukmenggambarkan algoritma yang akan dikomunikasikan kepada programmer.

Pada hari Selasa, 10 September 2019 kami diberikan latihan untuk mencari nilai dari sin x, cos x, dan e^x sebagai berikut:

Pertemuan Ketiga

Turunan Numerik

Metode numerik digunakan untuk menyelesaikan persamaan-persamaan diferensial (dan juga integral) yang kompkleks. Suatu persamaan diferensial biasa orde satu atau lebih akan diselesaikan menggunakan pendekatan metode numerik yang diturunkan dari deret Taylor dan metode beda hingga (finite difference).

Cara numeris untuk menyelesaikan problem nilai awal adalah diferensial hingga. Pada metode diferensial hingga, penyelesaian pendekatan didapat pada titik- titik hitung

dan nilai pendekatan pada setiap xi diperoleh dengan menggunakan nilai yang telah diperoleh sebelumnya.