User:Umarfa

Tugas Komputasi Teknik Ke-1

DAI5

Kerangka kerja penulisan DAI5 adalah pendekatan terstruktur yang membantu penulis membuat tulisan yang jelas dan persuasif, terutama berguna untuk presentasi, proposal, dan argumen terstruktur lainnya. Kerangka kerja DAI5 terbagi menjadi lima komponen utama:

1. Data: Ini adalah fondasi faktual dari tulisan Anda. Data mencakup statistik, temuan penelitian, atau bukti apa pun yang mendukung pesan inti. Dengan mendasarkan tulisan Anda pada data yang kuat, Anda meningkatkan kredibilitas dan memberikan dasar konkret untuk argumen Anda.

2. Analisis: Di sini, Anda menafsirkan data yang disajikan. Analisis menjelaskan apa arti data tersebut, mengapa data tersebut penting, dan bagaimana data tersebut berhubungan dengan topik atau masalah Anda. Bagian ini membangun jembatan antara informasi mentah dan wawasan, membantu pembaca melihat relevansi data.

3. Wawasan (Insight): Wawasan adalah kesimpulan unik atau hasil dari analisis Anda. Wawasan menjawab pertanyaan “Lalu apa?”, menjelaskan implikasi dari data dan analisis. Wawasan harus jelas dan mudah diingat, memberikan alasan kepada pembaca untuk peduli dengan pesan tersebut.

4. Implikasi: Bagian ini mengkaji konsekuensi atau hasil potensial berdasarkan wawasan yang diberikan. Hal ini dapat mencakup dampak positif dan negatif, tren masa depan, atau tantangan yang diantisipasi. Implikasi membuat tulisan Anda berwawasan ke depan dan membantu pembaca mengantisipasi apa yang akan terjadi selanjutnya.

5. Implementasi: Pada langkah terakhir ini, Anda menyarankan langkah-langkah atau solusi yang dapat ditindaklanjuti. Implementasi memberikan pembaca jalan yang jelas ke depan, sehingga memudahkan mereka untuk menerapkan ide-ide atau mengambil tindakan berdasarkan wawasan Anda.

Kerangka kerja DAI5 dirancang untuk membuat topik yang kompleks menjadi lebih mudah dipahami, persuasif, dan dapat ditindaklanjuti, memandu pembaca dari data ke tindakan yang bermakna.

---

Question: To derive finite element equations from 1D partial differential equations (PDEs) using the weighted residual method, let's follow a straightforward example. We'll take a 1D Poisson equation as the governing equation and go through the process step by step.

Question: Can you provide with algorithm, flow chart and python code

2. Algorithm

3. Python Code

   import numpy as np
   import matplotlib.pyplot as plt
   
   # Problem setup
   L = 1.0           # Length of the domain
   N = 10            # Number of elements
   u0, uL = 0, 0     # Dirichlet boundary conditions at x=0 and x=L
   f = lambda x: 1   # Source term f(x), assumed to be constant here
   
   # Discretize the domain
   nodes = np.linspace(0, L, N+1)     # N+1 nodes
   h = L / N                           # Element length
   
   # Initialize global stiffness matrix K and load vector F
   K = np.zeros((N+1, N+1))
   F = np.zeros(N+1)
   
   # Element stiffness matrix and load vector (for linear elements)
   Ke = (1/h) * np.array([[1, -1], [-1, 1]])
   Fe = lambda x1, x2: (h / 2) * np.array([f(x1), f(x2)])
   
   # Assemble the global matrix and vector
   for i in range(N):
       x1, x2 = nodes[i], nodes[i+1]  # Nodes of the current element
       F_e = Fe(x1, x2)               # Element load vector
       K[i:i+2, i:i+2] += Ke          # Add element stiffness to global matrix
       F[i:i+2] += F_e                # Add element load to global vector
   
   # Apply Dirichlet boundary conditions
   K[0, :] = 0
   K[0, 0] = 1
   F[0] = u0
   
   K[N, :] = 0
   K[N, N] = 1
   F[N] = uL
   
   # Solve the linear system
   U = np.linalg.solve(K, F)
   
   # Plot the solution
   plt.plot(nodes, U, '-o', label="FEM Solution")
   plt.xlabel("x")
   plt.ylabel("u(x)")
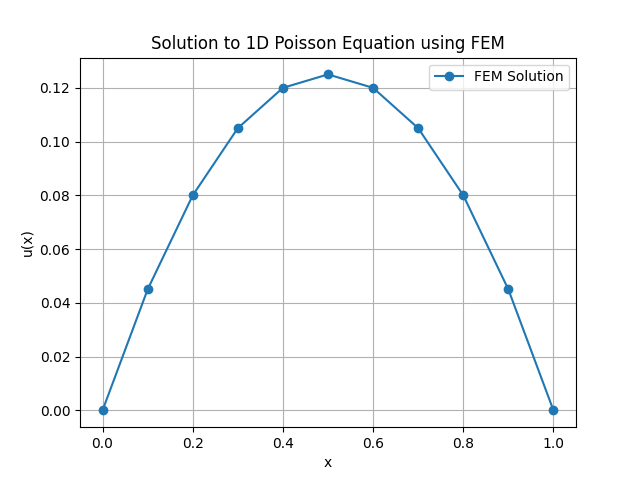
   plt.title("Solution to 1D Poisson Equation using FEM")
   plt.legend()
   plt.grid(True)
   plt.show()

Sehingga menghasilkan gradfik sebagai berikut:

Tugas Komputasi Teknik Ke-2

Pada pertemuan sebelumnya, kami akan melakukan diskusi dengan Chatgpt sebagai berikut:

Question: In the context of mechanical engineering, please explain the difference of grad student, master degree student, and doctoral student, please explain in pointers and make a summary of the difference in table format.

Answer: Here’s a detailed comparison of graduate students, master’s degree students, and doctoral students in the context of mechanical engineering:

---

Differences in Graduate Programs and Students:

Graduate Student:

- Definition: Refers to any student pursuing post-bachelor's level education.
- Program Type: Encompasses both master's and doctoral programs.
- Scope: Can pursue either a Master’s or PhD in mechanical engineering, depending on the academic or career goals.
- Duration: Typically varies from 1-7+ years depending on the degree (master’s vs. doctoral).
- Goal: Gain specialized knowledge and technical skills in a field of study.

Master's Degree Student:

- Definition: A student pursuing a Master’s degree (M.Sc., M.Eng., or M.S.) in mechanical engineering.
- Program Type: Non-terminal or terminal; can lead to PhD studies or serve as the highest degree attained.
- Scope: Focus on advanced knowledge, with options for coursework-only or thesis research-based programs.
- Duration**: Generally 1-2 years, depending on full-time or part-time status and program structure.
- Goal: Deepen understanding in a specific area of mechanical engineering or prepare for industry roles.
  

Doctoral (PhD) Student:

- Definition: A student working toward a Doctor of Philosophy (PhD) in mechanical engineering.
- Program Type: Research-intensive, focused on generating new knowledge through original research.
- Scope: Involves extensive research, dissertation writing, and potential teaching responsibilities.
- Duration: Typically 3-7+ years, highly dependent on research progress.
- Goal: Prepare for academic, research, or advanced industry positions requiring original research skills and high specialization.

---

Dalam framework Dynamic Awareness and Intentionality (DAI5), konsep Conscious Continuum adalah salah satu aspek penting yang digunakan untuk mengukur tingkat kesadaran (consciousness) dan kemampuan responsif dalam sistem berbasis kecerdasan buatan (AI). Conscious Continuum mengacu pada spektrum tingkat kesadaran, dari respons reaktif yang sederhana hingga pemahaman dan respons yang kompleks berdasarkan konteks yang lebih mendalam.

Berikut adalah penjelasan mengenai tingkat kesadaran dalam Conscious Continuum pada DAI5:

1. Reactive Awareness (Kesadaran Reaktif): Pada level ini, AI hanya merespons rangsangan atau perintah sederhana tanpa pemahaman kontekstual. Sistem hanya mampu memberikan respons otomatis yang tidak mempertimbangkan informasi tambahan di luar input dasar.

2. Situational Awareness (Kesadaran Situasional): Di level ini, AI mampu mengenali dan mempertimbangkan konteks dasar dalam lingkungannya. Sistem memiliki kesadaran terbatas yang memungkinkan pemahaman lebih mendalam, seperti memperhatikan data lingkungan untuk menyesuaikan respons, namun belum sampai pada pengambilan keputusan yang kompleks.

3. Contextual Awareness (Kesadaran Kontekstual): Pada tahap ini, AI mulai memahami konteks yang lebih luas dari situasi atau permintaan yang diterima. Sistem mempertimbangkan faktor-faktor yang lebih kompleks dan memperhitungkan hubungan antar faktor untuk menghasilkan respons yang lebih akurat dan relevan.

4. Intentional Awareness (Kesadaran Intensional): Di sini, AI dapat mengidentifikasi maksud di balik suatu permintaan atau situasi dan menyesuaikan respons sesuai dengan tujuan yang lebih spesifik. Sistem mampu mengidentifikasi tujuan pengguna atau situasi yang dihadapi sehingga dapat memberikan respons yang lebih tepat sasaran.

5. Self-Aware Consciousness (Kesadaran Diri): Pada level tertinggi, AI tidak hanya memahami lingkungan atau tujuan, tetapi juga memiliki pemahaman tentang dirinya sendiri dalam proses pengambilan keputusan. Sistem AI dengan kesadaran diri ini dapat menilai responsnya sendiri dan mempertimbangkan implikasi lebih dalam dari tindakannya.

Conscious Continuum ini bertujuan untuk menggambarkan kemajuan level kesadaran yang dimiliki AI dalam memahami dan merespons konteks, sehingga memungkinkan AI untuk bekerja dengan lebih efektif dalam situasi yang membutuhkan respons yang adaptif dan kontekstual.

Dalam konteks mekanika kontinuum, kita melihat material sebagai benda yang "kontinu" — artinya, material dianggap memiliki sifat yang sama di seluruh bagiannya dan tidak terdapat rongga atau partikel diskret di dalamnya. Pendekatan ini sangat penting dalam rekayasa karena memudahkan analisis perilaku material ketika dikenai beban atau tekanan.

---

Contoh Praktis pada Mekanika Kontinuum dengan Analogi Kesadaran (Conscious Continuum) DAI5

Mari kita ambil contoh sederhana dalam mekanika kontinuum, yaitu analisis deformasi batang 1D ketika dikenakan gaya tarik. Dalam contoh ini, kita akan menggunakan pendekatan "kesadaran kontinu" (Conscious Continuum) dari *DAI5 Framework* karya Dr. Ahmad Indra, yang terdiri dari:

1. Initiator (Inisiator) : Merupakan faktor atau pemicu awal yang menyebabkan terjadinya respons di dalam material atau sistem. Dalam hal ini, gaya tarik yang diberikan pada batang berperan sebagai inisiator. Ketika gaya diterapkan, batang merespons dengan deformasi atau perubahan bentuk sesuai dengan materialnya.

2. Intention (Niat) : Ini adalah maksud atau tujuan dari respons yang diinginkan oleh material. Untuk kasus batang 1D ini, niatnya adalah mempertahankan kestabilan bentuk atau mengakomodasi perubahan yang dihasilkan dari gaya tarik tersebut. Batang "secara intensional" menyesuaikan dirinya untuk mencapai keseimbangan baru saat gaya diberikan.

3. Initial Thinking (Pemikiran Awal) : Pada tahap ini, kita menganggap bagaimana batang akan merespons gaya yang diberikan, misalnya melalui pemahaman dasar sifat elastisitas atau modulus Young dari material tersebut. Dalam mekanika kontinuum, pendekatan ini mengasumsikan bahwa respons batang terhadap gaya akan konsisten di seluruh panjangnya.

4. Idealization (Idealisasi) : Mekanika kontinuum mengidealisasi batang ini sebagai material yang homogen dan isotropik (sifatnya sama di seluruh arah). Pada tahap ini, kita menghitung deformasi menggunakan hukum Hooke dan menganggap material kontinu sehingga seluruh batang berperilaku seragam terhadap gaya yang diberikan. Dalam bahasa persamaan, kita bisa menghitung deformasi (ΔL) sebagai:

5. Instruction Set (Set Instruksi) : Merupakan serangkaian langkah atau aturan yang diterapkan pada batang berdasarkan hasil idealisasi. Dalam hal ini, instruksi setnya adalah menggunakan persamaan hukum Hooke untuk menghitung deformasi yang dialami batang. Setelah menghitung, kita dapat menafsirkan hasil deformasi tersebut sebagai respons kontinu dari material yang mempertahankan konsistensi dalam karakteristiknya (seperti modulus Young yang konstan).

Jadi, batang baja akan mengalami deformasi sebesar 0.952 mm ketika dikenai gaya tarik 1000 N. Hasil ini menunjukkan respons kontinu batang terhadap gaya yang diterapkan berdasarkan pendekatan mekanika kontinuum.

Integrasi *Conscious Continuum* dalam Framework DAI5

Dengan menyelaraskan pendekatan mekanika kontinuum dalam "kesadaran kontinu" framework DAI5, kita bisa melihat bagaimana pendekatan ini secara bertahap mengukur respons material secara bertahap, dari gaya awal (initiator), melalui niat responsif, hingga idealisasi yang memungkinkan kita untuk memahami respons kontinu pada level instruksi set. Dalam pendekatan DAI5, ini menciptakan respons yang "disadari" dalam interpretasi rekayasa material, yang secara efektif memberikan solusi dan prediksi yang sesuai untuk aplikasi dalam rekayasa.