User:Muhammad Abyan Arkan

Nama : Muhammad Abyan Arkan NPM  : 2106637201

PROGRES PEKAN 1

kapasitas 1 liter
       pressure 8 bar
       biaya produksi maks. Rp. 500.000

1. Pemilihan Tangki: Cari bahan tangki yang ringan dan hemat biaya yang dapat menahan tekanan yang diinginkan. Pilihan umum termasuk komposit serat karbon atau baja berkekuatan tinggi. Bandingkan biayanya dan pilih opsi yang paling sesuai dengan anggaran Anda.

2. Desain Tangki: Optimalkan desain tangki untuk meminimalkan penggunaan material sambil memastikan integritas struktural. Pertimbangkan faktor-faktor seperti bentuk tangki, ketebalan dinding, dan teknik penguatan untuk mencapai nilai volume dan tekanan yang diinginkan.

3. Tindakan Keselamatan: Terapkan fitur keselamatan yang sesuai untuk mencegah kebocoran atau pecahnya tangki. Ini mungkin termasuk katup pelepas tekanan, burst disk, dan sensor tekanan untuk memantau integritas tangki.

4. Pemilihan Katup: Pilih katup yang cocok untuk mengisi dan mengeluarkan gas hidrogen. Cari opsi hemat biaya yang dapat menangani peringkat tekanan yang diinginkan.

5. Bahan Penyegelan dan Gasket: Pilih bahan penyegelan dan gasket berkualitas tinggi yang kompatibel dengan gas hidrogen dan dapat memberikan segel yang andal untuk mencegah kebocoran.

6. Integrasi Sistem: Pastikan integrasi yang tepat dari sistem penyimpanan dengan pembangkitan hidrogen atau sistem suplai. Pertimbangkan kompatibilitas titik sambungan, fiting, dan selang untuk menghindari kebocoran atau penurunan tekanan.

7. Pengoptimalan Biaya: Untuk mengoptimalkan biaya, pertimbangkan untuk mencari bahan dan komponen dari pemasok yang andal dan hemat biaya. Selain itu, jelajahi kemungkinan menggunakan komponen standar atau solusi siap pakai untuk mengurangi biaya pembuatan dan kustomisasi.

8. Pengujian dan Sertifikasi: Lakukan pengujian menyeluruh dan dapatkan sertifikasi yang diperlukan untuk memastikan sistem penyimpanan memenuhi standar keselamatan dan persyaratan kinerja. Langkah ini sangat penting untuk menghindari potensi bahaya dan mendapatkan kepercayaan dari pengguna akhir.

Penting untuk diperhatikan bahwa biaya sistem penyimpanan hidrogen dapat sangat bervariasi tergantung pada beberapa faktor, seperti bahan yang dipilih, teknik produksi, dan kondisi pasar. Oleh karena itu, mungkin perlu berkonsultasi dengan pakar, insinyur, atau produsen penyimpanan hidrogen untuk mendapatkan perkiraan biaya yang lebih akurat dan rekomendasi desain khusus.

PROGRES PEKAN 2

Dibawah ini disajikan kode Python yang dapat digunakan untuk mengoptimalkan penyimpanan hidrogen pada tekanan 8 bar dengan kapasitas 1 liter dan anggaran maksimal Rp500.000:

from scipy.optimize import minimize

# Harga dan kapasitas yang dibutuhkan
harga_per_unit = 500000  # Rupiah
kapasitas_per_unit = 1  # Liter

# Anggaran maksimal
anggaran_maksimal = 500000

# Fungsi Akhir
def fungsi_akhir(x):
    return -x * kapasitas_per_unit

# Kendala yang terjadi
def kendala(anggaran):
    return anggaran_maksimal - (harga_per_unit * anggaran)

kendala_anggaran = {'type': 'ineq', 'fun': kendala}

# Nilai awal
x0 = 0

# Batasan
batas = [(0, None)]

# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_akhir, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])

# Menampilkan hasil
print("Status:", solusi.success and "Biaya Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit yang bisa dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan yang didapat:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total anggaran:", solusi.x[0] * harga_per_unit, "Rupiah")

Output:

Status: Biaya Optimal
Jumlah unit yang bisa dibeli: 1
Total kapasitas penyimpanan yang didapat: 1.0 liter
Total anggaran: 500000.0 Rupiah

Kode di atas memiliki tujuan utama untuk memaksimalkan jumlah unit penyimpanan hidrogen yang akan dibeli. Batasan anggaran diimplementasikan menggunakan fungsi kendala untuk memastikan bahwa total biaya tidak melebihi anggaran maksimal yang telah ditentukan dan Output dari kode ini akan menampilkan jumlah unit yang perlu dibeli, total kapasitas penyimpanan, dan total biaya yang diperlukan.

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# Harga dan kapasitas
harga_per_unit = 500000  # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1  # Kapasitas penyimpanan hidrogen per unit

# Anggaran maksimal
budget_maksimal = 500000

# Fungsi tujuan
def fungsi_tujuan(x):
    return -x

# Kendala
def kendala(x):
    return budget_maksimal - (harga_per_unit * x[0])

kendala_anggaran = [{'type': 'ineq', 'fun': kendala}]

# Nilai awal
x0 = [0]

# Batasan
batas = [(0, None)]

# Membuat fungsi untuk menampilkan hasil
def tampilkan_hasil(solusi):
    print("Status:", "Optimal" if solusi.success else "Tidak ditemukan solusi")
    print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
    print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
    print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")

# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=kendala_anggaran)

# Menampilkan hasil
tampilkan_hasil(solusi)

# Menghasilkan grafik
anggaran = np.linspace(0, 10, 100)  # Range anggaran
kapasitas = anggaran * kapasitas_per_unit  # Total kapasitas penyimpanan untuk setiap anggaran
biaya = anggaran * harga_per_unit  # Total biaya untuk setiap anggaran

plt.figure()
plt.plot(anggaran, kapasitas, label='Kapasitas Penyimpanan')
plt.plot(anggaran, biaya, label='Total Biaya')
plt.axhline(solusi.x[0] * kapasitas_per_unit, color='b', linestyle='--', label='Jumlah Unit Optimal')
plt.axvline(solusi.x[0], color='y', linestyle='--', label='Anggaran Optimal')
plt.xlabel('Anggaran')
plt.ylabel('Kapasitas/Biaya')
plt.title('Optimisasi Penyimpanan Hidrogen')
plt.legend()
plt.grid(True)
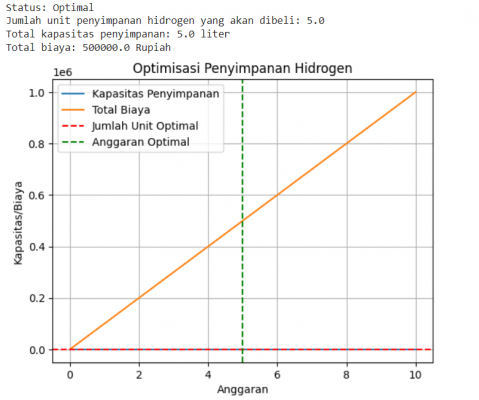
plt.show()

Kode di atas berfungsi untuk menghitung jumlah optimal unit penyimpanan hidrogen yang akan dibeli berdasarkan harga per unit, kapasitas per unit, dan anggaran maksimal yang diberikan. Kode ini memberikan solusi terbaik dengan kapasitas total tertinggi yang tetap berada dalam anggaran. Hasilnya kemudian dicetak, termasuk jumlah unit, kapasitas total, dan biaya total. Selain itu, kode ini juga membuat grafik yang menunjukkan hubungan antara kapasitan dan anggaran optimisasi penyimpanan hidrogen