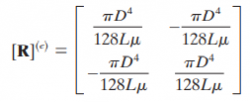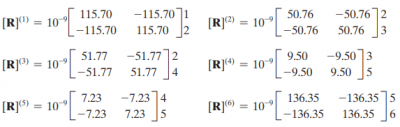Mekanika Fluida - Josiah Enrico S (1906356286)
Contents
Title: Modelica-based Simulation of Viscous Flow Through Pipes Using Finite Element Formulation
Abstract
As the piping system has always become an integral part of any fluid-related mechanical system, controlling and measuring the flow properties, such as pressure, flow rate and Reynolds number inside the pipe is a necessary field to master in order to engineer the efficient arrangement. These properties are critical and can be analytically computed by considering fluid factors like density or viscosity and the pipe dimension. Unfortunately, this current method is not scalable since it is examined too onerous and time-consuming to address complex systems. On the other hand, many numerical method programming has been developed to help engineers overcome those problems. This white paper will recreate one simple problem of a multiple pipes system utilizing Modelica programming language and compare it with the current analytical technique to verify the results. This simulation is expected to be a base in developing a scalable program for multiple pipe systems in further work.
Introduction
Objectives
The objectives of this study are as follows:
- Develop a Modelica-based simulation to compute the pressure, flow rate, and Reynolds numbers in the selected points.
- Validate the results with the corresponding resources.
- Verify the results with the parameters and boundaries.
Methodology
- The Analytical Calculation
- Based on the formula analysis above, we can first determine the local elemental flow resistance in each of 6 points. The matrix can be written as
- And the local matrix of the 6 points are:
- The Simulation Program
- This program is separated into two sections, the first one is the definition phase where the operator needs to input all the properties and the pipe geometry at once. There are 2 fluid properties considered which are dynamic viscosity (N∙s/m2)to calculate the head loss and the density (kg/m3) to calculate the Reynolds number. To set the limit point and boundary condition, the measured pressure (Pa) at the inlet and outlet are also defined at point 1 and 6. Afterward, the parameter of piping like its diameter and installed distance are collected using 2 column matrix. The additional data of Q inlet or point 1 is used to verify the result at the end of the simulation.
- The second section is the algorithm section where those data are processed into the requested solution. This step will include the steps mentioned in the analytical calculation above starting from making the local 4x4 matrix of elemental flow resistance, combining them to one global 6x6 matrix, applying boundary conditions, and finally computing the pressure at 6 points also flow rate and Reynolds number at 6 connected pipes.
- The program flowchart is as follows:
model Tugas_Besar_Mekflu
// ==================================== DEFINITION PHASE ====================================
parameter Real miu = 0.3 "dynamic viscosity";
parameter Real rho = 900 "density";
parameter Real Qinlet = 5e-4 "flow rate inlet";
parameter Real Pinlet = 39182 "pressure inlet";
parameter Real Poutlet = -3665 "pressure inlet";
parameter Integer boundary[:] = {1, 6} "Boundary Point";
parameter Integer nPipe = 6 "number of piping";
parameter Integer nPoint = 6 "number of point connected";
final constant Real pi=2*Modelica.Math.asin(1.0);
//Inputing pipe connection, length (L) and diameter (D)
parameter Real data[nPipe,2] = [ 70.71, 0.1 ;
50.99, 0.075 ;
50 , 0.075 ;
53.85, 0.05 ;
70.71, 0.05 ;
60 , 0.1 ];
parameter Integer no[nPoint,2] = [ 1, 2;
2, 3;
2, 4;
3, 5;
4, 5;
5, 6];
//Solution
Real Pressure[nPoint], Flowrate[nPipe], Reynolds[nPipe];
protected
Real g[nPoint,nPoint], G[nPoint,nPoint], id[nPoint,nPoint]=identity(nPoint), P[nPoint], Res;
// ==================================== SOLUTION PHASE ====================================
algorithm
//Iterating to create global matrice
for i in 1:nPipe loop
Res:= pi*data[i,2]^4/(128*data[i,1]*miu);
g:=zeros(nPoint,nPoint);
g[no[i,1],no[i,1]]:= Res;
g[no[i,1],no[i,2]]:= -Res;
g[no[i,2],no[i,1]]:= -Res;
g[no[i,2],no[i,2]]:= Res;
G:= G+g;
end for;
//Implementing boundary
for i in boundary loop
for j in 1:nPoint loop
G[i,j]:= id[i,j];
end for;
end for;
//Solving pressure in each point connected
P[boundary[1]]:= Pinlet;
P[boundary[2]]:= Poutlet;
Pressure:= Modelica.Math.Matrices.solve(G,P);
//Solving flowrate in each pipe
for i in 1:nPipe loop
Flowrate[i]:= pi*data[i,2]^4/(128*data[i,1]*miu)*(Pressure[no[i,1]]-Pressure[no[i,2]]);
end for;
//Solving Reynolds Number in each pipe flow
for i in 1:nPipe loop
Reynolds[i]:= 4*rho*Flowrate[i]/(pi*miu*data[i,2]);
end for;
end Tugas_Besar_Mekflu;
|