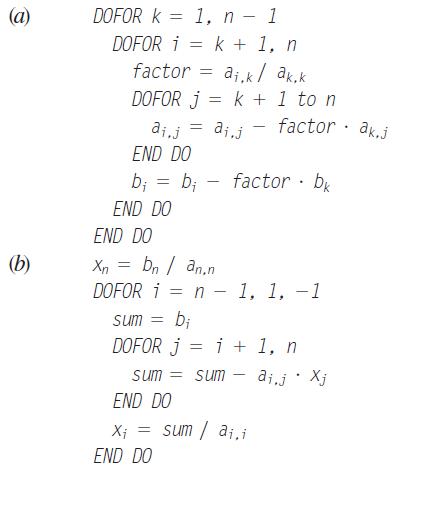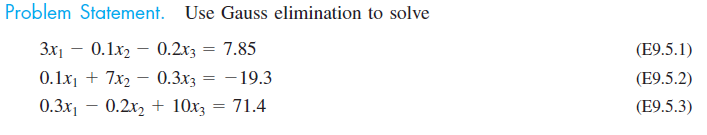Musyafi Albar

From ccitonlinewiki
Revision as of 12:29, 15 January 2021 by Musyafi Albar (talk | contribs)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Jump to: navigation, search
Biodata
Mus.jpg
Nama Musyafi Albar
NPM 1906379094
Email musyafi.albar@ui.ac.id


Musyafi Albar

Perkenalkan nama saya Musyafi Albar (NPM 1906379094) biasa dipanggil Mus. Saya Adalah mahasiswa Teknik Mesin angkatan 2019 dari Fakultas Teknik Universitas Indonesia. Saya memiliki ketertarikan kepada bidang mesin karena dirasa jurusan tersebut memiliki rana yang luas untuk dunia kerjanya. Pada Pelajaran metnum sebelumnya saya telah mempelajari tentang persamaan, istilah algoritma, kurva, regresi, differensial, parsial

Catatan Minggu Pertama (11 November 2020)

Tujuan Pembelajaran

  • Memahami konsep dan prinsip dasar metode numerik
  • Dapat menerapkan pemahaman yang didapatkan dalam mata kuliah Metode Numerik
  • Mampu menerapkan pemahaman metode numerik dalam bidang keteknikan
  • Membentuk kita menjadi orang yang lebih beradab

Manfaat Belajar bagi Diri Saya Sendiri

Menurut saya, pembelajaran adalah suatu proses penambahan kualitas diri. Saya merasa dengan belajar kita bisa memahami berbagai macam hal yang dapat menambah kualitas pada diri sendiri. Hasil dari penambahan kualitas tersebut berupa pemanfaatan hal yang telah dipelajari, diaplikasikan di kehidupan nyata. Sebagai contoh kita belajar pendidikan dari sd hingga sma untuk menambah kualitas diri dan digunakan untuk menempuh belajar di Kuliah.

Komputer dalam Metode Numerik

Komputer merupakan alat hitung yang cepat. Kualitas dari komputer bergantung pada spesifikasi pembuatannya. Penggunaan dari alat tersebut juga bergantung pada pemakainya.

Tugas 1

Berikut merupakan video penjelasan aplikasi OpenModelica untuk menyelesaikan suatu Sistem Persamaan

Catatan Minggu kedua (18 November 2020)

Pembahasan

Pada kuliah pertemuan ke 2 dibahas tentang penggunaan Openmodelica

Sesi Tanya jawab :

Mengapa menggunakan openmodelica : Karena openmodelica merupakan bahasa permodolen yang gratis. Apa Perbedaan constan real dengan parameter real : untuk mengganti variabel pada simulasi jika menggunakan comand constan real diperlukan simulate ulangsedangkan dengan menggunakan comand parameter real tidak perlu simulate ulang hanya dengan mengganti variabel xnya

Penyataan Penting Openmodelica merupakan object oriented. Pada modelica specialization model digunakan untuk menyelesaikan suatu fungsi sedangankan class digunakan untuk penggabungan fungsi-fungsi. Setiap specializtion digunakan untuk tujuan yang berbeda-beda dengan mempunyai kelebihan dan kelemahan.

Tugas 2

Membuat open modecalica dengan specializtion Class persamaan aljabar simultan

function 

function p
input Real A[4,4];
input Real B[4];
output Real X[4]; 
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
end p;

class 

class o
parameter Real P[4,4]=[8,-9,1,-8;
                      -3,-1,5,4;
                      -2,-1,-3,8;
                      -2,-8,-1,2];
Q[4]={80,7,-30,18};
Real X[4];
equation
X=o(P,Q);
end SPL;

Video tugas

Catatan Minggu ketiga (25 November 2020)

Pengaplikasian dalam Open Modelica, kita akan membuat code untuk menyelesaikan persamaan 9.12 pada buku Chapra yaitu mengenai eliminasi Naïve Gauss. Pseudocode untuk eliminasi Naïve Gauss diberikan pada Fig.9.4:

1.PNG

pseudocode dibuat kedalam bahasa Open Modelica

....

Penggunaan code dengan menyelesaikan

21.PNG

....

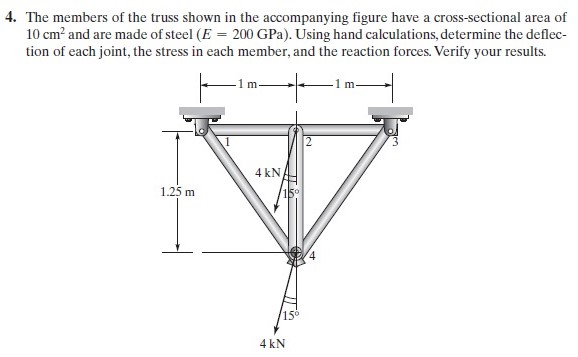
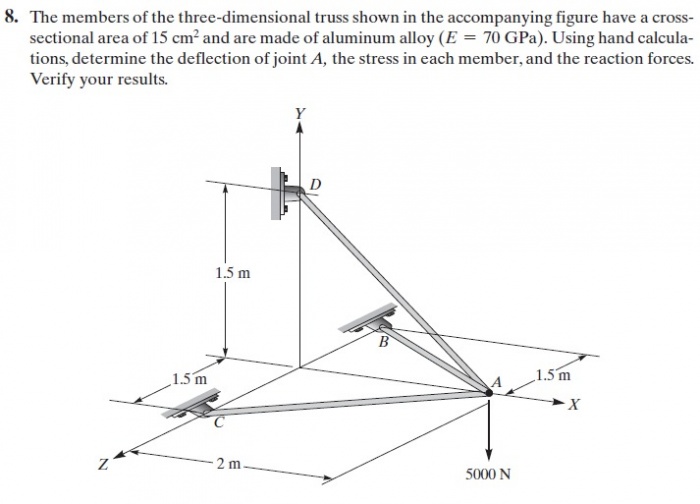
Tugas Minggu ketiga (25 November 2020)

menyelesaikan permalasahan truss berikut:

Problem 3 tedi veradino.jpeg

Class 

class Trusses_Tugas3_d29

parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //m^2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global displacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary condition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between trusses
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrices
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=0; //degree between trusses
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrices
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=90; //degree between trusses
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrices
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
 
//truss 4
parameter Real X4=90+38.6598; //degree between trusses
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrices
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=90-38.6598; //degree between trusses
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrices
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];

/*
for each truss, ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses_Tugas3_d29;

Function Stiffness_Matrices 

function Stiffness_Matrices

input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
    
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness_Matrices;

Function Gauss-Jordan 

function Gauss_Jordan

input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;

algorithm
X:=Modelica.Math.Matrices.solve(A,B);

for i in 1:N loop
  if abs(X[i]) <= float_error then
    X[i] := 0;
  end if;
end for;

end Gauss_Jordan;

Function Reaction_Trusses 

function Reaction_Trusses

input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
 if abs(X[i,1]) <= float_error then
   X[i,1] := 0;
 end if;
end for;

for i in 1:N loop
 Sol[i]:=X[i,1];
end for;

end Reaction_Trusses;

Function Local_Global 

function Local_Global

input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
 for j in 1:B loop
     G[i,j]:=0;
 end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];

end Local_Global;

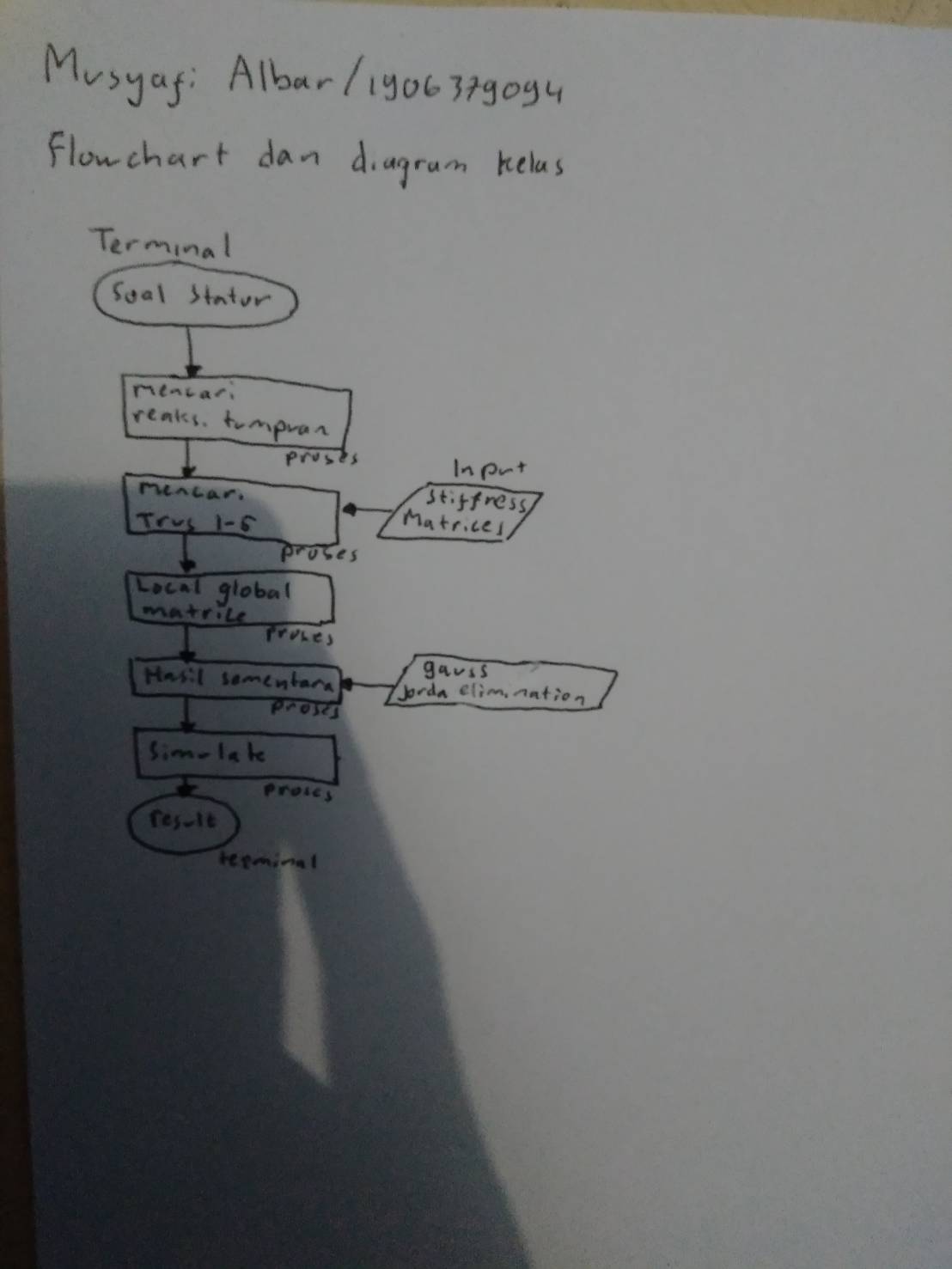
Quiz class diagram dan flowchart Minggu keempat (2 Desember 2020)

253564.jpg

Tugas Minggu keempat (2 Desember 2020)

Penyelesaikan permasalahan truss 3D dengan membuat class diagram, flowchart, dan penyelesaiannya pada Open Modelica.

No8 d29.jpeg

class diagram dan flowchart

264969.jpg

Open Modelica langkah pertama membuat class berisi data yang diketahui dan perhitungan-perhitungannya

Class 

class Tugas
  parameter Real [:,9] inisiasi = [1, 1, 2, -0.8,    0, -0.6, 15e-4, 70e9, 2.5;
                                   2, 1, 3, -0.8, -0.6,    0, 15e-4, 70e9, 2.5;
                                   3, 1, 4, -0.8,    0,  0.6, 15e-4, 70e9, 2.5];
  parameter Integer [:,2] node = [1, 2;
                                  1, 3;
                                  1, 4];
  parameter Integer y = size(node,1);
  parameter Integer x = 3*(size(node_load,1));
  parameter Integer z = size(Boundary,1);
  parameter Integer [:] Boundary = {2,3,4};
  parameter Real [:,4] node_load = [1, 0, -5000, 0;
                                    2, 0,     0, 0;
                                    3, 0,     0, 0;
                                    4, 0,     0, 0];
  parameter Real [x] load = {0,-5000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
  Real [y] k;
  Real [y,6,6] Ke;
  Real [y,x,x] Kg;
  Real [x,x] KgTot;
  Real [x,x] KgB;
  Real [x] U;
  Real [x] R;
  
equation
 k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
 Ke = StiffnessMatrixElement(inisiasi);
 Kg = StiffnessMatrixGlobal(node, x, y, Ke);
 KgTot = SumStiffnessMatrixGlobal(x, y, Kg);
 KgB = BoundaryStiffnessMatrixGlobal(x, z, KgTot, Boundary);
 U = GaussJordan(x, KgB, load);
 R = ReactionForce(x, KgTot, U, load);

end Tugas;

Selanjutnya membuat function kekakuan dalam class menggunakan rumus k=AE/L di setiap batang

Function StiffnessMatrixElement 

function StiffnessMatrixElement

 input Real [:,9] inisiasi_mat;
 output Real [size(inisiasi_mat,1),6,6] Ke_mat;

 protected
   Real cos_x;
   Real cos_y;
   Real cos_z;
   Real [6] StiffTrig;
   Real [6,6] StiffTrans;
   Real [size(inisiasi_mat,1)] k_vec;

algorithm
 k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};

 // Finding stiffness matrix of each element member
 for i in 1:size(inisiasi_mat,1) loop

 // Clearing the matrices
 StiffTrig := zeros(6);
 StiffTrans := zeros(6,6);
 
 // Converting degrees to radians
 cos_x := inisiasi_mat[i,4];
 cos_y := inisiasi_mat[i,5];
 cos_z := inisiasi_mat[i,6];

 // {cos^2, sin^2, sincos}
 StiffTrig := {(cos_x)^2,
               (cos_y)^2,
               (cos_z)^2,
               (cos_x*cos_y),
               (cos_x*cos_z),
               (cos_y*cos_z)};
 
 // Construct stiffness transformation matrix
 StiffTrans := [  StiffTrig[1],    StiffTrig[4],    StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
                  StiffTrig[4],    StiffTrig[2],    StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
                  StiffTrig[5],    StiffTrig[6],    StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
               -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5],    StiffTrig[1],    StiffTrig[4],    StiffTrig[5];
               -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6],    StiffTrig[4],    StiffTrig[2],    StiffTrig[6];
               -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3],    StiffTrig[5],    StiffTrig[6],    StiffTrig[3]];
               
 // Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
 for m in 1:6 loop
   for n in 1:6 loop
     Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
   end for;
 end for;

end for;
end StiffnessMatrixElement;

Setelah itu matriks 6x6 K tersebut akan dibuat menjadi matriks 12x12 sesuai dengan jumlah batang (3) * jumlah node (4). Ini disebut matriks kekakuan global (Kg).

Function StiffnessMatrixGlobal 

function StiffnessMatrixGlobal
 input Integer [:,2] n;
 input Integer x;
 input Integer y;
 input Real [y,6,6] Ke_mat; 
 output Real [y,x,x] Kg_mat;
 
algorithm
 for i in 1:y loop
   for a in 1:x loop
     for b in 1:x loop
       Kg_mat[i,a,b]:=0;
     end for;
   end for;
  end for;

 for i in 1:y loop
   Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
   Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
   Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
   Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
   Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];

   Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
   Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
   Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
   Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
   Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];

   Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
   Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
   Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
   Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
   Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];

   Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
   Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
   Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
   Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
   Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
 end for;
end StiffnessMatrixGlobal;

Selanjutnya, matriks kekakuan global setiap batang dijumlahkan untuk mendapat matriks kekakuan global total(KgTot)

Function SumStiffnessMatrixGlobal 

function SumStiffnessMatrixGlobal
 input Integer x;
 input Integer y;
 input Real [y,x,x] Kg_mat;
 output Real [x,x] KgTot_mat;
 
algorithm
  for a in 1:x loop
   for b in 1:x loop
     KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
    end for;
   end for;

end SumStiffnessMatrixGlobal;

Kemudian boundary diterapkan pada matriks kekakuan global total. Pada kasus ini, node 2,3, dan 4 merupakan pinned. Sehingga U2X=U2Y=U2Z=U3X=U3Y=U3Z=U4X=U4Y=U4Z=0.

Function BoundaryStiffnessMatrixGlobal 

function BoundaryStiffnessMatrixGlobal
 input Integer x;
 input Integer z;
 input Real [x,x] KgTot_met;
 input Integer[z] Boundary_met;
 output Real [x,x] KgB_met;
 
algorithm
 for a in 1:x loop
   for b in 1:x loop
    KgB_met[a,b] := KgTot_met [a,b];
   end for;
  end for; 
 
 for i in 1:x loop
  for a in 1:z loop
   for b in 0:2 loop
     KgB_met[3*(Boundary_met[a])-b,i]:=0;
   end for;
  end for;
 end for;

 for a in 1:z loop
   for b in 0:2 loop
     KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
   end for;
 end for;
  
end BoundaryStiffnessMatrixGlobal;

Untuk mencari nilai displacement(U) lainnya menggunakan eliminasi Gauss Jordan dengan persamaan XU=F. Dengan X adalah matriks K global yang sudah menerapkan boundary(KgB) dan F adalah eksternal load.

Function GaussJordan 

function GaussJordan
 input Integer x;
 input Real [x,x] KgB_met;
 input Real [x] load_met;
 output Real [x] U_met;
 
 protected
 Real float_error = 10e-10;

algorithm
 U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);

 for i in 1:x loop
   if abs(U_met[i]) <= float_error then
    U_met[i] := 0;
   end if;
 end for;

end GaussJordan;

Sedangkan untuk mencari reaction menggunakan persamaan R=Kg*U - F.

Function ReactionForce 

function ReactionForce
 input Integer x;
 input Real [x,x] KgTot_met;
 input Real [x] U_met;
 input Real [x] load_met;
 output Real [x] R_met;

algorithm
 R_met := (KgTot_met*U_met)-load_met;
end ReactionForce;

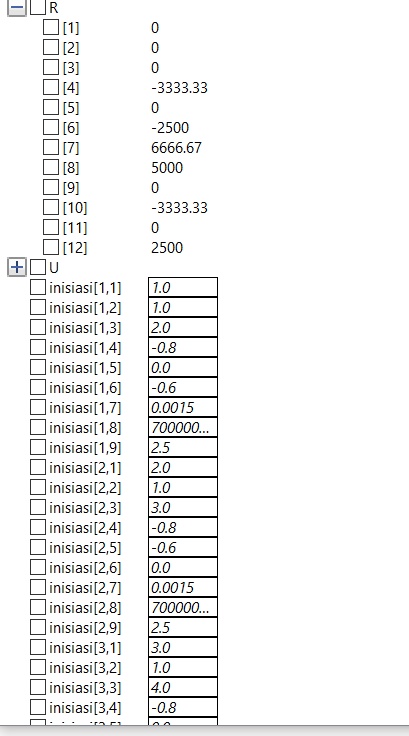
Function-function tersebut akan dipanggil ke dalam sebuah class untuk penyelesaiannya. Pada class akan diinput data-data yang telah docari pada langkah pertama. Dan didapat 1223.PNG

Tugas Minggu Enam (16 Desember 2020)

Tema : Aplikasi Metoda Numerik dalam Optimasi Desain Struktur Rangka Sederhana

Sinopsis Tugas Besar

Dalam tugas besar ini kami diminta untuk mendesain rangka sesuai yang tertera dibawah dengan menggunakan rangka yang optimal dan cost yang minimum

Soaltubesy.jpeg Soaltubes1.jpeg

Adapun Hal yang Harus Diperhitungkan sebagai Plotting

  • A Harga material di dapat dari nilai optimum defleksi dan cross section
  • B Material (Elastisitas properti)
  • C Area Cross Section Truss (L profile/truss siku), luas cross section sebagai X
  • D Defleksi sebagai Y

Perhitungan Displacement, Reaction Force, Stress, dan Safety Factor

model Trusses3DTugasBesar 

 //define initial variable
 parameter Integer Points=size(P,1); //Number of Points
 parameter Integer Trusses=size(C,1); //Number of Trusses
 parameter Real Yield=292e6; //Yield Strength (Pa)
 parameter Real Area=0.000224;   //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
 parameter Real Elas=197e9;     //Elasticity SS 201  (Pa)
 //define connection
 parameter Integer C[:,2]=[1,5; 
                           2,6;
                           3,7;
                           4,8;
                           5,6;  //1st floor
                           6,7;  //1st floor
                           7,8;  //1st floor
                           5,8;  //1st floor
                           5,9;
                          6,10;
                          7,11;
                          8,12;
                          9,10; //2nd floor
                         10,11;//2nd floor 
                          11,12;//2nd floor
                          9,12; //2nd floor
                          9,13;
                          10,14;
                          11,15;
                         12,16;
                         13,14;//3rd floor
                         14,15;//3rd floor
                         15,16;//3rd floor
                         13,16];//3rd floor
                                                             
 //define coordinates (please put orderly)
 parameter Real P[:,6]=[0.3,-0.375,0,1,1,1;     //1
                       -0.3,-0.375,0,1,1,1;    //2
                       -0.3,0.375,0,1,1,1;     //3
                       0.3,0.375,0,1,1,1;      //4
                          
                       0.3,-0.375,0.6,0,0,0;   //5
                       -0.3,-0.375,0.6,0,0,0;  //6
                       -0.3,0.375,0.6,0,0,0;   //7
                       0.3,0.375,0.6,0,0,0;    //8
                           
                       0.3,-0.375,1.2,0,0,0;   //9
                       -0.3,-0.375,1.2,0,0,0;  //10  
                       -0.3,0.375,1.2,0,0,0;   //11
                       0.3,0.375,1.2,0,0,0;    //12
                           
                       0.3,-0.375,1.8,0,0,0;   //13
                       -0.3,-0.375,1.8,0,0,0;  //14
                       -0.3,0.375,1.8,0,0,0;   //15
                       0.3,0.375,1.8,0,0,0];   //16
                           
 //define external force (please put orderly)
 parameter Real F[Points*3]={0,0,0,
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,0, 
                             0,0,-500, 
                             0,0,-1000, 
                             0,0,-1000, 
                             0,0,-500}; 
 //solution
 Real displacement[N], reaction[N];
 Real check[3];
 Real stress1[Trusses];
 Real safety[Trusses];
 Real dis[3];
 Real Str[3]; 
 protected
 parameter Integer N=3*Points;
 Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 Real err=10e-10, ers=10e-4;

algorithm 

 //Creating Global Matrix
 G:=id;
 for i in 1:Trusses loop
   for j in 1:3 loop
     q1[j]:=P[C[i,1],j];
     q2[j]:=P[C[i,2],j];
   end for;      
     //Solving Matrix
     L:=Modelica.Math.Vectors.length(q2-q1);
     cx:=(q2[1]-q1[1])/L;
     cy:=(q2[2]-q1[2])/L;
     cz:=(q2[3]-q1[3])/L; 
     X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                       cy*cx,cy^2,cy*cz;
                      cz*cx,cz*cy,cz^2];
     //Transforming to global matrix
     g:=zeros(N,N); 
     for m,n in 1:3 loop
       g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
       g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
       g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
       g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
     end for;  
   G_star:=G+g;
   G:=G_star;
 end for;
 //Implementing boundary
 for x in 1:Points loop
   if P[x,4] <> 0 then
     for a in 1:Points*3 loop
       G[(x*3)-2,a]:=0;
       G[(x*3)-2,(x*3)-2]:=1;
     end for;
   end if;
   if P[x,5] <> 0 then
     for a in 1:Points*3 loop
       G[(x*3)-1,a]:=0;
       G[(x*3)-1,(x*3)-1]:=1;
     end for;
   end if;
   if P[x,6] <> 0 then
     for a in 1:Points*3 loop
       G[x*3,a]:=0;
       G[x*3,x*3]:=1;
     end for;
   end if;
 end for;
 //Solving displacement
 displacement:=Modelica.Math.Matrices.solve(G,F);
 //Solving reaction
 reaction:=(G_star*displacement)-F;
 //Eliminating float error
 for i in 1:N loop
   reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
   displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 end for;
 //Checking Force
 check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});  
 for i in 1:3 loop
   check[i] := if abs(check[i])<=ers then 0 else check[i];
 end for;
 //Calculating stress in each truss
 for i in 1:Trusses loop
   for j in 1:3 loop
     q1[j]:=P[C[i,1],j];
     q2[j]:=P[C[i,2],j];
     dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
   end for;      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
                cy*cx,cy^2,cy*cz;
                cz*cx,cz*cy,cz^2];   
   Str:=(X*dis);
   stress1[i]:=Modelica.Math.Vectors.length(Str);
 end for;
 //Safety factor
 for i in 1:Trusses loop
   if stress1[i]>0 then
     safety[i]:=Yield/stress1[i];
   else
     safety[i]:=0;
   end if; 
 end for;

end Trusses3DTugasBesar;

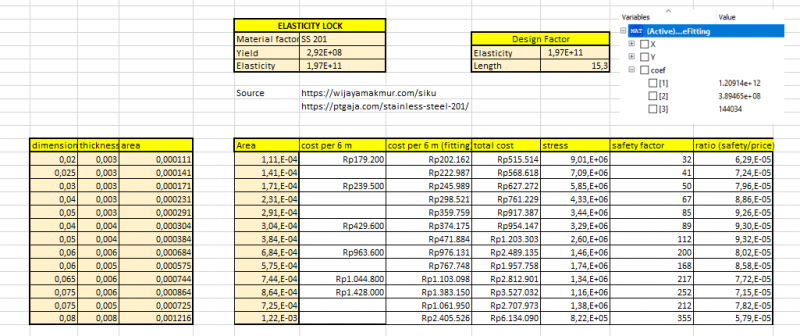
Perhitungan Rasio Perbandingan Safety Factor dan Biaya

selanjutnya diperlukan pendataan guna mendapatkan banyak data yang diperlukan dalam proses curve fitting, yang nantinya akan digunakan untuk optimasi. data saya kumpulkan dengan melihat beberapa website referensi berikut:

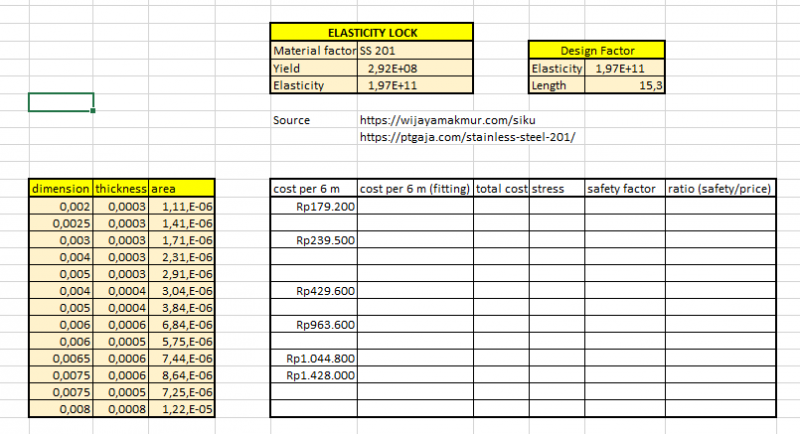
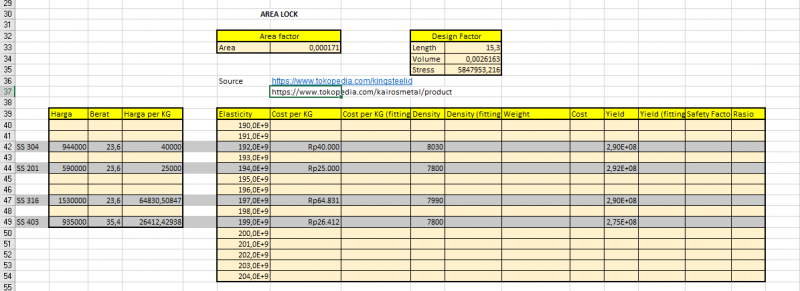
dengan data yang didapatkan pada 4 website tersebut, saya berhasil mengumpulkan data sementara menjadi sebagai berikut

ElasLock.PNG
AreaLock.PNG

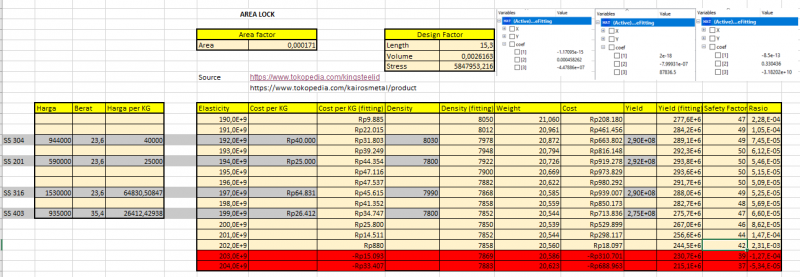
terlihat dari gambar bahwa masih banyak sekali data yang kosong (tidak memiliki input. oleh karena itu, dibutuhkan curve fitting untuk mengisi kekosongan tersebut. fungsi dari dilakukannya curve fitting adalah untuk mengetahui nilai sebuah input yang tidak diketahui sebelumnya. berikut fungsi yang akan dipanggil untuk proses curve fitting

function FuncCurveFitting 

 input Real X[:];
 input Real Y[size(X,1)];
 input Integer order=2;
 output Real Coef[order+1];

 protected
 Real Z[size(X,1),order+1];
 Real ZTr[order+1,size(X,1)];
 Real A[order+1,order+1];
 Real B[order+1];

algorithm 

 for i in 1:size(X,1) loop
   for j in 1:(order+1) loop
     Z[i,j]:=X[i]^(order+1-j);
   end for;
 end for;
 ZTr:=transpose(Z);

 A:=ZTr*Z;
 B:=ZTr*Y;
 Coef:=Modelica.Math.Matrices.solve(A,B);

end FuncCurveFitting;

untuk menjalankan fungsi tersebut, tentunya kita memerlukan model untuk memanggil fungsi tersebut. berikut adalah model nya

model CurveFitting 

 parameter Real X[6]={0.000111, 0.000171, 0.000304, 0.000684, 0.000744, 0.000864};
 parameter Real Y[6]={179200, 239500, 429600, 963600, 1044800, 1428000};
 Real coef[3];

equation 

 coef=FuncCurveFitting(X,Y,2);

end CurveFitting;

model tersebut dapat digunakan untuk curve fitting berkali-kali. hanya perlu menyesuaikan nilai X dan Y yang diketahui saja. sebagai contoh, code diatas merupakan code curve fitting untuk mencari besar cost per 6 meter. setelah mendapatkan nilai dari hasil curve fitting, data yang kita miliki menjadi sebagai berikut:

ElasLockFix.PNG
AreaLockFix.PNG

dengan demikian kita telah memiliki sejumlah data yang dapat diolah dalam proses optimasi

UAS

268808.jpg 268809.jpg

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Musyafi_Albar&oldid=56545"