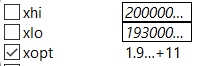John Audrick
| John Audrick | |
|---|---|

| |
| Nama Lengkap | John Audrick |
| Nama Panggilan | John |
| NPM | 1806201043 |
| Tempat, tanggal lahir | Jakarta, 22 Februari 2000 |
| Jurusan | Teknik Mesin 2018 |
Contents
Mengenal John Audrick
Saya adalah mahasiswa FTUI angkatan 2018 dari jurusan Teknik Mesin dan saya adalah salah satu ciptaan terbaik dari Tuhan Yang Maha Esa, karena pada prinsipnya Tuhan Yang Maha Esa itu mendesain manusia dengan sebaik-baiknya makhluk. Saya termotivasi untuk mengembangkan diri saya dengan sebaik-baiknya dan dapat menjadi berguna untuk masyarakat luas dan terutama untuk keluarga saya.
Materi yang telah dipelajari
Perkuliahan Metode Numerik yang telah di isi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Beberapa topik yang dibahas yaitu:
Pseudocode
Sistem Persamaan
Turunan Numerik
Metode Newton Rhapson, Secant, dan Bisection
Regresi Linear
Interpolasi
Setelah UTS, perkuliahan Metode Numerik diisi oleh Bapak Dr. Ir. Ahmad Indra Siswantara
Minggu 1 (11 November 2020)
- Metode numerik memiliki beberapa prinsip dasar seperti aljabar simultan, istiliah algoritma, istilah regresi, cuve fitting. persamaan diferensial, dan lain-lain.
- Kita harus bisa menerapkan pemahaman konsep didalam permodelan numerik. Permodelan numerik menyelesaikan masalah dengan metode numerik.
- Contohnya adalah kita mengerti persamaan aljabar simultan dan mampu menerapkan metode numerik dalam persoalan perteknikan.
Tujuan dari metode numerik adalah :
1. Memahami konsep dan prinsip dasar dalam metode numerik. contohnya adalah persamaan aljabar, agoritma, pencocokan kurva, persamaan diferensia, parsial, dan lain lain.
2. Mengerti aplikasi metode numerik.
3. Mampu Menerapkan metode numerik dalam persoalan teknik.
4. Mendapat nilai tambah/adab sehingga kita menjadi orang yang lebih beradab.
Pada dasarnya, manusia merupakan makhluk ciptaan Tuhan yang sangat baik. Komputer merupakan ciptaan manusia dan memiliki banyak kelebihan, seperti kemampuan menghitung yang cepat. Namun komputer memiliki limitasi hal ini diberikan contoh dengan membagi 1/10^-400 dimana komputer tidak dapat mengeluarkan hasil tapi kita mengetahui hasilnya 10^400. Namun manusiapun memiliki limitasinya juga hal ini juga dijelaskan dengan contoh 1/0 dimana tidak ada manusia yang tau, namun hanya Tuhan yang mengetahui jawaban tersebut. Hal ini membuktikan bahwa manusia hanya merupakan makhluk ciptaan Tuhan dan manusia tidak boleh sombong dengan apa yang diketahui, karena sesungguhnya hanya Tuhan yang merupakan sumber segala ilmu dan maha tahu.
Tugas Minggu 1
Pada minggu pertama ini saya mempelajari aplikasi Open Modelica melalui video berikut
https://www.youtube.com/watch?v=m0Ahs8fEN28
https://www.youtube.com/watch?v=esSMzMCFwbo
Hasil pembelajaran saya, diaplikasikan melalui video sebagai berikut
video saya :
Tugas Minggu 2
Untuk tugas pada minggu kedua, kami diminta untuk membuat program menggunakan suatu fungsi panggil, pada saat kelas menggunakan persamaan aljabar simultan dan variable array. Persamaan Aljabar Simultan adalah persamaan yang memiliki banyak variabel dan banyak persamaan. Variabel ini harus dicari nilainya. Variable array merupakan viarabel dengan bebereapa data nilai didalamnya. Pada tugas kali ini, saya menggunakan persamaan dengan 4 variabel dan 4 persamaan.
Minggu 3
Pada pertemuan pada minggu ketiga, kami dijelaskan tentang pseudocode gauss elimination secara manual. Saya membuat tugas 2 dengan fungsi yang sudah disediakan open modelica. Hal ini tidak sesuai dengan yang di harapkan. Pak Dai menginginkan kami bisa membuat pseudocode untuk gauss jordan secara mandiri tanpa menggunakan fungsi yang sudah disediakan dari OpenModelica. Pak Dai meminta Christo untuk menjelaskan pseudocode untuk gauss. Christo adalah salah seorang teman dari angkatan saya yang juga menggambil kelas metode numerik Pak Dai pada semester ini. Christo menjelaskan dengan baik pseudocode untuk gauss. Untuk minggu ketiga kami diminta mengerjakan soal truss dari example 3.1. berikut merupakan pseudocode yang saya usahakan.
Tugas Truss
class TrussPR
parameter Integer N=8;
parameter Real A=0.001;
parameter Real E=200*10e9;
Real KG[N,N]; //ukuran matriks (global)
Real KGinitial[N,N];
Real Sol[N];
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N];
Real SolMat[N,1];
Real XMat[N,1];
Real L1 = 1;
Real L2 = 1;
Real L3 = 1.6;
Real L4 = 1.25;
Real L5 = 1.6;
Real teta1 =degtorad(0);
Real teta2 =degtorad(0);
Real teta3 =degtorad(231.34);
Real teta4 =degtorad(270);
Real teta5 =degtorad(308.66);
//boundary condition
Integer b1=1;
Integer b2=3;
//Truss 1
parameter Real X1=0;
Real k1=A*E/1;
Real K1[4,4];
Integer p1a = 1;
Integer p1b = 2;
Real KG1[N,N];
//truss 2
parameter Real X2=0;
Real k2=A*E/1;
Real K2[4,4];
Integer p2a=2;
Integer p2b=3;
Real KG2[N,N];
//truss 3
parameter Real X3=90;
Real k3=A*E/1.25;
Real K3[4,4];
Integer p3a=2;
Integer p3b=4;
Real KG3[N,N];
//truss 4
parameter Real X4=90+38.6598;
Real k4=A*E/1.6;
Real K4[4,4];
Integer p4a=1;
Integer p4b=4;
Real KG4[N,N];
//truss 5
parameter Real X5=90-38.6598;
Real k5=A*E/1.6;
Real K5[4,4];
Integer p5a=3;
Integer p5b=4;
Real KG5[N,N];
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
KG:=KG1+KG2+KG3+KG4+KG5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end TrussPR;
Stiffness Matricies
function Stiffness_Matrices
input Real A; Real Y; output Real X[4,4]; Real float_error = 10e-10; protected final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi; X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
Local Global
function Local_Global
input Real Y[4,4]; input Integer M; input Integer p1; input Integer p2; output Real G[M,M];
algorithm
for i in 1:M loop
for j in 1:M loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2]; G[2*p1-1,2*p1-1]:=Y[1,1]; G[2*p1,2*p1-1]:=Y[2,1]; G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4]; G[2*p2-1,2*p2-1]:=Y[3,3]; G[2*p2,2*p2-1]:=Y[4,3]; G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2]; G[2*p2-1,2*p1-1]:=Y[3,1]; G[2*p2,2*p1-1]:=Y[4,1]; G[2*p2-1,2*p1]:=Y[3,2];
end Local_Global;
Reaction Trusses
function Reaction_Trusses
input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10;
algorithm X:=A*B-C;
for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for;
for i in 1:N loop Sol[i]:=X[i,1]; end for;
end Reaction_Trusses;
Gauss Jordan
function GJ
input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; protected
Real float_error = 10e-10;
algorithm X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end GJ;
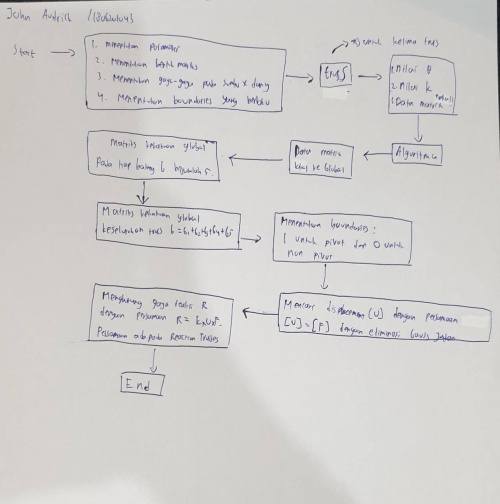
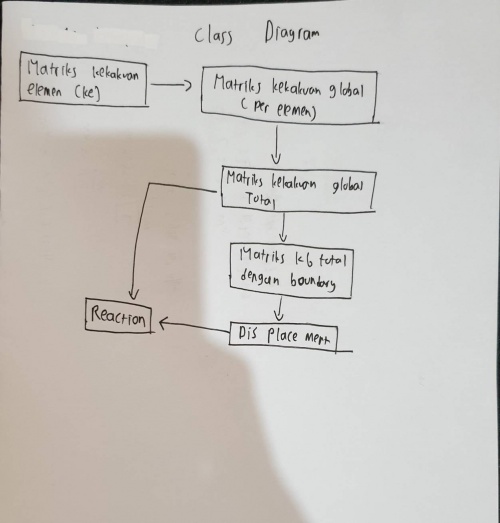
Membuat Diagram Class dan Flowchart untuk tugas coding pada minggu ketiga dari Josiah Enrico
1. Membuat Parameter yang berlaku pada kondisi tersebut.
2. Menentukan bentuk matriks
3. memasukan gaya pada x dan y
4. membuat boundary
Tugas Minggu ke 4
Matrix Global
function BoundaryStiffnessMatrixGlobal
input Integer x;
input Integer z;
input Real [x,x] KgTot_met;
input Integer[z] Boundary_met;
output Real [x,x] KgB_met;
algorithm
for a in 1:x loop
for b in 1:x loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
for i in 1:x loop
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*(Boundary_met[a])-b,i]:=0;
end for;
end for;
end for;
for a in 1:z loop
for b in 0:2 loop
KgB_met[3*Boundary_met[a]-b,3*Boundary_met[a]-b]:=1;
end for;
end for;
function f_obj3 import Modelica.Math; input Real x; input Real y;
algorithm y := 2*Math.sin(x)-x^2/10; end f_obj3;
Eliminasi Gauss Jordan
function GaussJordan input Integer x; input Real [x,x] KgB_met; input Real [x] load_met; output Real [x] U_met; protected Real float_error = 10e-10;
algorithm U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:x loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
end BoundaryStiffnessMatrixGlobal;
Reaction Force
function ReactionForce input Integer x; input Real [x,x] KgTot_met; input Real [x] U_met; input Real [x] load_met; output Real [x] R_met;
algorithm R_met := (KgTot_met*U_met)-load_met; end ReactionForce;
Stiffness Matrix Element
function StiffnessMatrixElement
input Real [:,9] inisiasi_mat; output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected Real cos_x; Real cos_y; Real cos_z; Real [6] StiffTrig; Real [6,6] StiffTrans; Real [size(inisiasi_mat,1)] k_vec;
algorithm
k_vec := {(inisiasi_mat[i,7] * inisiasi_mat[i,8] / inisiasi_mat[i,9]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices StiffTrig := zeros(6); StiffTrans := zeros(6,6); // Converting degrees to radians cos_x := inisiasi_mat[i,4]; cos_y := inisiasi_mat[i,5]; cos_z := inisiasi_mat[i,6];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for; end StiffnessMatrixElement;
Stiffness matrix global
function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
for i in 1:y loop
for a in 1:x loop
for b in 1:x loop
Kg_mat[i,a,b]:=0;
end for;
end for;
end for;
for i in 1:y loop Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; end for; end StiffnessMatrixGlobal;
Sum Stiffness Global
function SumStiffnessMatrixGlobal
input Integer x;
input Integer y;
input Real [y,x,x] Kg_mat;
output Real [x,x] KgTot_mat;
algorithm
for a in 1:x loop
for b in 1:x loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
Minggu Ke 5
Pada minggu ke 5 ini, pada minggu kelima adalah kelas pengganti. Pak Dai meminta kita membuat muhasabah dan melakukan penilaian terhadap diri sendiri terhadap kemampuan kita. Kami mengisi nilai yang kami rasa pantas untuk kami dapatkan sesuai dengan kemampuan kita. Selain itu kami juga harus bisa menjelaskan apa saja yang telah kami pelajaran sebagai bukti dari ilmu yang telah kita kuasai.
Minggu ke 6
Pada minggu ke 6 ,kami mempelajari tentang optimasi. Bu Chandra menjelaskan tentang materi ini, penjelasan Bu Chandra mengenai kasus optimasi serta pseudocode dari kasus tersebut. Optimasi merupakan sebuah proses mencari nilai paling efisien dari suatu sistem. Berikut adalah Pseudocode dari Open Modelica
Fungsi Object
function FungsiObjek input Real x; output Real y;
algorithm
y:= 2*Modelica.Math.sin(x)-x^2/10;
end FungsiObjek;
fungsi ini merupakan fungsi panggil.
GoldenMethod.mo model GoldenMethod
parameter Integer n = 8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real f1[n]; Real f2[n]; Real xopt; Real yopt; Real d;
algorithm xup := 4; xlow := 0;
for i in 1:n loop d:=((5^(1/2)-1)/2) * (xup-xlow); x1[i] := xlow+d; x2[i] := xup-d; f1[i] := FungsiObjek(x1[i]); f2[i] := FungsiObjek(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow := x2[i];
xopt := xup;
yopt := f1[i];
else
xlow :=xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end GoldenMethod;
Model ini menggunakan fungsi untuk memanggil model yang sudah ada.
Minggu 7
Pada Minggu ke 7 dilaksanakan kuis. Pada kuis ini kami diminta untuk membuat defleksi dari tugas besar yang diberikan. Berikut merupakan Pseudocodenya
class KuisMetnum
//Urutan Penulisan: [Truss, Node 1, Node 2, Cx, Cy, Cz, A, E, L]
parameter Real [:,9] inisiasi = [ 1, 1, 2, 0, 1, 0, 9e-4, 190e9, 0.75;
2, 2, 3, 1, 0, 0, 9e-4, 190e9, 0.6;
3, 3, 4, 0, -1, 0, 9e-4, 190e9, 0.75;
4, 1, 4, 1, 0, 0, 9e-4, 190e9, 0.6;
5, 5, 6, 0, 1, 0, 9e-4, 190e9, 0.75;
6, 6, 7, 1, 0, 0, 9e-4, 190e9, 0.6;
7, 7, 8, 0, -1, 0, 9e-4, 190e9, 0.75;
8, 5, 8, 1, 0, 0, 9e-4, 190e9, 0.6;
9, 9, 10, 0, 1, 0, 9e-4, 190e9, 0.75;
10, 10, 11, 1, 0, 0, 9e-4, 190e9, 0.6;
11, 11, 12, 0, -1, 0, 9e-4, 190e9, 0.75;
12, 9, 12, 1, 0, 0, 9e-4, 190e9, 0.6;
13, 1, 5, 0, 0, 1, 9e-4, 190e9, 0.75;
14, 2, 6, 0, 0, 1, 9e-4, 190e9, 0.75;
15, 3, 7, 0, 0, 1, 9e-4, 190e9, 0.75;
16, 4, 8, 0, 0, 1, 9e-4, 190e9, 0.75;
17, 5, 9, 0, 0, 1, 9e-4, 190e9, 0.75;
18, 6, 10, 0, 0, 1, 9e-4, 190e9, 0.75;
19, 7, 11, 0, 0, 1, 9e-4, 190e9, 0.75;
20, 8, 12, 0, 0, 1, 9e-4, 190e9, 0.75;
21, 9, 13, 0, 0, 1, 9e-4, 190e9, 0.3;
22, 10, 14, 0, 0, 1, 9e-4, 190e9, 0.3;
23, 11, 15, 0, 0, 1, 9e-4, 190e9, 0.3;
24, 12, 16, 0, 0, 1, 9e-4, 190e9, 0.3];
parameter Integer [:,2] node = [ 1, 2;
2, 3;
3, 4;
1, 4;
5, 6;
6, 7;
7, 8;
5, 8;
9, 10;
10, 11;
11, 12;
9, 12;
1, 5;
2, 6;
3, 7;
4, 8;
5, 9;
6, 10;
7, 11;
8, 12;
9, 13;
10, 14;
11, 15;
12, 16];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {13,14,15,16};
parameter Real [:,4] node_load = [ 1, 0, 1000, 0;
2, 0, 1000, 0;
3, 0, 500, 0;
4, 0, 500, 0;
5, 0, 0, 0;
6, 0, 0, 0;
7, 0, 0, 0;
8, 0, 0, 0;
9, 0, 0, 0;
10, 0, 0, 0;
11, 0, 0, 0;
12, 0, 0, 0;
13, 0, 0, 0;
14, 0, 0, 0;
15, 0, 0, 0;
16, 0, 0, 0];
parameter Real [x] load = {0, 1000, 0,
0, 1000, 0,
0, 500, 0,
0, 500, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = MatriksKekakuanElemen(inisiasi);
Kg = MatriksKekakuanGlobal(node, x, y, Ke);
KgTot = MatriksTotalKekakuanGlobal(x, y, Kg);
KgB = MatriksKekakuanGlobalDenganBoundary(x, z, KgTot, Boundary);
U = FungsiGaussJordan(x, KgB, load);
R = FungsiReactionForce(x, KgTot, U, load);
end KuisMetnum;
Tugas Besar Metode Numerik
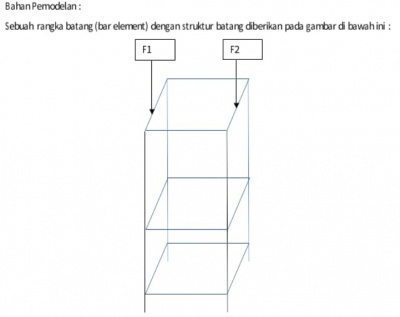
Pada tugas besar kami, diminta mendesign rangka seperti pada gambar tersebut.
Parameter pada rangka batang adalah:
0.6mx0.75mx1.8m (pxlxt)
F1=2000N
F2=1000N
Tugas besar ini memiliki tujuan untuk mengoptimasi pembuatan rangka dengan pemilihan material serta penentuan luas truss. Hal yang kami perhatikan dalam tugas ini adalah: Menentukan material, menentukan luas penampang truss, mencari nilai displacement, reaction, dan streess, menghitung total biaya yang dibutuhkan, melakukan perbandingan dengan material berbeda.
Dalam proses pengoptimalan rangka, terdapat dua metode:
1. Memvariasikan luas dengan material yang sama
2. Luas material truss yang digunakan sama namun material dibedakan
Reaction pada truss
Displacement pada truss
Stress pada truss
Metode material tetap, luas variasi
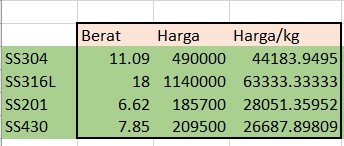
Jenis material merupakan ss201 serta mechanical propertiesnya
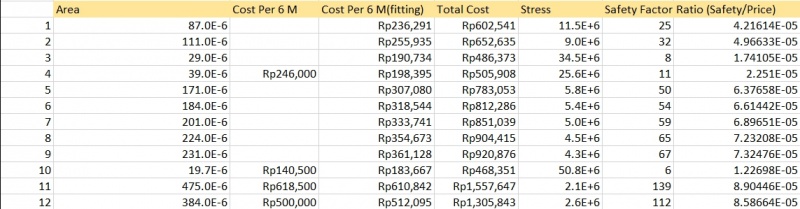
Dengan metode curve fitting didapatkan
Setelah optimasi, mendapatkan hasil :
Metode Luas tetap, material variasi
Data area truss
Variasi material
Perhitungan area locked
Setelah dilakukan proses optimasi didapatkan sebagai berikut
Program open modelica
model TugasBesarMetnum
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=292e6; //Yield Strength (Pa)
parameter Real Area=0.000171; //Area L Profile (Dimension=0.03, Thickness=0,003) (m2)
parameter Real Elas=197e9; //Elasticity SS 201 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[-0.6,0,0,1,1,1;//1
0,0,0,1,1,1;//2
0,0.75,0,1,1,1;//3
-0.6,0.75,0,1,1,1;//4
-0.6,0,0.6,0,0,0;//5
0,0,0.6,0,0,0;//6
0,0.75,0.6,0,0,0;//7
-0.6,0.75,0.6,0,0,0;//8
-0.6,0,1.2,0,0,0;//9
0,0,1.2,0,0,0;//10
0,0.75,1.2,0,0,0;//11
-0.6,0.75,1.2,0,0,0;//12
-0.6,0,1.8,0,0,0;//13
0,0,1.8,0,0,0;//14
0,0.75,1.8,0,0,0;//15
-0.6,0.75,1.8,0,0,0];//16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3]; protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star; end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if; end for;
end TugasBesarMetnum;
Program untuk optimasi
model Opt_Gold
parameter Real[3] y={-514.235, 0.411445, 7.19807E-06};
parameter Real xlo=87.0E-6;
parameter Real xhi=475.0E-6;
parameter Integer N=12; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Curve Fitting
model coba_curve_fitting
parameter Real X[4]={0.000039, 0.00001968, 0.000475, 0.000384};
parameter Real Y[4]={7955, 8000, 7800, 7750};
Real Coe[3];
algorithm
Coe:=Curve_Fitting(X,Y,2);
end coba_curve_fitting;
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B);
end Curve_Fitting;
UAS Metode Numerik
Nomo_1_2.jpg