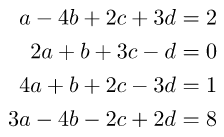John Patrick Anhar
Biodata Diri
Nama : John Patrick Anhar
NPM : 1806201062
TTL : Jakarta, 21 Oktober 2000
Hobi : Berenang
Saya adalah mahasiswa FTUI angkatan 2018 dari jurusan Teknik Mesin dan saya adalah salah satu ciptaan terbaik dari Tuhan Yang Maha Esa, karena pada prinsipnya Tuhan Yang Maha Esa itu mendesain manusia dengan sebaik-baiknya makhluk.
Saya mengikuti kuliah Teknik Mesin karena saya menyukai di bidang otomotif sejak saya kecil dan jurusan ini sungguh berkaitan dengan bidang tersebut. Di jurusan Teknik Mesin ini ada banyak mata kuliah yang saya ikuti, salah satunya yaitu mata kuliah Metode Numerik.
Contents
- 1 Biodata Diri
- 2 Tujuan Mempelajari Metode Numerik
- 3 Metode Numerik
- 3.1 Pertemuan Minggu 1 (11 November 2020)
- 3.2 Pertemuan Minggu 2 (18 November 2020)
- 3.3 Pertemuan Minggu 3 (25 November 2020)
- 3.4 Pertemuan Minggu 4 (2 Desember 2020)
- 3.5 Kelas Pengganti Minggu 5 (14 Desember 2020)
- 3.6 Pertemuan Minggu 6 (16 Desember 2020)
- 3.7 Pertemuan Minggu 7 (23 Desember 2020)
- 3.8 Tugas Besar Metode Numerik
Tujuan Mempelajari Metode Numerik
Tujuan dari mempelajari metode numerik adalah:
- Memahami konsep dasar metode numerik dengan baik.
- Mampu menerapkan konsep metode numerik.
- Mampu menerapkan metode numerik untuk menyelesaikan berbagai persoalan teknik.
- Mendapat nilai tambah/adab agar menjadi manusia yang beradab.
Metode Numerik
Saya telah mengikuti mata kuliah ini selama setengah semester dan saya sudah mempelajari beberapa hal, seperti apa itu penyelesaian matematika menggunakan metode numerik, error-error dalam perhitungan secara numerik, turunan forward centered dan backward, cara-cara melakukan interpolasi dan regresi, serta cara mencari akar dari suatu persamaan secara numerik seperti menggunakan metode Newton-Raphson, metode Bisection, dan metode Secant.
Pertemuan Minggu 1 (11 November 2020)
Pada pertemuan minggu pertama ini, saya belajar bahwa sebagai manusia kita sebaiknya dapat mengetahui apa saja hal-hal yang kita pahami dan tidak kita pahami. Lalu berikutnya saya juga belajar bahwa komputer dapat membantu kita manusia untuk menyelesaikan berbagai persoalan. Namun meskipun teknologi komputer dan pengetahuan manusia saat ini sudah sangat berkembang, manusia dan komputer masih memiliki limitasi tertentu seperti contohnya tidak mampu menentukan nilai 1/0 dimana hanya Tuhan yang tahu nilainya. Oleh karena itu manusia tidak boleh melupakan Tuhan sebab hanya Tuhan yang Maha Tahu.
Tugas Minggu 1
Pada minggu ini, mahasiswa diberikan tugas untuk membuat video mengenai tutorial penggunaan software OpenModelica. Berikut ini video tutorial dasar-dasar penggunaan OpenModelica yang saya buat:
Pertemuan Minggu 2 (18 November 2020)
Pada pertemuan minggu kedua ini, kami diminta memberikan penjelasan mengenai apa yang sudah kami kerjakan pada pertemuan minggu pertama dan apa saja hal-hal yang sudah kami lakukan menggunakan OpenModelica.
Pada pertemuan ini juga kami dijelaskan oleh Pak Dai alasan mengapa aplikasi yang digunakan adalah OpenModelica dan bukan aplikasi lainnya seperti Python. Alasannya adalah karena OpenModelica merupakan aplikasi yang fungsi utamanya adalah modelling dan bukan programming, dimana sebenarnya modelling ini lebih tepat untuk seorang engineer. Simulasi yang dilakukan OpenModelica memang sedikit lebih lama dibandingkan aplikasi lainnya, karena bahasa yang ditulis di OpenModelica akan dikonversi terlebih dahulu kedalam bahasa C++ baru diproses datanya sebab OpenModelica tidak memiliki bahasa pemrograman tersendiri.
Lalu, kami pun diajarkan mengenai jenis-jenis file pada OpenModelica. Pada kesempatan kali ini kami mempelajari mengenai jenis file function dan file class. Contoh fungsi yang kami buat adalah sebagai berikut: FungsiTambahX1.mo
function FungsiTambahX1 input Real X; output Real Y; algorithm Y:=X+10; end FungsiTambahX1;
Lalu, kami juga diajarkan cara untuk memanggil fungsi tersebut ke dalam suatu class, yaitu contohnya seperti berikut ini:
Panggil.mo
class Panggil parameter Real X1=5; Real Hasil10TambahX1; equation Hasil10TambahX1=FungsiTambahX1(X1); end Panggil;
Dalam fungsi 'FungsiTambahX1.mo' input nya adalah sebuah variabel misalnya X dan output dari fungsinya adalah Y yang merupakan hasil penjumlahan X+10. Ketika fungsi ini dipanggil ke class 'Panggil.mo', nilai input fungsi ini diisi dengan nilai X1.
Tugas Minggu 2
Pada minggu ini, mahasiswa diberikan tugas untuk mencoba memanggil suatu fungsi kedalam suatu class seperti yang sudah dicontohkan, namun menggunakan persamaan aljabar simultan dan variable array. Persamaan aljabar simultan merupakan persamaan yang kompleks dimana persamaan ini terdiri dari banyak variabel yang perlu dicari valuenya. Variable array merupakan kumpulan variabel yang disimpan dalam nama yang sama namun tetap memiliki nilai yang berbeda-beda.
Untuk itu, pada tugas ini saya akan mencoba menyelesaikan 4 persamaan dengan 4 variabel yang akan dicari nilai dari masing-masing variabel tersebut. Contoh yang saya ambil ialah sebagai berikut:
Untuk menjawab persoalan tersebut pertama-tama saya membuat fungsi Gauss seperti berikut ini: FungsiGauss.mo
function FungsiGauss input Real U[4,4]; input Real V[4]; output Real O[4]; algorithm W:=Modelica.Math.Matrices.solve(U,V); end FungsiGauss;
Fungsi tersebut saya panggil kedalam class berikut ini: ClassGauss.mo
class ClassGauss
parameter Real A[4,4]=[1,-4,2,3;2,1,3,-1;4,1,2,-3;3,-4,-2,2];
parameter Real B[4]={2,0,1,8};
Real O[4];
equation
O=FungsiGauss(A,B);
end ClassGauss;
Berikut video penjelasan yang saya buat:
Pertemuan Minggu 3 (25 November 2020)
Pada pertemuan kali ini, saya mempelajari banyak hal baru. Salah satunya yaitu belajar tentang cara membuat fungsi sendiri tanpa menggunakan fitur yang disediakan oleh OpenModelica. Pada kesempatan ini saya diberikan penjelasan oleh beberapa teman saya yaitu Josiah Enrico dan Christopher Salendu Erwin mengenai fungsi array dengan menggunakan metode Newton Raphson dan juga cara membuat fungsi Gauss Jordan di OpenModelica dengan sangat jelas. Pseudocode fungsi yang dijelaskan oleh Christopher adalah sebagai berikut: GaussJordan.mo
function GaussJordan
input Real [:,:] A; //matrix yang ingin di OBE
output Real [:,:] B; //matrix yang sudah diproses OBE
protected // untuk local variable
Integer h = 1; //pivot row
Integer k = 1; //pivot column
Integer m = size(A,1); //Number of row
Integer n = size(A,2); //Number of column
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
//input A ke matrix B
B := A;
//dealing with error
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Mencari pivot
pivot_column:= {B[i,h] for i in h:m};
//Mencari baris terbawah yang mempunyai nilai pivot terbesar
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
if B[max_row,k] == 0 then
k:=k+1;
else
//tukar row h dengan max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//bagi pivot row dengan pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//pindah ke pivot column dan row selanjutnya
h := h+1;
k := k+1;
end if;
end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//mencari pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// jika tidak ada pivot, maka pindah ke row berikutnya
if B[h,k] == 0 then
h:= h-1;
else
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//pindah ke pivot row dan column berikutnya
h:=h+1;
k:=k+1;
end if;
end while;
end GaussJordan;
Tugas Minggu 3
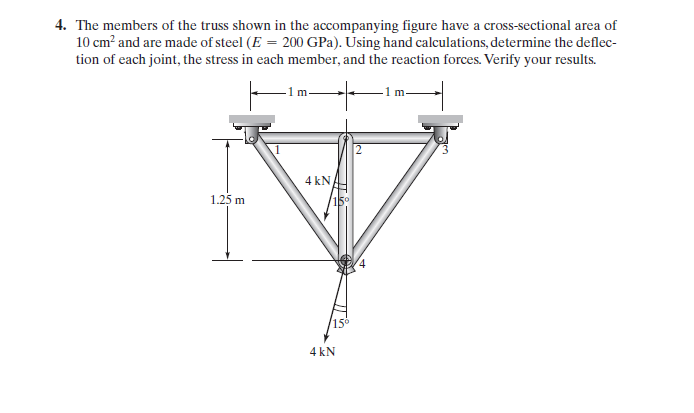
Pada pertemuan minggu ini juga kami diberikan tugas untuk membuat program sederhana menggunakan OpenModelica untuk menyelesaikan suatu kasus terkait struktur seperti pada gambar berikut:
Maka, saya membuatnya menggunakan cara seperti yang dicontohkan di buku untuk example 3.1 dan pseudocodenya seperti ini: Truss.mo
class Truss
parameter Real E=200e9;
parameter Real A=0.001;
Real L1=1;
Real L2=1;
Real L3=1.6;
Real L4=1.25;
Real L5=1.6;
Real tetha1=DEGtoRAD(0); //DEGtoRAD untuk mengubah satuan sudut
Real tetha2=DEGtoRAD(0);
Real tetha3=DEGtoRAD(231.34);
Real tetha4=DEGtoRAD(270);
Real tetha5=DEGtoRAD(308.66);
Real U[8]; //Displacement
Real R[8]; //Reaction
//Hitung K masing-masing Truss
//Truss1
Real [8,8] K1 = (E*A/L1)*
[(cos(tetha1))^2,(cos(tetha1)*sin(tetha1)),-(cos(tetha1))^2,-(cos(tetha1)*sin(tetha1)),0,0,0,0;
(cos(tetha1)*sin(tetha1)),(sin(tetha1))^2,-(cos(tetha1)*sin(tetha1)),-(sin(tetha1))^2,0,0,0,0;
-(cos(tetha1))^2,-(cos(tetha1)*sin(tetha1)),(cos(tetha1))^2,(cos(tetha1)*sin(tetha1)),0,0,0,0;
-(cos(tetha1)*sin(tetha1)),-(sin(tetha1))^2,(cos(tetha1)*sin(tetha1)),(sin(tetha1))^2,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0];
//Truss2
Real [8,8] K2 = (E*A/L2)*
[0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,(cos(tetha2))^2,(cos(tetha2)*sin(tetha2)),-(cos(tetha2))^2,-(cos(tetha2)*sin(tetha2)),0,0;
0,0,(cos(tetha2)*sin(tetha2)),(sin(tetha2))^2,-(cos(tetha2)*sin(tetha2)),-(sin(tetha2))^2,0,0;
0,0,-(cos(tetha2))^2,-(cos(tetha2)*sin(tetha2)),(cos(tetha2))^2,(cos(tetha2)*sin(tetha2)),0,0;
0,0,-(cos(tetha2)*sin(tetha2)),-(sin(tetha2))^2,(cos(tetha2)*sin(tetha2)),(sin(tetha2))^2,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0];
//Truss3
Real [8,8] K3 = (E*A/L3)*
[0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,(cos(tetha3))^2,(cos(tetha3)*sin(tetha3)),-(cos(tetha3))^2,-(cos(tetha3)*sin(tetha3));
0,0,0,0,(cos(tetha3)*sin(tetha3)),(sin(tetha3))^2,-(cos(tetha3)*sin(tetha3)),-(sin(tetha3))^2;
0,0,0,0,-(cos(tetha3))^2,-(cos(tetha3)*sin(tetha3)),(cos(tetha3))^2,(cos(tetha3)*sin(tetha3));
0,0,0,0,-(cos(tetha3)*sin(tetha3)),-(sin(tetha3))^2,(cos(tetha3)*sin(tetha3)),(sin(tetha3))^2];
//Truss4
Real [8,8] K4 = (E*A/L4)*
[0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,(cos(tetha4))^2,(cos(tetha4)*sin(tetha4)),0,0,-(cos(tetha4))^2,-(cos(tetha4)*sin(tetha4));
0,0,(cos(tetha4)*sin(tetha4)),(sin(tetha4))^2,0,0,-(cos(tetha4)*sin(tetha4)),-(sin(tetha4))^2;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,-(cos(tetha4))^2,-(cos(tetha4)*sin(tetha4)),0,0,(cos(tetha4))^2,(cos(tetha4)*sin(tetha4));
0,0,-(cos(tetha4)*sin(tetha4)),-(sin(tetha4))^2,0,0,(cos(tetha4)*sin(tetha4)),(sin(tetha4))^2];
//Truss5
Real [8,8] K5 = (E*A/L5)*
[(cos(tetha5))^2,(cos(tetha5)*sin(tetha5)),0,0,0,0,-(cos(tetha5))^2,-(cos(tetha5)*sin(tetha5));
(cos(tetha5)*sin(tetha5)),(sin(tetha5))^2,0,0,0,0,-(cos(tetha5)*sin(tetha5)),-(sin(tetha5))^2;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0;
-(cos(tetha5))^2,-(cos(tetha5)*sin(tetha5)),0,0,0,0,(cos(tetha5))^2,(cos(tetha5)*sin(tetha5));
-(cos(tetha5)*sin(tetha5)),-(sin(tetha5))^2,0,0,0,0,(cos(tetha5)*sin(tetha5)),(sin(tetha5))^2];
//Buat ke KGlobal
Real KGlobal [8,8] = K1+K2+K3+K4+K5;
//Masukkan Boundary Condition
Real KGlobalBoundary [8,8]=
[10^6,0,0,0,0,0,0,0;
0,10^6,0,0,0,0,0,0;
-2e7,0,4e7,38223.5,-2e7,0,-91.3155,-38223.5;
0,0,38223.5,1.5e7,0,0,-38223.5,-1e7;
0,0,0,0,10^6,0,0,0;
0,0,0,0,0,10^6,0,0;
-4e6,-6e6,-91.3155,-38223.5,-4e6,-6e6,9.7e6,51373.2;
6e6,-7e6,-38223.5,-1e7,-6e6,-7e6,51373.2,3.1e7];
//Karena 1 dan 3 static maka F1x,F1y,F3x,F3y = 0
//F2x=F*sin15
//F2y=F*cos15
//F4x=F*sin15
//F4y=F*cos15
Real F[8] = {0,0,-1035.276,3865.703,0,0,-1035.276,3863.703};
equation
U=FungsiGaussJordan(KGlobalBoundary,F);
R=KGlobal*U-F;
end Truss;
Pseudocode fungsi DEGtoRAD: DEGtoRAD.mo
function DEGtoRAD input Real deg; output Real rad; protected constant Real pi = 3.14; algorithm rad:=deg*pi/180; end DEGtoRAD;
Kemudian kami juga diminta untuk membuat pseudocode dari Fig. 9.4 di buku: NaiveGauss.mo
function NaiveGauss
input Real [3,3] A;
input Real [3] B;
output Real [3] x;
protected
Real [3,3] a;
Real [3] b;
Integer m = size(A,1); // kolom
Integer n = size(A,2); // baris
Real k = 1;
Real i = 1;
Real j = 1;
Real factor = 1;
Real sum = 1;
algorithm
// Transfer input matrix (A,B) into variables (a,b)
a := A;
b := B;
// Forward Elimination
for k in 1:(n-1) loop
for i in (k+1):n loop
factor := a[i,k] / a[k,k];
for j in (k+1):n loop
a[i,j] := a[i,j] - (factor * a[k,j]);
end for;
b[i] := b[i] - (factor * b[k]);
end for;
end for;
// Back Substitution
x[n] := b[n] / a[n,n];
for i in (n-1):(-1) loop
sum := b[i];
for j in (i+1):n loop
sum := sum - (a[i,j] * x[j]);
end for;
x[i] := sum / a[i,i];
end for;
end NaiveGauss;
Lalu digunakan untuk menyelesaikan example 9.5
Ex95.mo
class Ex95
parameter Real A[3,3]=[3,-0.1,-0.2;
0.1,7,-0.3;
0.3,-0.2,10];
parameter Real B[3]={7.85,-19.3,71.4};
Real x[3];
equation
x=NaiveGauss(A,B);
end Ex95;
Pertemuan Minggu 4 (2 Desember 2020)
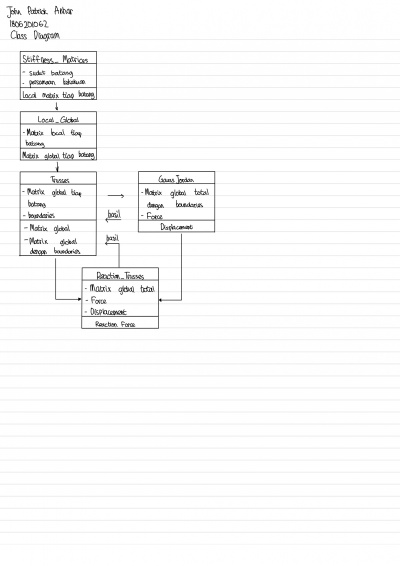
Pada pertemuan kali ini, saya diberikan kuis oleh Pak DAI untuk membuat class diagram & flowchart setiap class untuk coding yang dibuat oleh Josiah Enrico.
Kuis Diagram Class dan Flowchart
Tugas Minggu 4
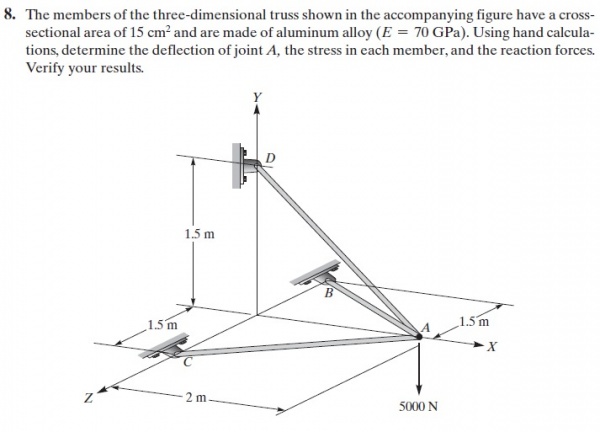
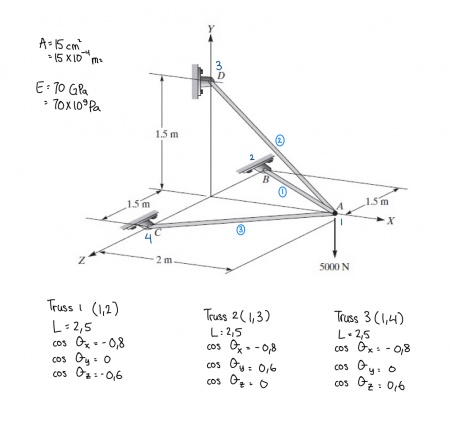
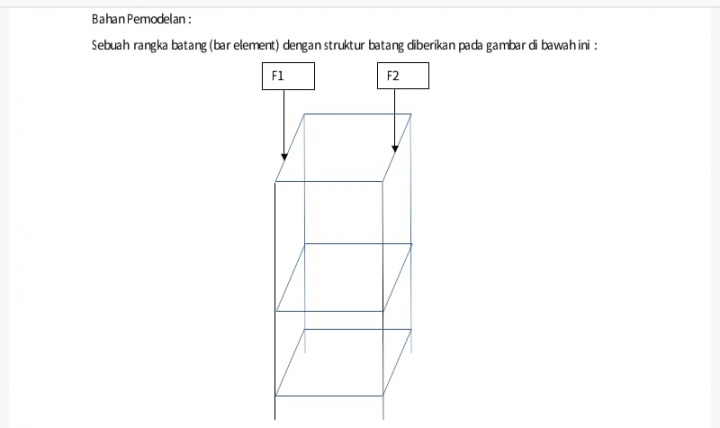
Pada pertemuan minggu ini, saya diberikan tugas oleh Pak DAI untuk mengerjakan soal berikut:
Berikut Free Body Diagram yang saya buat:
Matriks ditulis dengan urutan sebagai berikut
Inisiasi : [{Truss} , {Node1} , {Node2} , {CosX} , {CosY} , {CosZ} , {A} , {E} , {L}]
Load : [{Node} , {Fx} , {Fy} , {Fz}]
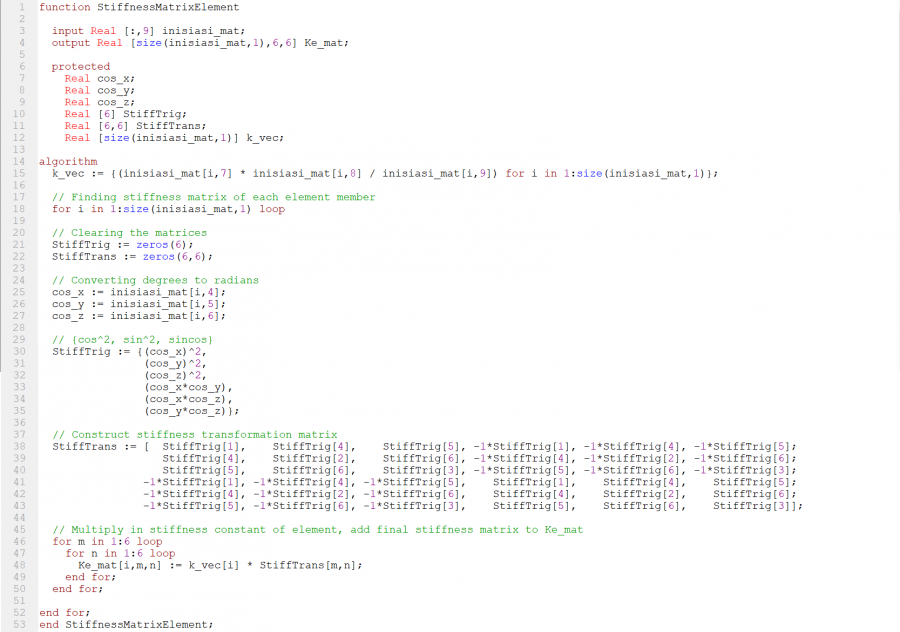
Langkah pertama yaitu membuat Stiffness Matrix Element (per truss) seperti berikut:
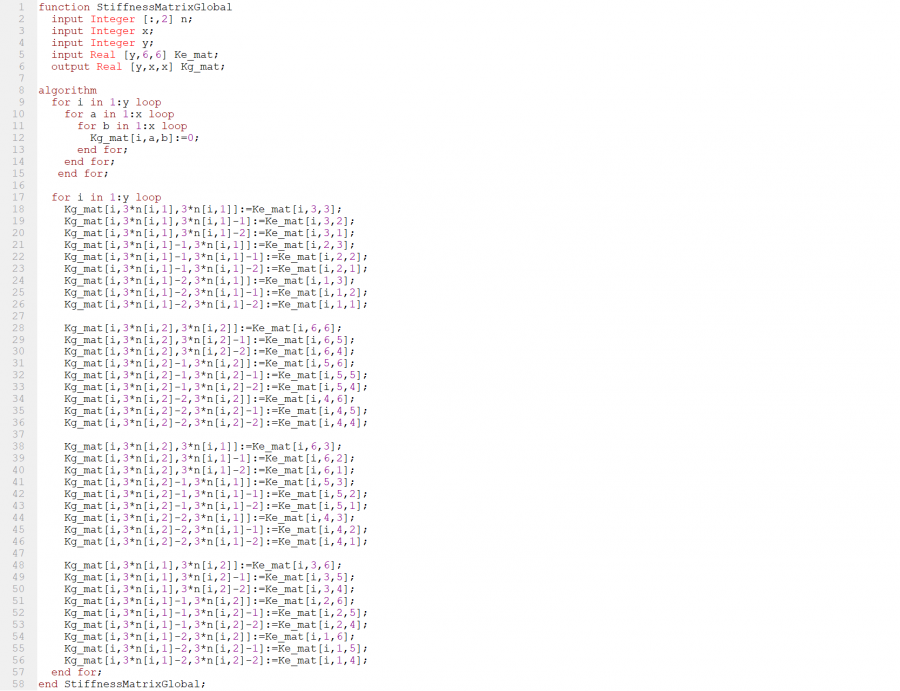
Berikutnya, dari matriks tersebut dibuat Stiffness Matrix Global berukuran 12x12 seperti berikut:
Lalu langkah berikutnya yaitu menjumlahkan matriks global dari masing-masing elemen
Selanjutnya menentukan boundaries
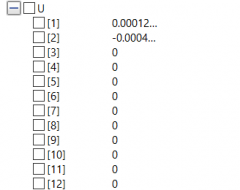
Lalu, mencari nilai displacement (U) menggunakan fungsi Gauss-Jordan
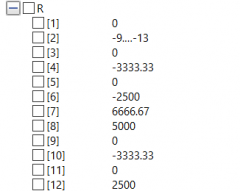
Selanjutnya untuk mencari nilai gaya reaksinya (R) digunakan fungsi berikut
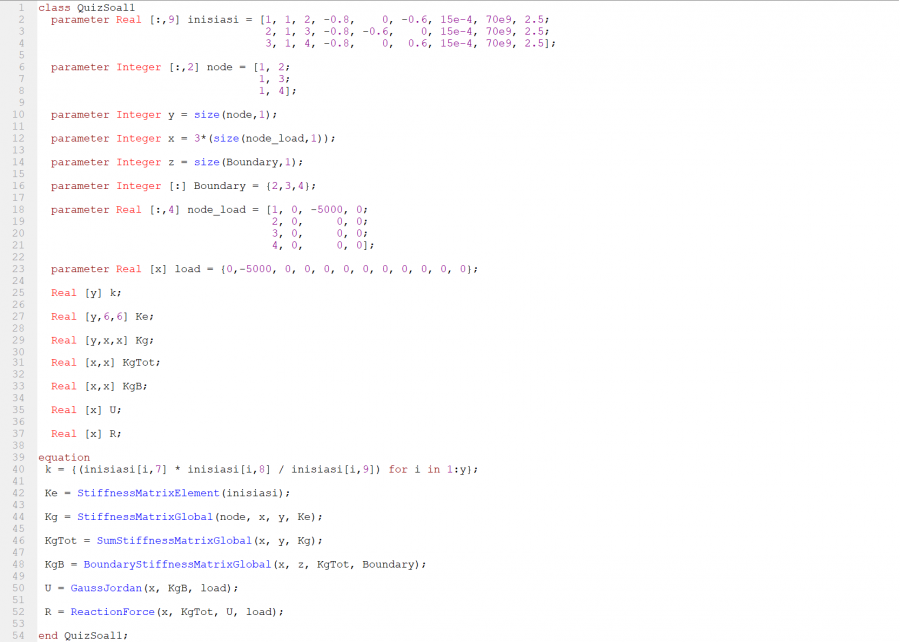
Lalu dibuat class yang memproses semua fungsi
Setelah di simulate, diperoleh nilai displacement (U) dan gaya reaksi (R) sebagai berikut:
Berikut video penjelasan saya mengenai penyelesaian soal diatas:
Kelas Pengganti Minggu 5 (14 Desember 2020)
Kelas Metode Numerik seharusnya diadakan pada hari Rabu setiap minggunya. Namun, pada tanggal 9 Desember 2020 diadakan Pemilihan Kepala Daerah di seluruh Indonesia sehingga dijadikan hari libur nasional. Oleh karena itu pada pertemuan minggu ke 5 ini, diadakan kelas pengganti pada tanggal 23 Desember 2020. Pada minggu ini kami diminta untuk melakukan muhasabah dan melakukan penilaian terhadap kemampuan kami masing-masing mengenai pemahaman kami dalam aplikasi Metode Numerik secara sejujurnya. Kemudian kami juga diminta untuk menjelaskan pemahaman kami tersebut. Lalu, di akhir kelas ini juga kami diberikan tugas besar.
Pertemuan Minggu 6 (16 Desember 2020)
Aplikasi metode numerik dalam kasus optimasi
Pada hari ini kami akan mempelajari mengenai optimasi dengan menggunakan metode numerik. Optimasi adalah teknik untuk memperoleh nilai optimum dari suatu sistem. Topik optimasi kali ini akan dibawakan oleh Bu Candra. Metode optimasi yang digunakan adalah metode Golden Ratio Method. Pseudocodenya sebagai berikut:
FungsiObjek.mo
function FungsiObjek import Modelica.Math; input Real x; output Real y; algorithm y:= 2*Math.sin(x)-x^2/10; end FungsiObjek;
Setelah membuat fungsi objek tersebut, kemudian akan dipanggil kedalam model seperti berikut ini: Golden_Ratio.mo
model Golden_Ratio
parameter Integer n = 8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
Real d;
algorithm
xup := 4;
xlow := 0;
for i in 1:n loop
d:=((5^(1/2)-1)/2) * (xup-xlow);
x1[i] := xlow+d;
x2[i] := xup-d;
f1[i] := FungsiObjek(x1[i]);
f2[i] := FungsiObjek(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow := x2[i];
xopt := xup;
yopt := f1[i];
else
xlow :=xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end Golden_Ratio;
Pertemuan Minggu 7 (23 Desember 2020)
Pada pertemuan ini, diadakan kuis dimana kami diminta untuk menghitung defleksi yang dialami sistem yang menjadi tugas besar kami. Untuk menghitung defleksi ini, kami diminta untuk menyelesaikannya dengan menggunakan program yang sudah kami buat. Berikut ini adalah pseudocode yang sudah saya buat:
Kuis2MetNum.mo
class Kuis2MetNum
//Urutan Penulisan: [Truss, Node 1, Node 2, Cx, Cy, Cz, A, E, L]
parameter Real [:,9] inisiasi = [ 1, 1, 2, 0, 1, 0, 9e-4, 190e9, 0.75;
2, 2, 3, 1, 0, 0, 9e-4, 190e9, 0.6;
3, 3, 4, 0, -1, 0, 9e-4, 190e9, 0.75;
4, 1, 4, 1, 0, 0, 9e-4, 190e9, 0.6;
5, 5, 6, 0, 1, 0, 9e-4, 190e9, 0.75;
6, 6, 7, 1, 0, 0, 9e-4, 190e9, 0.6;
7, 7, 8, 0, -1, 0, 9e-4, 190e9, 0.75;
8, 5, 8, 1, 0, 0, 9e-4, 190e9, 0.6;
9, 9, 10, 0, 1, 0, 9e-4, 190e9, 0.75;
10, 10, 11, 1, 0, 0, 9e-4, 190e9, 0.6;
11, 11, 12, 0, -1, 0, 9e-4, 190e9, 0.75;
12, 9, 12, 1, 0, 0, 9e-4, 190e9, 0.6;
13, 1, 5, 0, 0, 1, 9e-4, 190e9, 0.75;
14, 2, 6, 0, 0, 1, 9e-4, 190e9, 0.75;
15, 3, 7, 0, 0, 1, 9e-4, 190e9, 0.75;
16, 4, 8, 0, 0, 1, 9e-4, 190e9, 0.75;
17, 5, 9, 0, 0, 1, 9e-4, 190e9, 0.75;
18, 6, 10, 0, 0, 1, 9e-4, 190e9, 0.75;
19, 7, 11, 0, 0, 1, 9e-4, 190e9, 0.75;
20, 8, 12, 0, 0, 1, 9e-4, 190e9, 0.75;
21, 9, 13, 0, 0, 1, 9e-4, 190e9, 0.3;
22, 10, 14, 0, 0, 1, 9e-4, 190e9, 0.3;
23, 11, 15, 0, 0, 1, 9e-4, 190e9, 0.3;
24, 12, 16, 0, 0, 1, 9e-4, 190e9, 0.3];
parameter Integer [:,2] node = [ 1, 2;
2, 3;
3, 4;
1, 4;
5, 6;
6, 7;
7, 8;
5, 8;
9, 10;
10, 11;
11, 12;
9, 12;
1, 5;
2, 6;
3, 7;
4, 8;
5, 9;
6, 10;
7, 11;
8, 12;
9, 13;
10, 14;
11, 15;
12, 16];
parameter Integer y = size(node,1);
parameter Integer x = 3*(size(node_load,1));
parameter Integer z = size(Boundary,1);
parameter Integer [:] Boundary = {13,14,15,16};
parameter Real [:,4] node_load = [ 1, 0, 1000, 0;
2, 0, 1000, 0;
3, 0, 500, 0;
4, 0, 500, 0;
5, 0, 0, 0;
6, 0, 0, 0;
7, 0, 0, 0;
8, 0, 0, 0;
9, 0, 0, 0;
10, 0, 0, 0;
11, 0, 0, 0;
12, 0, 0, 0;
13, 0, 0, 0;
14, 0, 0, 0;
15, 0, 0, 0;
16, 0, 0, 0];
parameter Real [x] load = {0, 1000, 0,
0, 1000, 0,
0, 500, 0,
0, 500, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0,
0, 0, 0};
Real [y] k;
Real [y,6,6] Ke;
Real [y,x,x] Kg;
Real [x,x] KgTot;
Real [x,x] KgB;
Real [x] U;
Real [x] R;
equation
k = {(inisiasi[i,7] * inisiasi[i,8] / inisiasi[i,9]) for i in 1:y};
Ke = MatriksKekakuanElemen(inisiasi);
Kg = MatriksKekakuanGlobal(node, x, y, Ke);
KgTot = MatriksTotalKekakuanGlobal(x, y, Kg);
KgB = MatriksKekakuanGlobalDenganBoundary(x, z, KgTot, Boundary);
U = FungsiGaussJordan(x, KgB, load);
R = FungsiReactionForce(x, KgTot, U, load);
end Kuis2MetNum;
Tugas Besar Metode Numerik
Latar Belakang
Optimasi merupakan suatu langkah yang dilakukan untuk mendapatkan nilai optimum. Dalam proses desain suatu objek, optimasi memegang peranan yang penting sebab dengan melakukan optimasi maka dapat diperoleh kualitas yang baik dengan harga yang serendah-rendahnya.
Tujuan
Memperoleh desain struktur truss terbaik dalam artian diperoleh harga yang serendah-rendahnya dengan kemampuan menahan beban yang sesuai dengan target.
Rangka yang dianalisis dalam tugas besar adalah sebagai berikut:
Dan berikut adalah keterangannya:
Asumsi
-Truss yang bersentuhan dengan lantai fixed
-Lokasi beban F1 dan F2 berada di tengah dari truss sehingga beban terbagi menjadi dua pada sudutnya
-Tidak terjadi bending
Metodologi Pengerjaan
Untuk mengerjakan tugas besar ini, akan digunakan coding untuk dapat mengoptimasi material yang dapat menahan beban dengan baik (memiliki kekuatan tinggi dan safety factor yang baik dalam menahan beban yang diberikan) namun dengan harga yang paling baik.
Ada 2 metode yang digunakan untuk melakukan optimasi ini:
1. Menentukan jenis material yang digunakan terlebih dahulu dan kemudian melakukan perhitungan terhadap harga, safety factor, dan rasio perbandingan safety factor dengan harga dengan memvariasikan cross-sectional area yang berbeda-beda.
2. Menentukan cross-sectional area besi siku terlebih dahulu dan kemudian melakukan perhitungan terhadap harga, safety factor, dan rasio perbandingan safety factor dengan harga dengan memvariasikan material yang berbeda-beda.
Perhitungan
1. Elasticity Locked
Dalam perhitungan ini material yang saya tentukan terlebih dahulu adalah Stainless Steel SS316L yang propertiesnya sebagai berikut:
Material : Stainless Steel SS316L Yield Strength : 290 MPa Modulus of Elasticity : 193 GPa
Kemudian dilakukan perhitungan dengan menggunakan Excel sehingga diperoleh data sebagai berikut:
Untuk harga besi siku yang digunakan saya mengambil referensi harga dari http://aspdistributor.blogspot.com/2016/11/harga-stainless-steel-siku-ss304.html.
Lalu selanjutnya dilakukan optimasi dan hasilnya adalah sebagai berikut:
2. Area Locked
Dalam perhitungan ini cross-sectional area yang saya tentukan terlebih dahulu luasnya adalah 0,000171m² yang merupakan luas penampang dari besi siku dengan dimensi 30x30mm dengan ketebalan 3mm.
Kemudian dilakukan perhitungan dengan menggunakan Excel sehingga diperoleh data sebagai berikut:
Lalu selanjutnya dilakukan optimasi dan hasilnya adalah sebagai berikut: