Alvi Arya Ramadhan
Contents
Biodata
assalamualaikum Wr.Wb
Nama : Alvi Arya Ramadhan
NPM : 1806201434
Tempat, tanggal lahir : Jakarta, 3 Desember 2000
Jurusan : Teknik Mesin
Angkatan : 2018
Saya adalah mahasiswa Semester 5 jurusan teknik mesin FTUI angkatan 2018. Pada semester ini saya mengambil mata kuliah metode numerik untuk menambah kapasitas dalam diri saya dan memenuhi syarat perkuliahan. saya mengambil jurusan ini karena tertarik dengan bidang mekanika serta konversi energi yang akan banyak digunakan dalam industri 4.0 nantinya dan Berharap saya menjadi pribadi yang lebih baik lagi sehingga dapat berguna bagi lingkungan dengan ilmu yang ada dalam diri saya, saya suka olahraga karena menurut saya itu memiliki manfaat dalam jangka panjang baik jasmani dan rohani.
Tujuan dari mata kuliah metode numerik ini antara lain adalah sebagai berikut,
- Memahami konsep dan prinsip dasar dalam Metode Numerik
- Dapat menerapkan pemahaman dari konsep yang ada di dalam permodelan numerik
- Mampu menerapkan Metode Numerik dalam persoalan engineering
- Mendapat nilai tambah terhadap diri pribadi
Materi Sebelum Uts
sebelumnya saya telah diajarkan beberapa materi sebelum UTS diantaranya:
- penghitungan deret Taylor dan McLaurin dengan metode forward, center, dan backward;
- menghitung persamaan dengan metode Bisection, Secant,dan Raphson;
- mencari nilai interpolasi dan regresi linier menggunakan matriks.
Tugas 1
- mempelajari mengenai open modelica
- hasil belajar
Pertemuan (18/11/2020)
Hari ini kita diberi tahu bahwa orang yang yang lebih baik dari hari kemarin adalah orang yang beruntung karena memiliki grafik kehidupan yang meningkat sedangkan orang yang sama saja atau bahkan lebih buruk dari hari kemarin adalah orang yang merugi sebab grafiknya akan menurun. Setelah itu kami diajarkan cara untuk membuat Class panggil dan fungsi untuk membuat sebuah persamaan yang kita rancang sendiri .
Tugas 2
aplikasi modelica dengan class dan funtion dalam permasalahan matriks dengan variabel array
Pertemuan (25/11/2020)
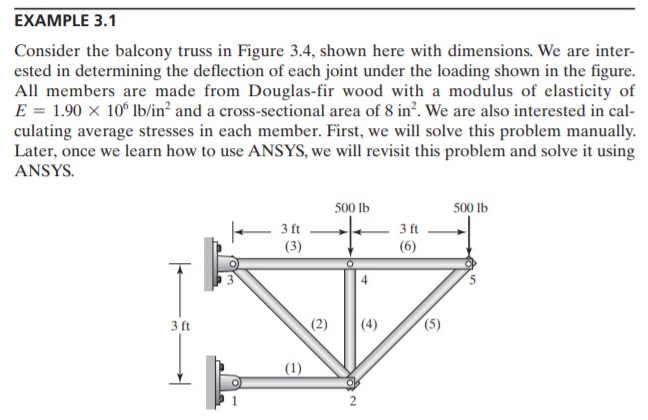
Dijelaskan mengenai Aplikasi Numerik dalam permasalahan Teknik. metode numerik yang sering digunakan untuk melakukan analisa masalah teknik adalah Computation Fluid Dynamics (CFD), Finite Element Analysis (FEA), dan Metode Stokastik. CFD dan FEA berdasarkan hukum-hukum fisika, sementara metode stokastik berbasis data dan statistik. ada beberapa langkah yang harus dilakukan untuk menyelesaikan sebuah masalah teknik, kita harus membuat analisa masalah selanjutnya melakukan permodelan matematis lanjut ke model numerik dan jika sudah mendapatkannya dipindahkan ke komputer sehingga mendapatkan sebuah output berupa solusi permasalahan yang ada.
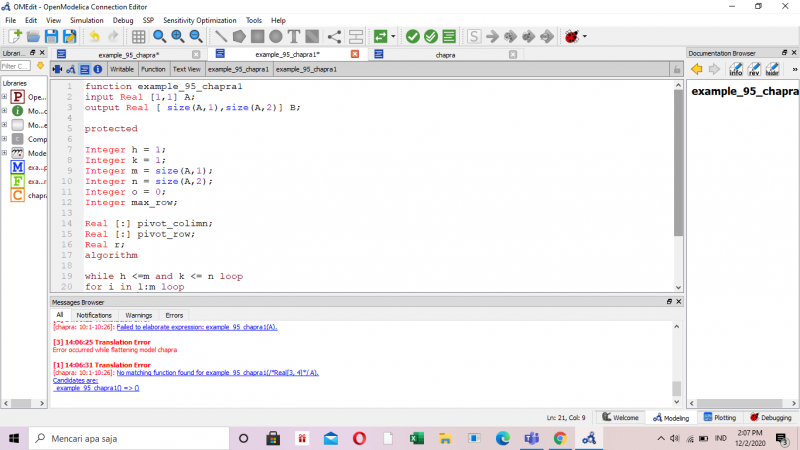
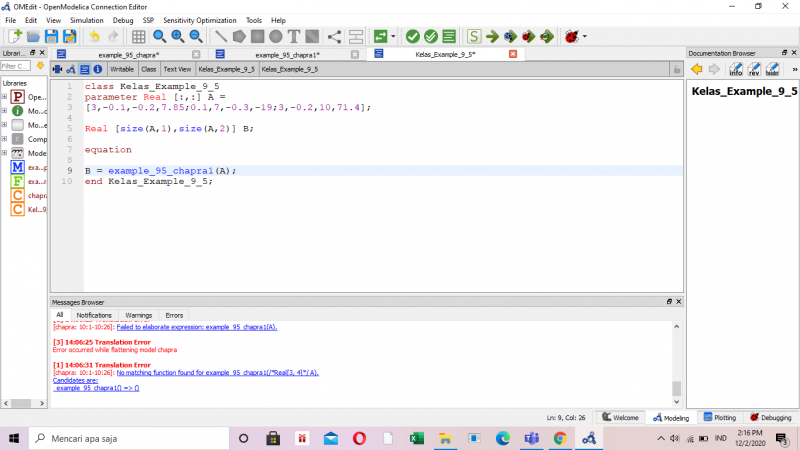
setelah itu beberapa teman kami menampilkan sesuatu yang telah dia pelajari dan kami semua menyimaknya dengan seksama dalam menyelesaikan sistem persamaan dengan membuat fungsi penyelesaian dengan referensi pseudocode 9.4 untuk soal 9.5 dari buku Numerical Methods for Engineers 7th Edition oleh Chapra.
GaussJordan.mo
function GaussJordan input Real [:,:] A; output Real [:,:] B; protected // untuk local variable Integer h = 1; //pivot row Integer k = 1; //pivot coloumn Integer m = size(A,1); //Number of row Integer n = size(A,2); //Number of column Integer c = 0; Integer max_row; // Row index of max number in pivot column Real [:] pivot_column; Real [:] pivot_row; Real [:,:] temp_array; Real r; Real float_error = 10e-10;
algorithm
//fungsi input A dan output B
B := A;
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Finding pivot
pivot_column:= {B[i,h] for i in h:m};
//Mencari baris terbawah yang mempunyai nilai pivot tertinggi
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
if B[max_row,k] == 0 then
k:=k+1;
else
// tukar row h - max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//devide pivot row by pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//move ke pivot kolom dan row selanjutnya
h := h+1;
k := k+1;
end if;
end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//finding pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// no pivot in this row, move to next row
if B[h,k] == 0 then
h:= h-1;
else
//perform row operatation
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//move to next pivot row dan column
h:=h+1;
k:=k+1;
end if;
end while;
end GaussJordan;
dengan hasil
|
Persamaan model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
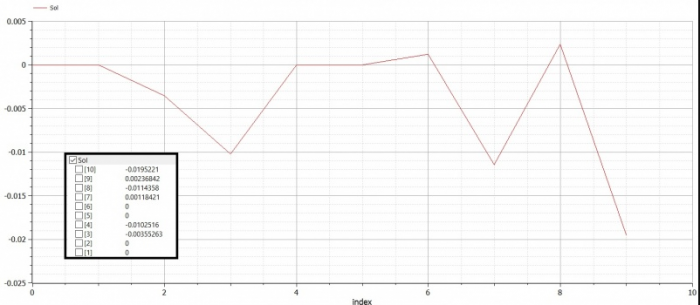
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
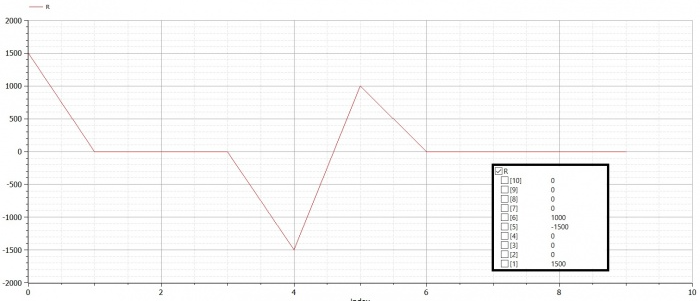
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses;
|
Tugas 3
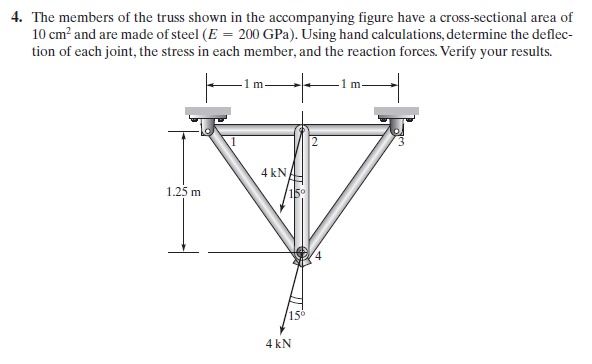
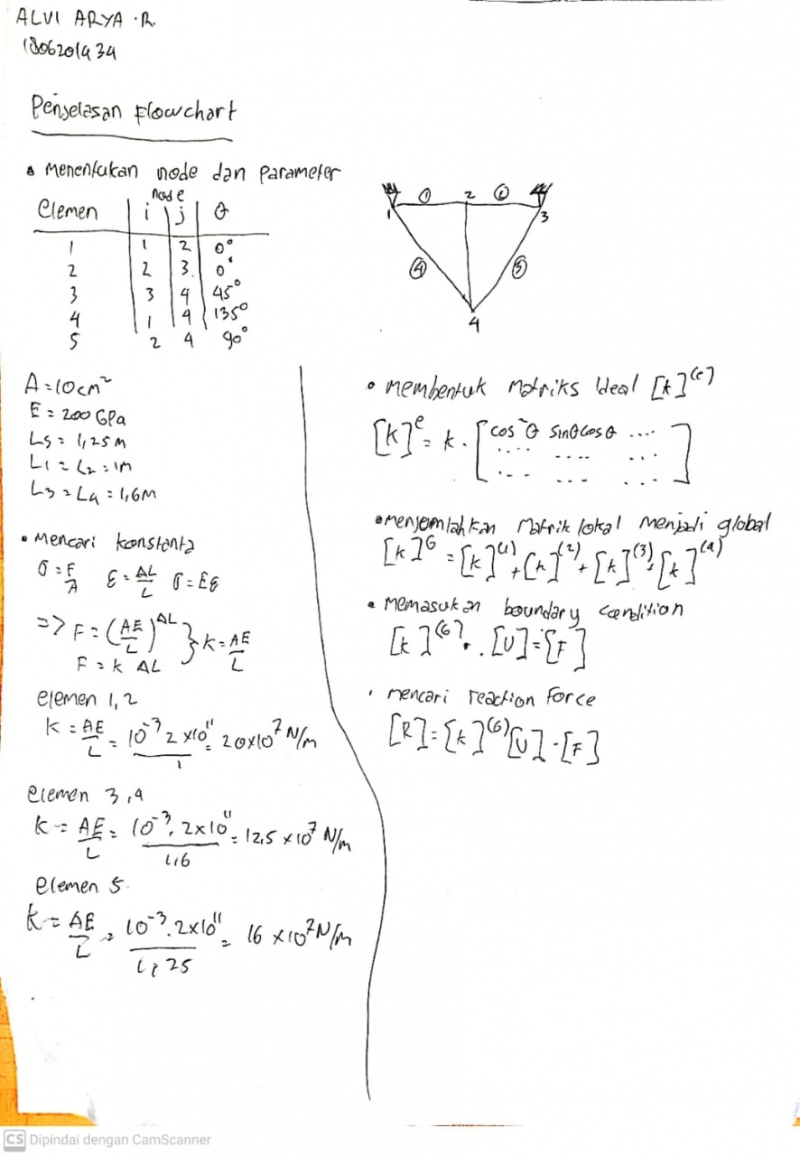
kami diminta untuk menyederhanakan persamaan dari masalah teknik berikut.
|
Persamaan class Trusses_HW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
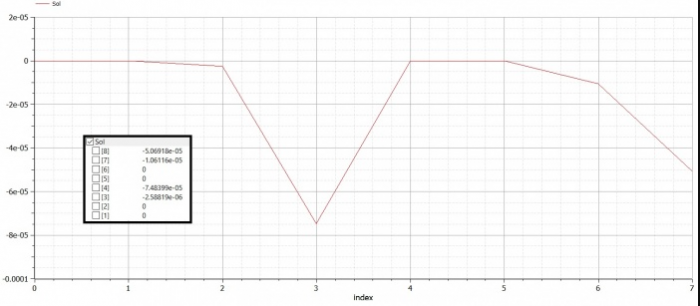
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_HW;
|
Fungsi Panggil
|
Matrice Transformation function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan;
Reaction Matrice Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; |
pertemuan [12-2-2020]
QUIZ FLOWCHART DAN KELAS DIMENSI
Tugas 4
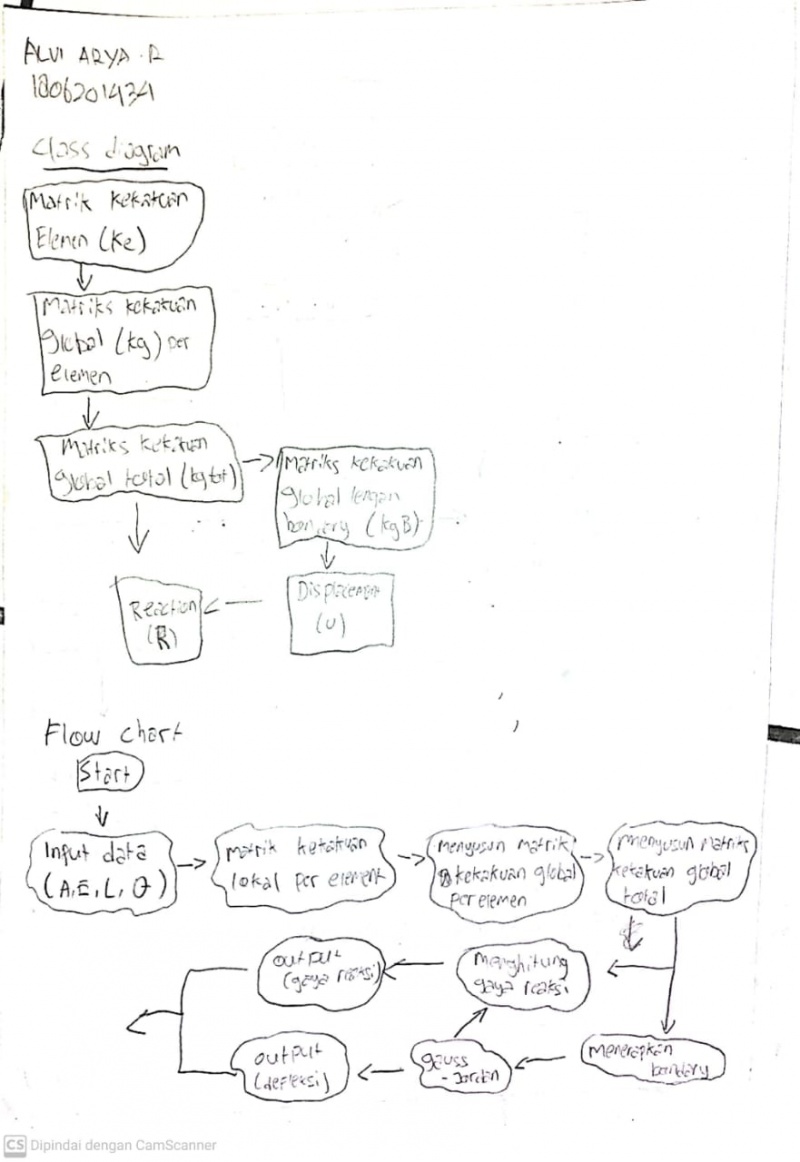
Mebuat flow chart diagram class dan coding open modelica
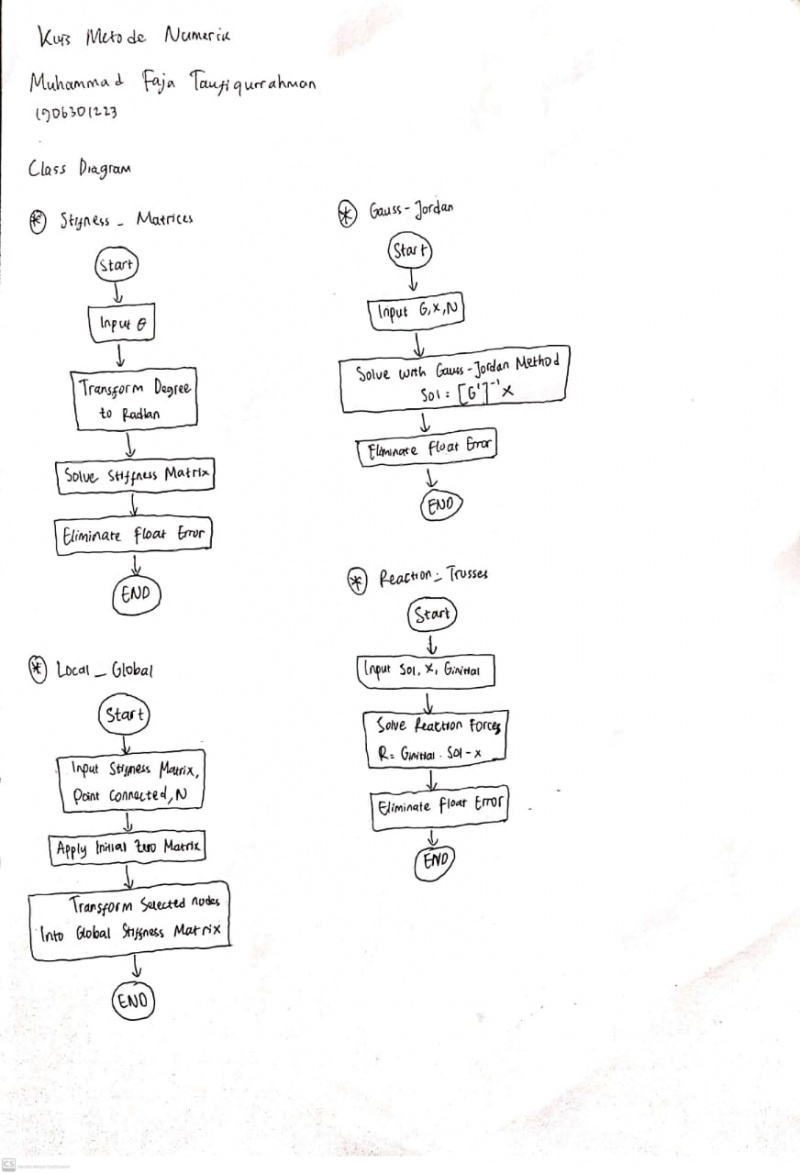
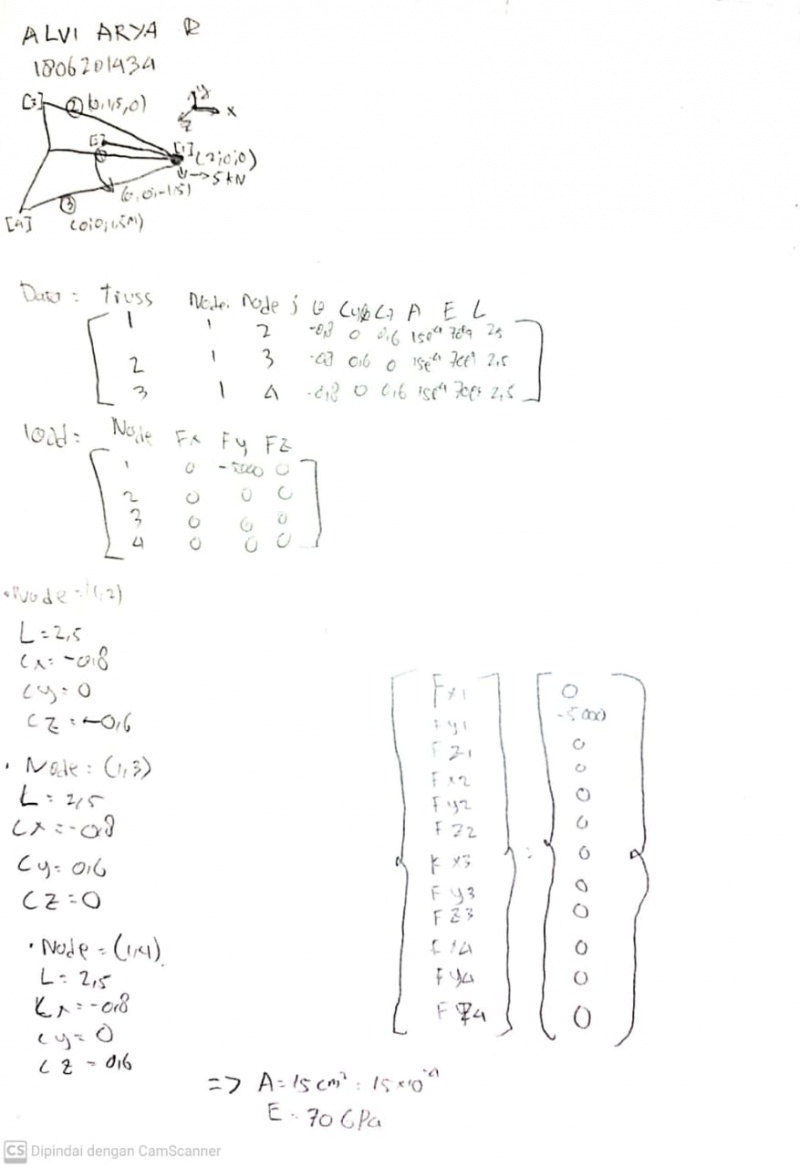
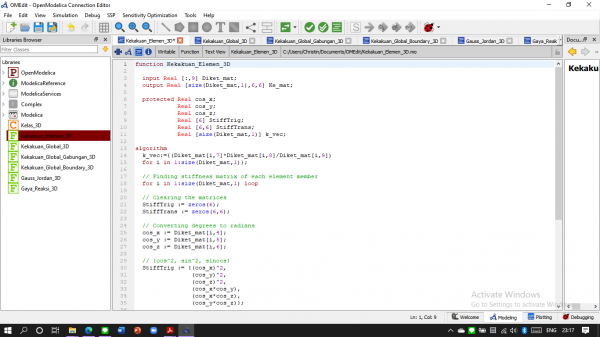
Dibawah ini adalah coding untuk soal 3d trusses berdasarkan dari saudara Ahmad Mohammad Fahmi dari kelas metode numerik 03 :
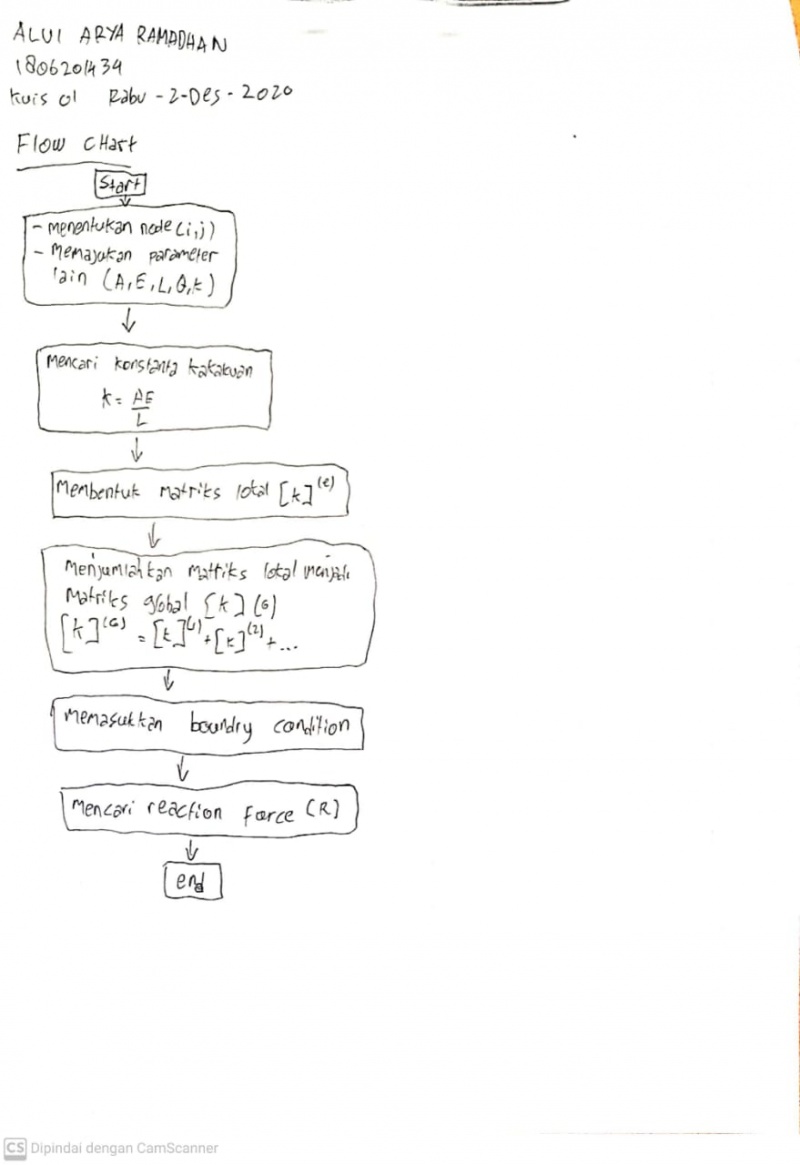
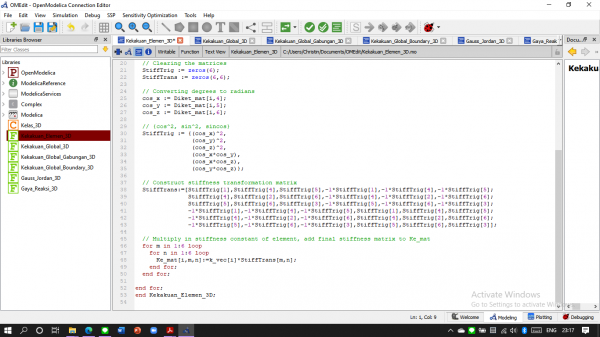
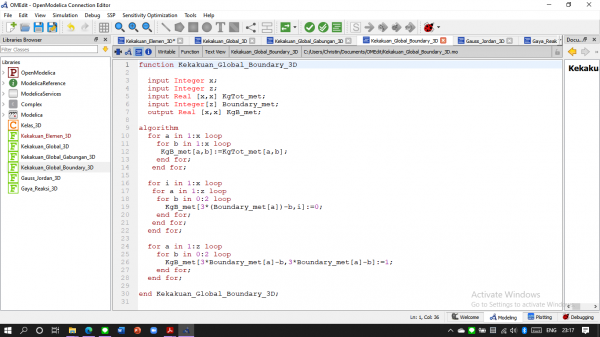
Membuat Kekakuan elemen
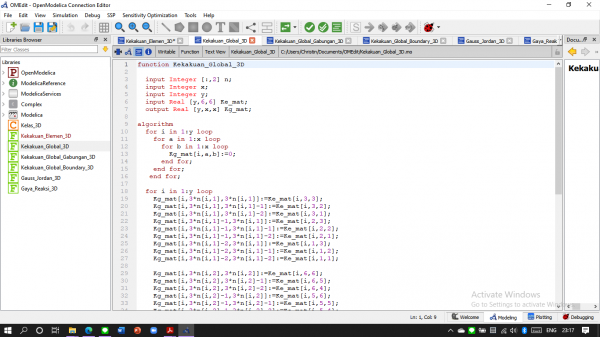
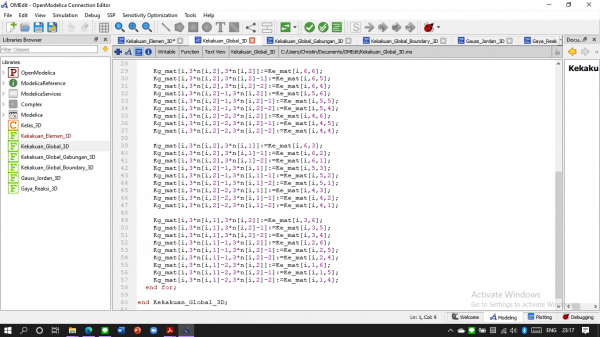
Membuat Kekakuan Global
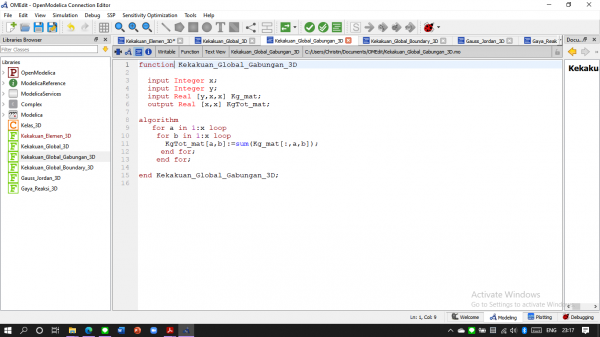
Membuat Kekakuan Global Gabungan (hasil penjumlahan kekakuan global per elemen)
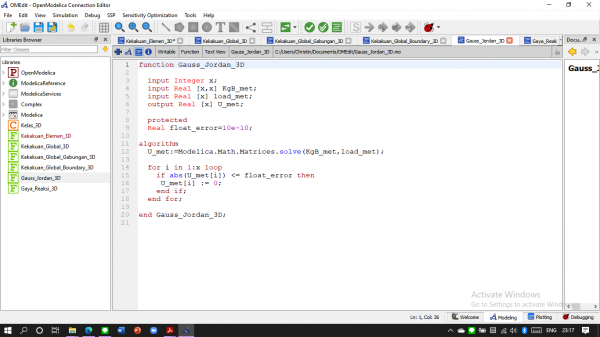
Membuat Gauss Jordan
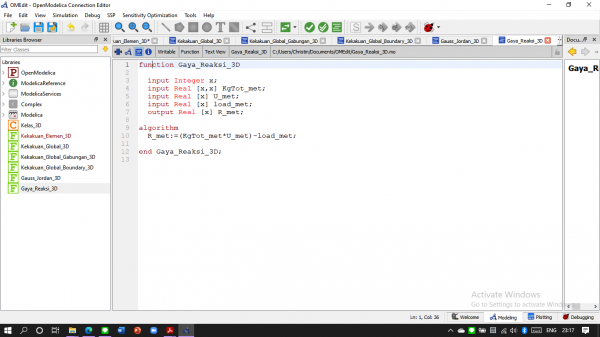
Membuat Gaya Reaksi
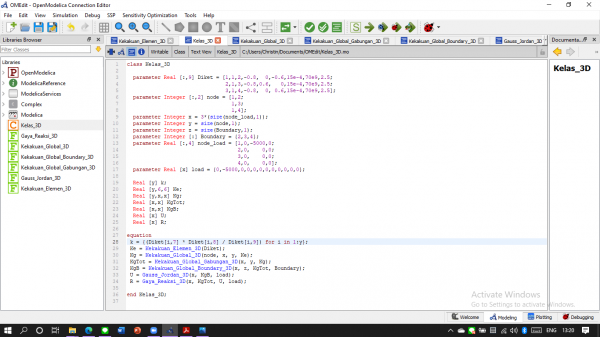
Membuat Kelas Pemanggil
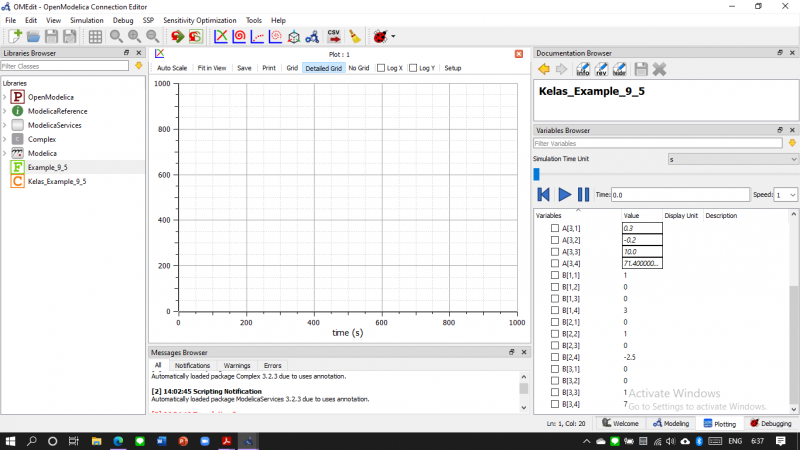
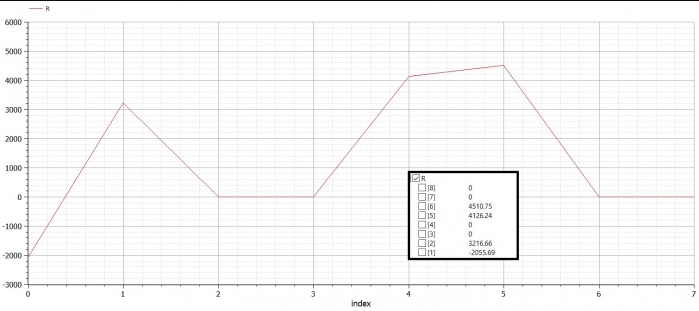
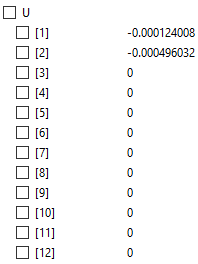
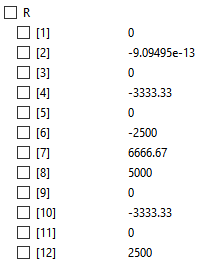
Setelah itu didapatlah hasil untuk U (defleksi) dan R (gaya reaksi)
video penjelasan
12/16/2020
aplikasi metode numerik dalam kasus optimisasi, pada kelas kami diajarkan mengenai optimasi menggunakan modelica yang dijelaskan oleh Bu Chandra dengan menggunakan bracket function. sistem persamaannya sebagai berikut;
FungsiObjek.mo
function FungsiObjek input Real x; output Real y; algorithm y:= 2*Modelica.Math.sin(x)-x^2/10; end FungsiObjek;
Dimana fungsi ini akan menjadi sebuah fungsi yang ada dipanggil dengan file jenis model.
BracketOptimal.mo
model BracketOptimal
parameter Integer n = 8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
Real d;
algorithm
xup := 4;
xlow := 0;
for i in 1:n loop
d:=((5^(1/2)-1)/2) * (xup-xlow);
x1[i] := xlow+d;
x2[i] := xup-d;
f1[i] := FungsiObjek(x1[i]);
f2[i] := FungsiObjek(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow := x2[i];
xopt := xup;
yopt := f1[i];
else
xlow :=xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end BracketOptimal;
Serta File kelas ini akan menjadi fungsi model yang memanggil
Tugas Besar Metnum
"Melakukan Optimasi Rangka Sederhana"
-Tujuan: Mendesain Rangka yang reliable dangan cost yang optimal
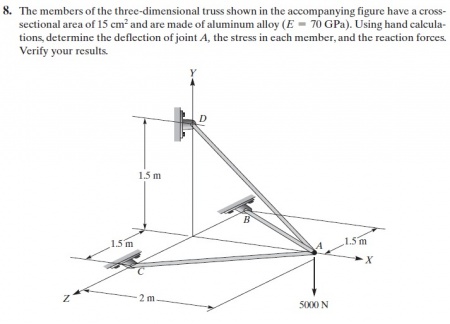
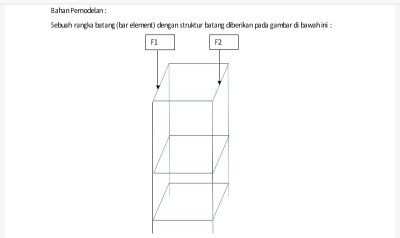
-Geometri dan Load
-Variabel bebas/factor: a. Harga b. Material (Elastisitas properti) c. Area Cross Section Truss (L profile/truss siku)
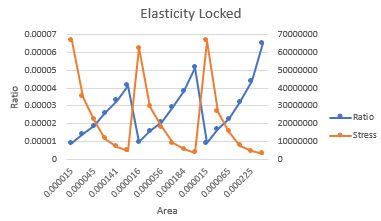
-Membentuk kurva efisiensi harga dengan Curve Fitting
1.Penentuan
- Mengasumsikan bahwa struktur tersebut adalah truses.
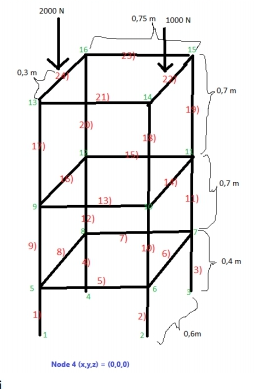
- Beban terdistribusi pada node node yang ada.
- Node 1, 2, 3, dan 4 merupakan fixed
- Beban F1 dan F2 terdistribusi pada node ( node truses yang terkena beban ), node 14 dan 15 sebesar 500N arah y negatif , node 13 dan 16 sebesar 1000N arah y negatif
2.Mencari data dan permodelan
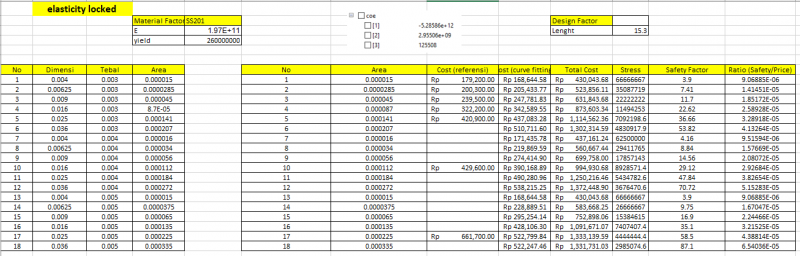
Karena data yang ingin kita cari adalah variasi Elastisitas dan luas profil dari besi siku.untuk mendapatkan variasi yang optimum maka kita mencari referensi tentang variasi material, luas profil dan harga yang ada dipasaran. Setelah didapat seluruh data yang diperlukan disusun dalam bentuk excel untuk proses perhitungan Untuk sistem permodelan 3D-trusses digunakan coding yang sudah dibuat oleh saudara josiah, christopher, dan fahmi. Hasilnya berupa stress pada tiap trusses yang ada distruktur . Untuk memenuhi data yang kurang digunakan permodelan Curve fitting.
3.Perhitungan
Dapat dilihat optimum terjadi pada Material SS304 dengan ukuran 30 x 30 x 3
4. Model Numerik
- 3D-Trusses
model 3D_Trusses_Tubes //define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa) parameter Real Area= (nilai area) ; //Luas Penampang Siku (m2) parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa) //define connection parameter Integer C[:,2]=[ 1,5; // (1)
2,6; // (2)
3,7; // (3)
4,8; // (4)
5,6; // (5)
6,7; // (6)
7,8; // (7)
5,8; // (8)
5,9; // (9)
6,10; // (10)
7,11; // (11)
8,12; // (12)
9,10; // (13)
10,11;// (14)
11,12;// (15)
9,12; // (16)
9,13; // (17)
10,14;// (18)
11,15;// (19)
12,16;// (20)
13,14;// (21)
14,15;// (22)
15,16;// (23)
13,16];//(24)
//define coordinates (please put orderly) parameter Real P[:,6]=[ 0,-0.6,0,1,1,1; //node 1
0.75,-0.6,0,1,1,1; //node 2
0.75,0,0,1,1,1; //node 3
0,0,0,1,1,1; //node 4
0,-0.6,0.4,0,0,0; //node 5
0.75,-0.6,0.4,0,0,0; //node 6
0.75,0,0.4,0,0,0; //node 7
0,0,0.4,0,0,0; //node 8
0,-0.6,1.1,0,0,0; //node 9
0.75,-0.6,1.1,0,0,0; //node 10
0.75,0,1.1,0,0,0; //node 11
0,0,1.1,0,0,0; //node 12
0,-0.6,1.8,0,0,0; //node 13
0.75,-0.6,1.8,0,0,0; //node 14
0.75,0,1.8,0,0,0; //node 15
0,0,1.8,0,0,0]; //node 16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution Real displacement[N], reaction[N]; Real check[3]; Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3]; protected
parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-15, ers=10e-8;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for; //Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for; //Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F); //Solving reaction reaction:=(G_star*displacement)-F; //Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for; //Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for; //Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j]; q2[j]:=P[C[i,2],j]; dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for; //Safety factor for i in 1:Trusses loop
if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if;
end for; end 3D_Trusses_Tubes;
- Function Curve_Fitting
function Curve_Fitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop
for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for;
end for; ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1));
end Curve_Fitting; /* for i in 1:3 loop
for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R);
end for;
- /
- Class Panggil Curve Fitting Elasticity locked (Cost)
class curv_fitting parameter Real X[6]={1.5e-05,2.85e-05,4.5e-05,8.7e-05,14.1e-05,11.2e-05}; parameter Real Y[6]={179200, 200300, 239500, 322200, 420900, 429600};
Real coe[3];
algorithm
coe:=Curve_Fitting(X,Y,2);
end curv_fitting;
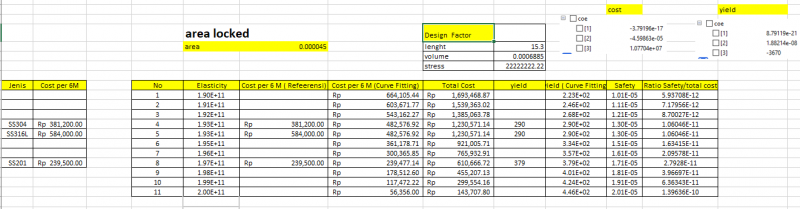
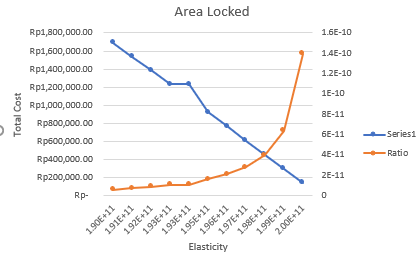
- Class Panggil Curve Fitting Area Locked (Cost)
class class_area1 parameter Real X[3]={1.93E+11,1.93E+11,1.97E+11}; parameter Real Y[3]={381200,584000,239500};
Real coe[3];
algorithm
coe:=Curve_Fitting(X,Y,2); end class_area1;
- Class Panggil Curve Fitting Area Locked ( yield)
class class_area2 parameter Real X[3]={1.93E+11,1.93E+11,1.97E+11}; parameter Real Y[3]={290,290,379};
Real coe[3];
algorithm
coe:=Curve_Fitting(X,Y,2); end class_area2;