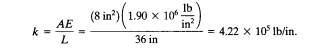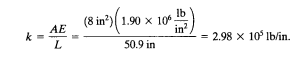Metnum03-Khairul Hasibullah
Assalamualaikum Warahmatullahi Wabarakatuh
Contents
Biodata
Nama: Khairul Hasibullah
NPM : 1806233335
Hobi: Membaca buku
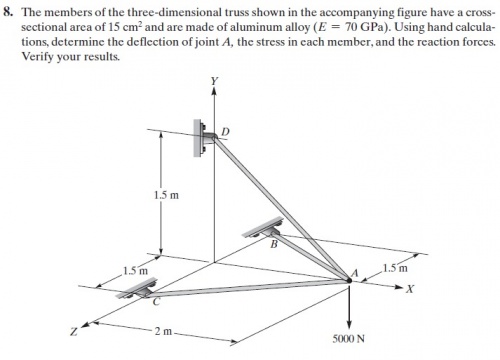
Pertemuan 1
Sebelum UTS Kami mempelajari berbagai hal yaitu:
1. Deret mclaurin Deret mclaurin berkaitan dengan deret taylor dimana deret mclaurin dimana deret mclaurin adalah bentuk khusus dari deret taylor dimana fungsinya diekspansi disekitar c=0
deret mclaurin memiliki bentuk sebagai berikut
Deret mclaurin digunakan untuk membantu kita mencari nilai dari sebuah persamaan dimana akar dari persamaannya yang dicari angka yang tidak bulat, seperti sin 27,5 atau sebagainya
2. Open method and barcekting method Open dan bracketing method merupakan metode yang digunakan untuk mencari nilai akar-akar dari sebuah persamaan, Open method dan bracketing method hanya dibatasi pada kondisi konvergen
open method terdiri simple fixed point, newton raphson, secant , and brents bracketing method terdiri dari graphical method, bisection method, false position method
3. Regresi Linear regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear. Berdasarkan penggunaan variable bebas, maka regresi linear dapat dibagi menjadi dua, yaitu regresi linear univariate dan regresi linear multivariate.
Persamaan umum regresi linear: Y=ax+b
dimana
4. Turunan Numerik
Turunan numerik digunakan dalam menentukan nilai turunan fungsi f berdasarkan pada tabel, dimana ada tiga bentuk turunan yaitu:
a. forward differential
b. backward differential
c. center differential
tutorial open modelica tentang pendulum
https://www.youtube.com/watch?v=CdaQzhmoHDY
Pertemuan 2
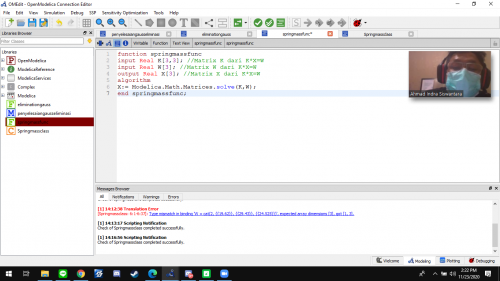
Pada pertemuan 2 kemarin, seperti yang telah dijelaskan sebelumnya, pak Dai memberi kami tugas untuk menyelesaikan salah satu persamaan linear simultan dengan open modelica. saya memilih untuk mengerjakan Metode Gauss Elimination sebagai objek percobaan saya didalam penyelesaian modelica. pertama-tama saya mencari soal tentang 3 persamaan linear 3 variable yang nantinya akan diubah menjadi matriks 3x3 dengan persamaan A*B=C. dimana matriks A[3x3], B[3], dan C[3]. soulusi yang dicari adalah pada nilai B1,B2, dan B3.
berikut contoh soal saya
Setelah itu, persamaan2 tersebut dibuat dalam bentuk matriks sebelum diselesaikan menggunakan gauss, menjadi
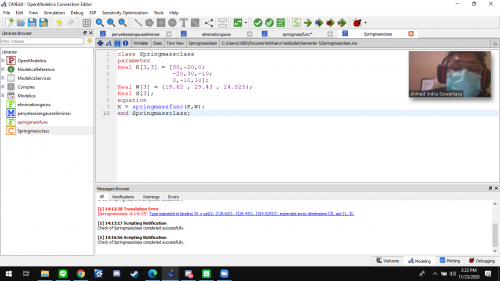
sesuai dengan perintah pak dai, kita dianjurkan membuat 2 kelas dalam modelica. yang pertama adalah kelas function dimana kita memasukan fungsi algoritma nya. dan kelas yang kedua adalah class dimana nanti function tadi di recall dan dimasukan variable nya lalu solve dilakukan..
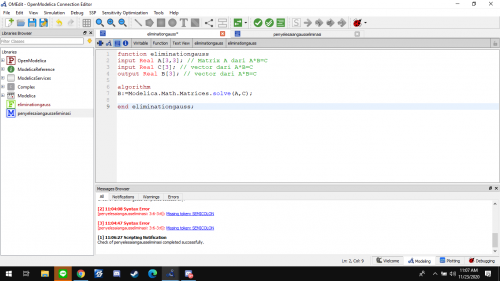
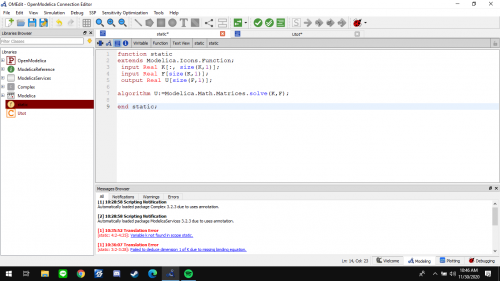
Function Class
function class diisi dengan mendeclare nilai input,outputdan logartima dimana input : A[3,3] dan C[3]
output : B[3]
Logaritma : B:=Modelica.Math.Matrices.solve(A,C)
logaritma menggunakan fungsi yang sudah ada didalam modelica yaitu fungsi matrices untuk gauss elimination.
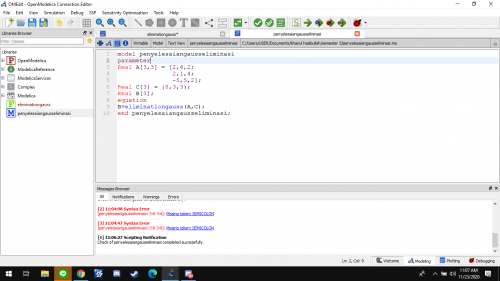
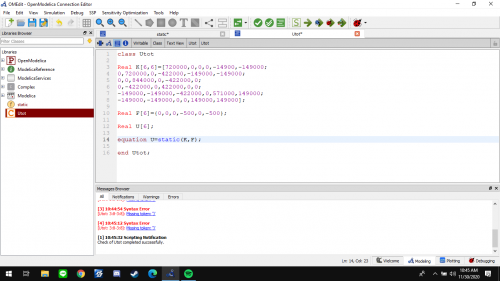
Class gauss elimination
dalam kelas ini, fungsi tadi yang bernama "fungsii" direcall pada kolom equation dengan memasukan A&C sebagai inputnya dan B outputnya. namun sebelum itu terlebih dahulu saya mendeclare nilai2 inputanya tadi seperti digambar atas tersebut.
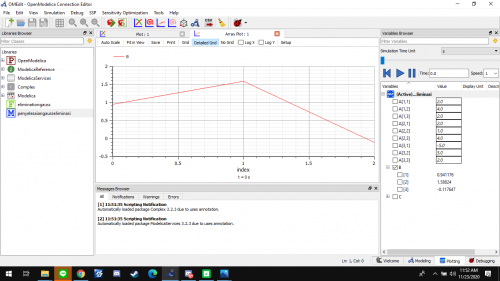
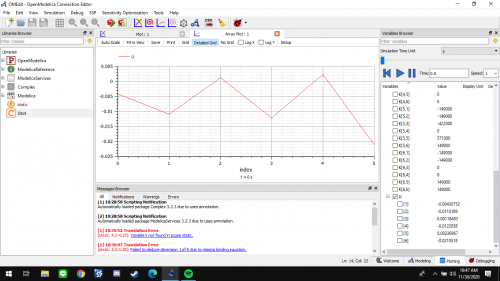
Hasil
setelah itu, kita dapat melakukan plotting dan mendapatkan hasilnya. dari gambar tersebut kita dapat mengetahui nilai dari B adalah = 0.94 , 1.59 , -0.12
PERTEMUAN 3
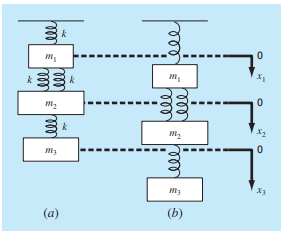
Pada pertemuan ketiga kami mempelajari tentang spring mass system dimana persamaan umum untuk penyelasaian spring mass system menggunakan hukum Hooke
dimana
m: massa benda x: perpindahan Fd dan Fu: merupakan gaya yang bekerja pada benda seperti gaya pegas maupun gaya gravitasi
Ini merupakan contoh yang digunakan pada dibukuu
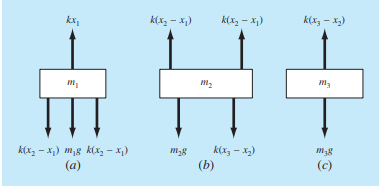
Untuk penjabaran gaya-gaya yang bekerja pada masing-masing massa adalah sebagai berikut:
Selanjutnya untuk massa 1=
1.) Subjek Massa 1
2K(x2-x1)-Kx1+m1g= m d^2 x1/dt^2 dikarenakan tidak adanya percepatan pada sistem maka m d^2 x1/dt^2 =0
3kx1 - 2kx2=m1g ......(1)
2.) Subjek Massa 2
k(x3-x2) - (2k(x2-x1))+m2g=0
-kx3 + 3kx2-2kx1=m2g ......(2)
3.) Subjek Massa 3
-k(x3-x2) +m3g=0
-kx2 + kx3=m3g .......(3)
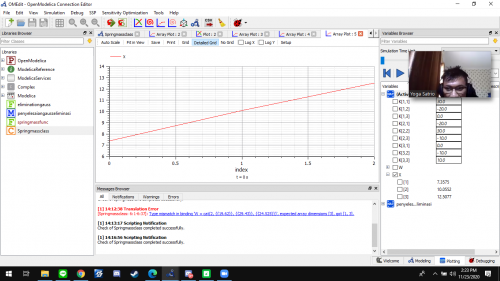
Ini merupakan proses pengerjaan saya pada open modelica
dapat dilihat bahwa nilai x1 = 7.3575; x2 = 10.0552; x3 = 12.5077, sesuai dengan hasil yang ada di buku Metode Numerik.
Setelah pertemuan ini, pak Dai memberikan PR untuk mengerjakan soal berikut:
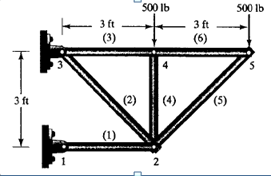
selanjutnya menghitung nilai kekakukan dimana:
-elemen 1,3,4, dan 6 memiliki k yang sama
-elemen 2 dan 5 memiliki k yang berbeda dengan
Ini merupakan penyelesaian menggunakan open modelica
dimana function yang saya buat sebagai berikut:
selanjutnya saya membuat class pada open modelica dengan parameter-parameter dan memanggil function sebagai berikut:
dan yang terakhir ini merupakan nilai U dan plot diagram dari U
Pertemuan 4
QUIZ 01
Berikut penyelesaian flowcart yang saya buat untuk menjawab pertanyaan quiz diatas
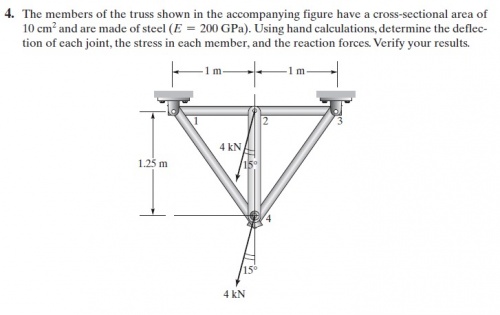
Berikut penyelesaiaan untuk nomor 4
Pertemuan 5
1. Membuat kelas function terlebih dahulu
StiffnessMatrixElement:
function StiffnessMatrixElement
input Real [:,6] inisiasi_mat; output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected Real cos_x; Real cos_y; Real cos_z; Real [6] StiffTrig; Real [6,6] StiffTrans; Real [size(inisiasi_mat,1)] L; Real [size(inisiasi_mat,1)] k_vec;
algorithm
L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)};
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)};
// Finding stiffness matrix of each element member for i in 1:size(inisiasi_mat,1) loop
// Clearing the matrices StiffTrig := zeros(6); StiffTrans := zeros(6,6); // Converting degrees to radians cos_x := inisiasi_mat[i,2]/L[i]; cos_y := inisiasi_mat[i,3]/L[i]; cos_z := inisiasi_mat[i,4]/L[i];
// {cos^2, sin^2, sincos}
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
2. Mengubah ke elemen global
StiffnessMatrixGlobal:
function StiffnessMatrixGlobal
input Integer x; input Integer [:,2] n; input Real [:,6,6] Ke_mat; output Real [size(Ke_mat,1),3*x,3*x] Kg_mat;
algorithm
Kg_mat := zeros(size(Ke_mat,1),3*x,3*x);
for i in 1:size(Ke_mat,1) loop Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; end for;
end StiffnessMatrixGlobal;
3. mennetukan jumlah k global nya
SumStiffnessMatrixGlobal:
function SumStiffnessMatrixGlobal
input Real [:,:,:] Kg_mat; output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat;
algorithm
for a in 1:size(Kg_mat,2) loop
for b in 1:size(Kg_mat,2) loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
4. membuat kelas function check force
untuk memastikan perhitungan yang dilakukan benar atau tidak (force total harus sama dengan 0)
function GaussJordan
input Real [:,:] KgB_met; input Real [size(KgB_met,1)] load_met; output Real [size(KgB_met,1)] U_met; protected Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:size(KgB_met,1) loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
5. Mmembuat kelas fungsi Boundary Stiffness Matrix Global
function BoundaryStiffnessMatrixGlobal
input Real [:,:] KgTot_met; input Integer[:] Boundary_xyz; input Integer[:] Boundary_xy; input Integer[:] Boundary_xz; input Integer[:] Boundary_yz; input Integer[:] Boundary_x; input Integer[:] Boundary_y; input Integer[:] Boundary_z; output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met;
algorithm
for a in 1:size(KgTot_met,1) loop
for b in 1:size(KgTot_met,1) loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
if Boundary_xyz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xyz,1) loop
for b in 0:2 loop
KgB_met[3*(Boundary_xyz[a])-b,i]:=0;
KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xy[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xy,1) loop
for b in 1:2 loop
KgB_met[3*(Boundary_xy[a])-b,i]:=0;
KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xz,1) loop
for b in 0:2:2 loop
KgB_met[3*(Boundary_xz[a])-b,i]:=0;
KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_yz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_yz,1) loop
for b in 0:1 loop
KgB_met[3*(Boundary_yz[a])-b,i]:=0;
KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_x[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_x,1) loop
KgB_met[3*(Boundary_x[a])-2,i]:=0;
KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1;
end for;
end for;
end if;
if Boundary_y[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_y,1) loop
KgB_met[3*(Boundary_y[a])-1,i]:=0;
KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1;
end for;
end for;
end if;
if Boundary_z[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_z,1) loop
KgB_met[3*Boundary_z[a],i]:=0;
KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1;
end for;
end for;
end if;
end BoundaryStiffnessMatrixGlobal;
6. Melakukan Gaus Jordan
atau yang kita sebut matriks U
function GaussJordan
input Real [:,:] KgB_met; input Real [size(KgB_met,1)] load_met; output Real [size(KgB_met,1)] U_met; protected Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:size(KgB_met,1) loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
7. Reaction Force
mencari nilai reksi gaya pada tumpuan
ReactionForce:
function ReactionForce
input Real [:,:] KgTot_met; input Real [size(KgTot_met,1)] U_met; input Real [size(KgTot_met,1)] load_met; output Real [size(KgTot_met,1)] R_met; protected Real float_error = 10e-10;
algorithm
R_met := KgTot_met*U_met-load_met;
for t in 1:size(KgTot_met,1) loop
if abs(R_met[t]) <= float_error then
R_met[t] := 0;
end if;
end for;
end ReactionForce;
Pertemuan 6
Assalamu'alaikum wr.wb. Hari ini Pak Dai menghimbau mahasiswa untuk melakukan muhasabah.Muhasabah yang dilakukan adalah terkait dengan pembelajaran mata kuliah metode numerik ini. Mahasiswa dihimbau untuk menilai diri sendiri sesuai apa yang telah didapat serta konsep yang telah dipahami masing-masing individu.
Selanjutnya, pembelajaran dilanjutkan dengan penjelasan materi oleh Christo terkait dengan alur berfikir mengenai soal-soal yang telah diberikan dan menjelaskannya ke teman-teman yang ada di kelas menggunakan software OpenModelica. Penjelasannya adalah terkait bagaimana mengidentifikasi parameter, membentuk model, serta melakukan perhitungan dari model soal yang digunakan. Selain itu, Ahmad Mohammad dan Josiah Enrigo menjelaskan sebagai perbandingan dari soal-soal yang telah dikerjakan. Terima kasih, Wassalamu'alaikum wr.wb.
Pertemuan 7
Aplikasi Metode Numerik dalam Kasus Optimasi. Optimasi adalah salah satu cara untuk emndapatkan suatu besarna maksimum atau minimum dari suatu masalah. Optimasi yang dijelaskan oleh Bu Chandra adalah mengenai optimasi Bracket Optimization using golden ratio. Penerapan optimasi menggunakan golden ratio ini diharapkan dapat diaplikasikan dalam mengerjakan tugas besar dalam menentukan stress maksimum yang masih saftey pada struktur dan harga yang dikeluarkan untuk digunakan pada struktur secara keseluruhan. Untuk hal tersebut, kekuatan material harus lebih kuat dari stress dari beban yaitu stress dari beban tersebut tidak boleh lebih besar 1/2 kali nya dari kekuatan material.
Optimasi merupakan cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Optimasi yang dilakukan bergantung pada penentuan dua titik(misal xL dan xU) sehingga terdapat satu nilai maksimum atau minimum dari fungsi tersebut pada selang nilai xL dan xU. Berikut adalah langkah-langkah dalam menentukan nilai maksimum dari sebuah fungsi:
1. Menentukan batasan titik awal terendah (xL) dan tertinggi (xH) 2. Mendapatkan nilai x1 dan x2 dari golden ratio (d) 3. Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru 4. Mendapatkan nilai x1 dan x2 baru lanjutkan langkah tersebut hingga mendapatkan nilai maksimum dari fungsi tersebut
selanjutnya untuk dapat menentukan nilai x1 dan x2 membutuhkan persamaan berikut:
d = akar5 - 1/2 x (xu-xl)
x1 = x1 + d
x2 = xu - d
Dalam melakukan optimasi sebuah fungsi dan menentukan nilai xL dan xU baru harus memeperhatikan syarat berikut:
- f(x1) > f(x2), domain sebelah kiri x2 dapat dieliminasi xL = x2 untuk iterasi berikutnya xu = xu lama
- f(x2) > f(x1), domain x sebelah kanan x1 dapat dieliminasi xu = x1 untuk iterasi berikutnya xL = xL lama
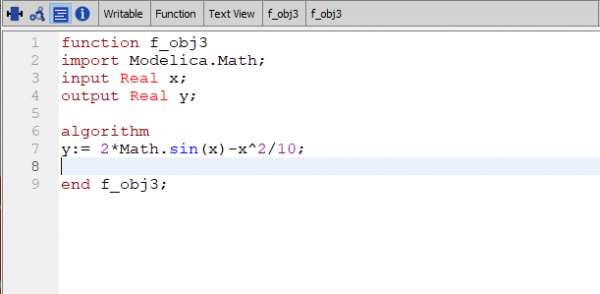
Selanjutnya Bu Chandra memberikan contoh penyelesaian optimasi bracket menggunakan golden ratio yang diaplikasikan pada open modelica
Ini adalah function dari codingnya
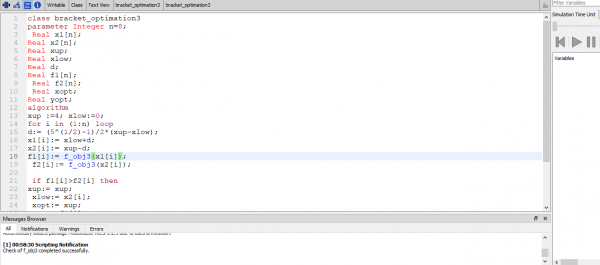
Selanjutnya adalah pembuatan class yang menggunakan metode looping pada pengerjaanya yang dilakukan sebanyak 8 kali
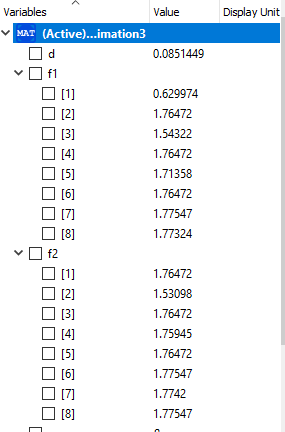
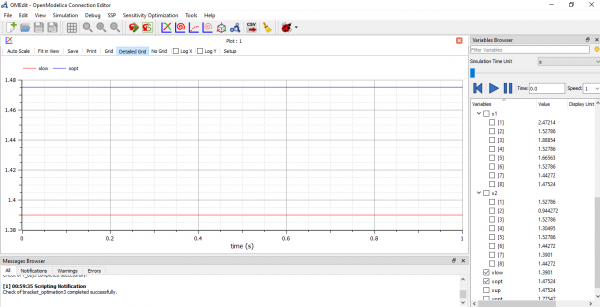
selanjutnya ini adalah hasil dari simulasi open modelica
Kesimpulannya adalah dari penyampaian tugas besar, secara garis besar merupakaan persamaan truss. Fungsi optimasi diharuskan memiliki fungsi objektif seperti mendapatkan stress yang maksimum dan biaya yang minimum. Lalu, variabel yang dapat diubah merupakan dimensi dari truss siku dan juga raw materialnya.
TUGAS BESAR METODE NUMERIK
Soal dan asumsi
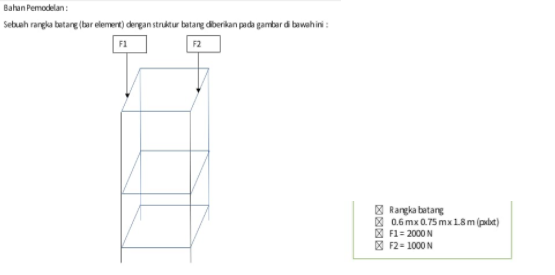
Pada tugas besar ini, kami diberikan sebuah tugas untuk melakukan optimisasi pemilihan material dan luas penampang trusses yang akan digunakan untuk membuat konstruksi sebagai berikut:
Diketahui:
F1=2000 N F2=1000 N spesifikasi truss geometri truss(berbentuk siku)
Asumsi yang diberikan:
-variasi stiffness terkait dengan material yang digunakan -beban terdistribusi pada node (karena trusses) -safety factor bernilai 2 -batas displacement 0,001 m sebelum buckling
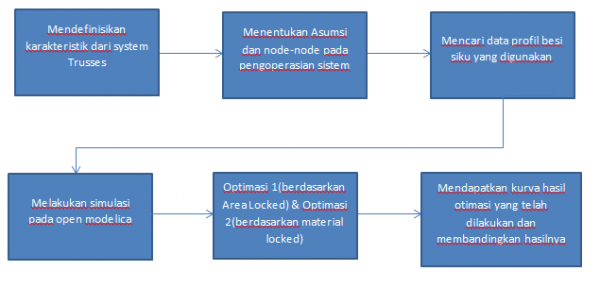
Tahapan pengerjaaan
Berikut adalah tahapan-tahapan dalam penyelesaian soal tugas besar yang telah diberikan yang telah dirangkum pada flowcart dibawah
Coding
Pertama-tama tentukan dahulu parameter variabel yang diketahui dan yang telah ditentukan, dimana terdapat 16 node dan juga 24 batang trusses dimana pada pembahasan coding ini telah ditentukan material yang digunakan adalah SS 304 dengan nilai elastisitas 193 x 10^9 N/m^2
//define initial variable
parameter Integer Points=16; //Number of Points
parameter Integer Trusses=24; //Number of Trusses
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004)
parameter Real Elas=193e9; //Elasticity SS 304
//define connection
parameter Integer C[:,2]=[ 1,5; // (1)
2,6; // (2)
3,7; // (3)
4,8; // (4)
5,6; // (5)
6,7; // (6)
7,8; // (7)
5,8; // (8)
5,9; // (9)
6,10; // (10)
7,11; // (11)
8,12; // (12)
9,10; // (13)
10,11;// (14)
11,12;// (15)
9,12; // (16)
9,13; // (17)
10,14;// (18)
11,15;// (19)
12,16;// (20)
13,14;// (21)
14,15;// (22)
15,16;// (23)
13,16];//(24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;