Irfan Setio Leksono

Pertemuan Pertama

Irfan Setio Leksono

1606883644

Teknik Perkapalan

Pada hari Rabu tanggal 6 Februari 2019, saya dan teman teman mahasiswa teknik perkapalan yang lain mengikuti kelas mata kuliah Metode Numerik di LabPuskom FTUI. Dr. Ahmad Indra adalah fasilitator kami pada hari itu, beliau kerap disapa dengan panggilan Pak DAI, yaitu singkatan dari nama beliau, beliau adalah salah satu dosen dari Departemen Teknik Mesin Fakultas Teknik Universitas Indonesia.

Jadi menurut penjabaran dari pak DAI, Tujuan dari mempelajari metode numerik ini antara lain : - untuk memahami konsep/prinsip dan mampu menerapkannya - menjadi orang yang lebih mengenal siapa dirinya

Pada hari itu pak DAI juga mengatakan bahwa "matematika itu bisa membantu dan bisa juga menyesatkan, jadi harus mengerti bahasa matematika yang anda tulis". Menurut saya pernyataan itu sangat tepat karena kita sebagai mahasiswa Fakultas Teknik wajib memahami mataematika itu secara mendalam, agar kita tidak tersesat oleh bahasa matematika tersebut.

Sebagai mahasiswa kitapun tidak boleh mengikuti dosen secara "blind follower", taklit, atau fanatik. Sebaiknya kita mahasiswa dapat mengargumentasikan apa yang diberikan oleh dosen agar mahasiswa dapat berpikir rasional dan kreatif.

Saat itu pak DAI juga memberikan salah satu contoh soal matematika yaitu A=x^-1/x-1, jika x=1, maka berapa nilai A? Dari salah satu sudut pandang mahasiswa yang ada di kelas ini, soal ini dapat diselesaikan dengan pendekatan limit, jika dengan pendekatan limit maka persamaan A tersebut didifferensialkan terlebih dahulu, lalu nilai x tersebut digantikan oleh nilai 1, sehingga didapatkan hasil A=2.

Outline Metode Numerik :

1. Algoritma, Flowchart, pemrograman, metode literative

2. Penyelesaian persamaan aljabar simultan

3. Differensial dan Integral

4. Optimasi

5. Studi Kasus

Pertemuan ke-2

Penyelesaian Masalah dengan Metode Numerik

Pada pertemuan kedua ini kami diajarkan oleh pak DAI bagaimana sebuah masalah teknik dibuat menjadi model matematis sehingga dapat dipecahkan dan ditemukan solusinya.

Langkahnya yaitu melalui teoritis lalu dilakukan percobaan. Metode numerik adalah salah satu model matematis yang memiliki peritungan untuk menyelesaikannya.

Skemanya adalah seperti :

Masalah Teknik ---> Model Matematis ---> Algoritma ---> Program Komputer ---> Hasil Numerik ---> Visual ---> Interpretasi ---> Solusi

Salah satu contohnya dalam dunia perkapalan adalah kita dapat menghtung efisiensi dari penggunaan bahan bakar kapal dalam satu kali perjalanan antara Jakarta ke Surabaya, selain itu kita juga dapat menghitung jarak susunan pipa paling efektif di dalam kamar mesin. Kita dapat memecahkan masalah ini tanpa harus melakukan percobaan secara langsung, namun dengan menggunakan sistem ini kita dapat mengetahui hasilnya dengan lebih baik.

Tugas Metode Numerik dengan Python

Tugas ini mencoba menyelesaikan pertidaksamaan linear dengan menggunakan bahasa Python. Pertidaksamaannya adalah :

ax + by = c px + qy = r

Nilai a, b, p, q adalah konstanta dengan nilai tertentu. x dan y adalah variabel yang merupakan solusi dari pertidaksamaan tersebut. Dengan menggunakan python kita harus bisa menyelesaikan masalah itu. Berikut adalah program untuk menyelesaikan pertidaksamaan linear dengan menggunakan python:

import numpy as np

print("Please input the value")

a = int(input("input value of a :"))

b = int(input("input value of b :"))

c = int(input("input value of c :"))

p = int(input("input value of p :"))

q = int(input("input value of q :"))

r = int(input("input value of r :"))

x = np.array([[a,b],[p,q]])

y = np.array([c,r])

z = np.linalg.solve(x,y)

xval = int(z[0])

yval = int(z[1])

print("x = ",xval)

print("y = ",yval)

semoga dengan ilmu yang diberikan oleh pak DAI dan kolega ini, kami dapat mengaplikasikannya dengan baik ke depannya

Pertemuan ke-3 20 Februari 2019

Pada pertemuan kali ini, kami mendapatkan materi tentang Aljabar Linear yang berguna untuk menggunakan Aplikasi Python oleh bang Edo Hilman M'14.

Kerja dari python hanya bisa jumlah, kali, bagi, caranya bagaimana? kita harus menggunakan deret. Dan kuncinya adalah pola.

Materi Aljabar Linear yang diajarkan pada hari ini adalah eliminasi matrix menggunakan metode Gauss.

Numerik itu identik dengan iterasi, iterasi itu identik dengan pola.

Untuk mendalami aplikasi python, kami dapat membaca dan memahaminya lebih jauh pada buku python di Bab 1.

Tugas : buka file dari IDLE, file --> open. Menggunakan matrix di buku halaman 20.

Cari matrix lain 3x3. Berikan penjelasan + alurnya dari code yang telah diberikan.

Dalami dan pahami tugas yang diberikan, karena materi ini sangat bermanfaat.

Harapannya adalah dengan belajar ini kalian punya mainset, apa itu mainset, kita dapat berkomunikasi dengan orang orang yang berkecimpung dengan code code.

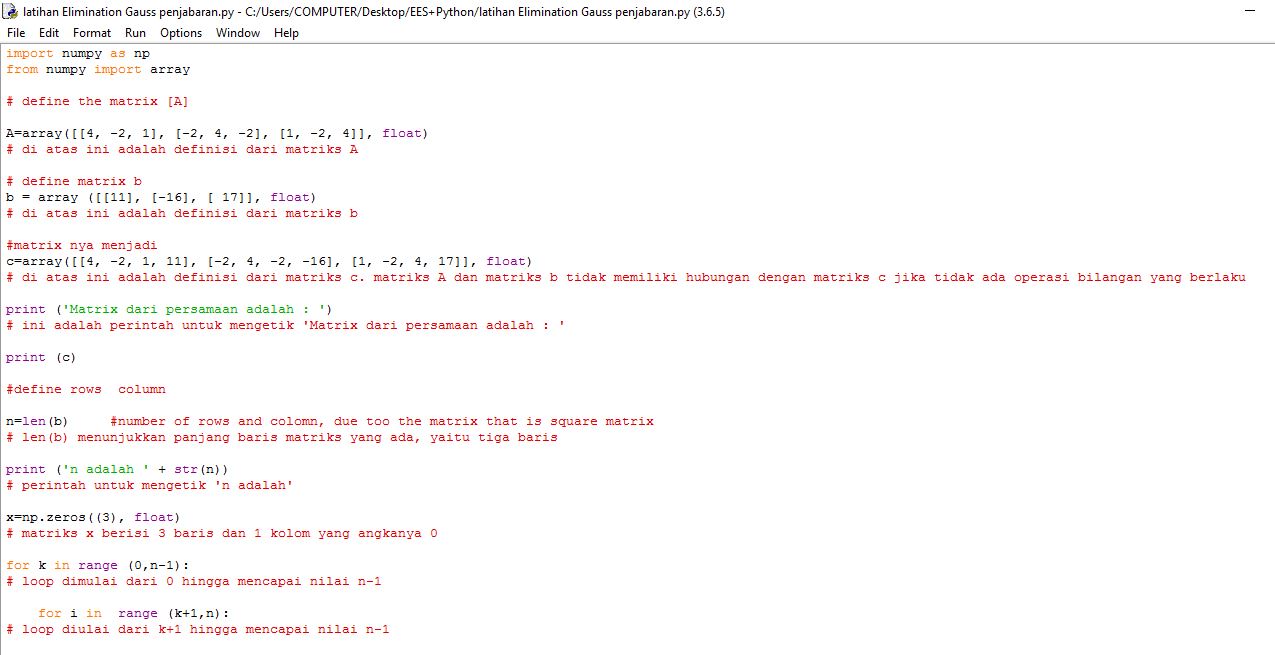
PR Eliminasi Gauss

28 Februari 2019

Pada pertemuan kali ini Bang Edo M'14 mengajarkan kita tentang penggunaan numpy untuk menyelesaikan aljabar linear. Kita mengimport numpy pada python dengan tujuan agar module numerical python yang akan dipergunakan untuk menyelesaikan masalah numerik sudah terpasang pada aplikasi yang kita buat. Karena jika ini belum dilakukan maka kita tidak bisa menjalankan aplikasi python yang akan kita operasikan. Mengakses numpy dengan syntax "np." seperti np.array atau np.linalg bergantung pada kebutuhan. np.array dipergunakan untuk mengakses sub bab array dari modul numerical python untuk membuat matriks. Syntax print sebuah text harus diberi tanda kutip seperti print("Hello World"). Untuk print sebuah text dan variable a dapat ditulis print("Variabel A adalah" , a). Len() digunakan untuk mengukur panjang baris dari matriks yang ada. Looping pada python bisa dipergunakan syntax for atau if dengan kondisi tertentu sesuai kasus yang ada seperti for k in range(0,n-1). Jarak menjorok ke dalam mengartikan bahwa syntax yang ada adalah bagian dari syntax sebelumnya sehingga saling berkaitan. Kita diajarkan mengenai bagaimana syntax eliminasi gauss jordan pada python. Di akhir pertemuan ini kami ditugaskan untuk mencoba menyelesaikan permasalahan aljabar linear yaitu menghitung break even point dalam membangun usaha kos kosan.

Pertemuan 6 Maret 2019

Pada hari ini kami diajarkan dan diperintahkan untuk menghitung persamaan pada perhitungan struktural sederhana (pada pegas) --> buat persamaan --> pecahkan

Contoh kasus 1 :

Ada bangunan dan memiliki 4 titik secara berurutan, titik 1 diatas dan titik 4 paling bawah, maka tentukan tegangan dan regangan paling tinggi.

hasil : tegangan terjadi pada titik 1, regangan terjadi pada titik 4

Contoh kasus 2 :

Kerjakan menggunakan python persamaan berikut.

2x-2y=1 4x-6y=1

hasilnya tidak dapat diselesaikan karena tidak menemukan titik temu, maka hal yang dapat diambil dari sini adalah sebelum mengoperasikan dengan Pyhton, kita harus menelaah terlebih dahulu apakah persamaan ini dapat diselesaikan atau hanya sebagai pengecoh yang tidak dapat diselesaikan.

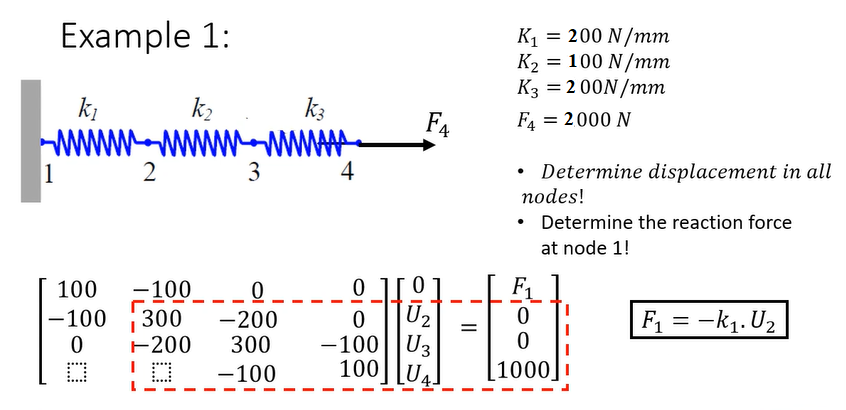
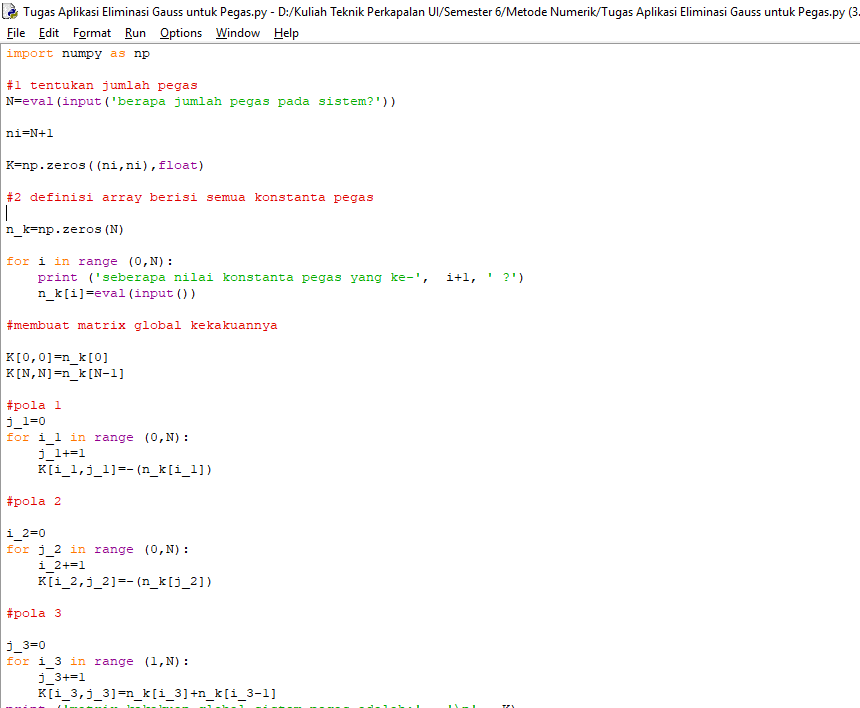
Tugas 5 Metode Numerik

Aplikasi Eliminasi Gauss pada sistem pegas yang disusun seri

Jika pada soal diketahui konstanta pegas 1, 2, dan 3 serta gaya yang bekerja pada pegas.

Pengaplikasian gaya pegas yang disusun seri pada Python :

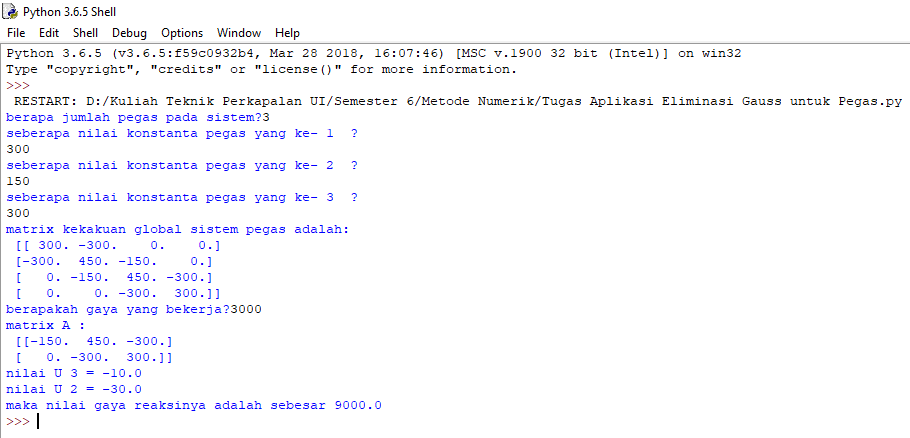
Pertemuan 13 Maret 2019

Pada pertemuan kali ini kami mempelajari lebih dalam mengenai command command yang kita masukkan ke aplikasi python untuk menyelesaikan permasalahan gaya aaksi reaksi pada pegas.

import numpy as np

print('Aplikasi Sistem Pegas Menggunakan Metode Numerik') print('Pegas Dengan Susunan Seri')

N=eval(input('berapa jumlah pegas pada sistem ?'))

1. jumlah pegasnya

ni=N+1 #ni adalah jumlah nodenya K=np.zeros((ni,ni),float)

1. 2. definite array yang berisi semua konstanta pegas

n_k=np.zeros(N)

for i in range (0,N) :

   print('berapakah nilai konstanta pegas yang ke ',i+1, ' ?')
   n_k[i]=eval(input())

print (n_k) K[0,0]=n_k[0] K[N,N]=n_k[N-1]

1. pola 1

K[0,0]=n_k[0] K[N,N]=n_k[N-1]

1. pola 2

j_2 = 0 for (i_2) in range (0,ni-1) :

   j_2+=1
   K[i_2,j_2] =-(n_k[i_2])

1. pola 3

i_3 = 0 for (j_3) in range (0,ni-1) :

   i_3+=1
   K[i_3,j_3]=-(n_k[j_3])

1. pola 4

j_4 = 0 for (i_4) in range (1, ni-1) :

   j_4+=1
   K[i_4,j_4] = n_k[i_4]+n_k[i_4-1]

print (K) print ('matrix konstanta kekakuan global sistem pegasnya adalah','\n',K)

Aplikasi FEM pada 2 material

import numpy as np

1. menentukan jumlah pegas

N = 2

ni = N+1

K = np.zeros((ni,ni),float)

1. mendefinisikan array berisi konstanta pegas

n_k = np.zeros(N) D=np.zeros(N) E=np.zeros(N) L=np.zeros(N) A_i=np.zeros(N) A = np.zeros(N) E_L=np.zeros(N) for i in range (0,N) :

   print ('Berapa diameter material', i+1,'?')
   D[i]=eval(input())
   print ('Berapa nilai modulus young material', i+1,'?')
   E[i]=eval(input())
   print ('Berapa panjang material', i+1,'?')
   L[i]=eval(input())
   A_i[i]=float(D[i]*D[i])
   A[i]=float(A_i[i] * 0.765)
   E_L[i]=float(E[i]/L[i])
   n_k[i]=float(A[i]*E_L[i])
   print('Nilai konstanta pegas ke-', i+1, 'adalah', n_k[i])

print('Berapakah jarak antara titik B dengan material?') h = eval(input())

1. membuat matriks global kekuatan

K[0,0]=n_k[0]

K[N,N]=n_k[N-1]

1. pola1

j_1=0 for i_1 in range (0,N) :

   j_1+=1
   K[i_1,j_1]=-(n_k[i_1])

1. pola2

i_2=0 for j_2 in range (0,N) :

   i_2+=1
   K[i_2,j_2]=-(n_k[j_2])

1. pola3

j_3=0 for i_3 in range (1,N) :

   j_3+=1
   K[i_3,j_3]= n_k[i_3]+n_k[i_3-1]

print ('matrix kekakuan global sistem pegas adalah:', '\n', K)

Fn= eval(input('berapakah gaya yang bekerja?'))

A=K[i:ni, 1:ni]

n=len (A)

B=np.zeros(n, float) B[n-1]=Fn

1. eliminasi gauss

for k in range (0,n-1):

   for i in  range (k+1,n):
       if A[i,k] != 0.0 :
           lam = A[i,k]/A[k,k]
           A[i, k:n] = A[i, k:n] - lam*A[k, k:n]
           B[i]=B[i]-(B[k]*lam)

print ('matrix A :', '\n', A)

1. substitusi kembali

U=np.zeros(n,float) for m in range (n-1,-1,-1) :

   U[m]=(B[m]-np.dot(A[m,m+1:n], U[m+1:n]))/A[m,m]
   print('nilai U', m+2, '=', U[m])

if(U[n-1]>h):

   print('Defleksi melebihi batas maksimum!')

else:

   print('Defleksi senilai:', U[n-1])