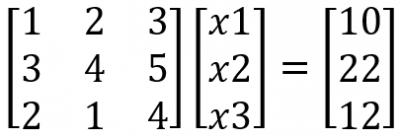Richardo Ariyanto

Biodata
Nama	Richardo Ariyanto
Tempat Tanggal Lahir	Bogor, 5 Januari 2001
NPM	1906301280
Email	richardo.ariyanto@ui.ac.id
Youtube	https://www.youtube.com/c/RichardoAriyanto/
Hobi	Fotografi

Halo! Perkenalkan, nama saya adalah Richardo Ariyanto (1906301280), mahasiswa Teknik Mesin angkatan 2019, Fakultas Teknik, Universitas Indonesia. Saya bercita-cita untuk masuk ke program studi Teknik Mesin sejak dari masuk SMA.

Catatan Minggu Pertama (11 November 2020)

Tujuan Pembelajaran

• Memahami konsep dan prinsip dasar metode numerik
• Dapat menerapkan pemahaman yang didapatkan dalam mata kuliah Metode Numerik
• Mampu menerapkan pemahaman metode numerik dalam bidang keteknikan
• Membentuk kita menjadi orang yang lebih beradab

Manfaat Belajar bagi Diri Saya Sendiri

Menurut saya, pembelajaran adalah suatu proses untuk memahami peristiwa-peristiwa yang terjadi di sekitar kita. Saya merasakan bahwa dengan belajar, saya dapat lebih memahami tentang peristiwa-peristiwa yang terjadi di lingkungan saya, dan membantu saya untuk memecahkan permasalahan baru yang sebelumnya belum pernah saya temukan. Belajar juga dapat meningkatkan kepekaan sosial, kepedulian dan empati dalam diri saya.

Komputer dalam Metode Numerik

Komputer merupakan alat hitung yang sangat cepat, namun pada hakikatnya, komputer bersifat "dummy" dan mempunyai batasan-batasan hitungan yang tidak dapat dilewati. Apa artinya bagi diri saya adalah saya menyadari bahwa komputer merupakan alat hitung yang cepat, namun pada akhirnya semuanya bergantung kepada sang pengguna itu sendiri, sehingga kita harus bisa lebih percaya diri dan menyadari bahwa kemampuan kita bahkan lebih diatas komputer manapun.

Sebelum UTS

Sebelum UTS saya telah mempelajari

• Deret Mclaurin & Deret Taylor, dengan metode forward, center, dan backward
• Bracketing Methods dan Open Methods, dimana bracketing methods meliputi graphical methods, bisection methods, dan false-position methods sedangkan open methods meliputi simple fixed-point iteration, newton-raphson methods, secant methods, dan brents methods
• Mencari nilai interpolasi dan regresi linier menggunakan matriks

Tugas Minggu Pertama

Dalam kesempatan kali ini saya membuat suatu video pembelajaran mengenai penggunaan aplikasi OpenModelica pada perhitungan interpolasi tabel Saturated Liquid-Vapor dalam Termodinamika :

Berikut adalah bahasa Modelica yang saya gunakan untuk membuat interpolasi

model SaturatedWater

parameter Real T1=50;//(C)

parameter Real T2=55;//(C)

parameter Real T=52;//(C)

parameter Real P1=0.1235;//(bar)

parameter Real P2=0.1576;//(bar)

parameter Real SVL1=1.0121*10^(-3);//(m^3/kg)

parameter Real SVL2=1.0146*10^(-3);//(m^3/kg)

parameter Real SVV1=12.032;//(m^3/kg)

parameter Real SVV2=9.568;//(m^3/kg)

parameter Real IEL1=209.32;//(kJ/kg)

parameter Real IEL2=230.21;//(kJ/kg)

parameter Real IEV1=2443.5;//(kJ/kg)

parameter Real IEV2= 2450.1;//(kJ/kg)

parameter Real ESL1=209.33;//(kJ/kg)

parameter Real ESL2=230.23;//(kJ/kg)

parameter Real EEVAP1=2382.7;//(kJ/kg)

parameter Real EEVAP2=2370.7;//(kJ/kg)

parameter Real ESV1=2592.1;//(kJ/kg)

parameter Real ESV2=2600.9;//(kJ/kg)

parameter Real ENSL1=0.7038;//(kJ/kg*K)

parameter Real ENSL2=0.7679;//(kJ/kg*K)

parameter Real ENSV1=8.0763;//(kJ/kg*K)

parameter Real ENSV2=7.9913;//(kJ/kg*K)

Real P;

Real SVL;

Real SVV;

Real IEL;

Real IEV;

Real ESL;

Real EEVAP;

Real ESV;

Real ENSL;

Real ENSV;

equation

P=P1+((T-T1)/(T2-T1))*(P2-P1);

SVL=SVL1+((T-T1/T2-T1))*(P2-P1);

SVV=SVV1+((T-T1/T2-T1))*(SVV2-SVV1);

IEL=IEL1+((T-T1/T2-T1))*(IEL2-IEL1);

IEV=IEV1+((T-T1/T2-T1))*(IEV2-IEV1);

ESL=ESL1+((T-T1/T2-T1))*(ESL2-ESL1);

EEVAP=EEVAP1+((T-T1/T2-T1))*(EEVAP2-EEVAP1);

ESV=ESV1+((T-T1/T2-T1))*(ESV2-ESV1);

ENSL=ENSL1+((T-T1/T2-T1))*(ENSL2-ENSL1);

ENSV=ENSV1+((T-T1/T2-T1))*(ENSV2-ENSV1);

end SaturatedWater;

Catatan Minggu Kedua (18 November 2020)

Dalam perkuliahan minggu ini, terdapat beberapa catatan penting :

• Dalam menjalani proses pembelajaran, orang yang merugi adalah orang yang sama dengan hari kemarin. Hal ini menurut saya adalah fakta, lantas mengapa demikian? Karena ketika sama dengan hari kemarin, orang lain pasti akan senantiasa untuk menjadi "lebih" dalam bidangnya masing-masing, sehingga ketika kita sama dengan hari kemarin maka bukan berarti kita diam, melainkan kita mengalami kemunduran karena orang lain sudah bergerak lebih maju dari kita.
• Dalam metode numerik, segalanya berpusat dalam perhitungan. Dalam proses perhitungan sendiri merupakan suatu seni untuk menyusun algoritma yang cepat, efisien, dan menghasilkan output yang akurat.
  • Dalam dunia Engineering, faktor cepat dan akurat memegang peranan yang penting dalam penggunaan di lapangan. Sebagai seorang calon Engineer, kita memerlukan suatu sistem yang dapat memenuhi dua aspek penting sebelumnya untuk menyelesaikan permasalahan secara efisien baik di lapangan maupun dalam proses perancangan.
  • Pak Dai berkata bahwa saat ini, bahasa mesin yang cepat untuk mengeluarkan nilai outputnya adalah bahasa Fortran dan C. Namun beliau lebih memilih untuk menggunakan bahasa Modelica dalam mata kuliah Metode Numerik karena beberapa alasan:
    • Modelica adalah bahasa pemodelan, yang artinya dapat dimengerti dengan lebih mudah oleh individu yang bukan berlatar belakang dari bidang Ilmu Komputer, sehingga bisa diterapkan di bidang Teknik.
    • Modelica dapat mengeluarkan hasil hitungan yang cepat karena menggunakan bahasa pemrograman C
    • Modelica merupakan suatu bahasa yang open source, sehingga gratis dan mudah diakses oleh semua orang, serta memiliki komunitas pengguna yang cukup banyak.
• Dalam menggunakan OpenModelica, untuk melakukan suatu perhitungan, maka variabel haruslah didefinisikan.
  • Apabila variabel tersebut memiliki nilai; maka nilai tersebut haruslah ditulis dengan menggunakan parameter Real variabel=nilai
  • Apabila variabel tersebut merupakan persamaan atau sesuatu yang ingin kita cari, maka variabel tersebut harus dituliskan dalam equation.

Tugas Minggu Kedua

Di tugas kedua ini, Pak Dai meminta saya dan rekan-rekan mahasiswa Metode Numerik 02 untuk membuat sebuah class dan fungsi panggil. Disini saya akan melakukan sebuah contoh soal mencari penyelesaian dari suatu grafik menggunakan perintah Modelica.Math.Matrices.solve

Pada contoh soal kali ini saya akan mencoba untuk menyelesaikan bentuk matriks Ax=B sebagai berikut:

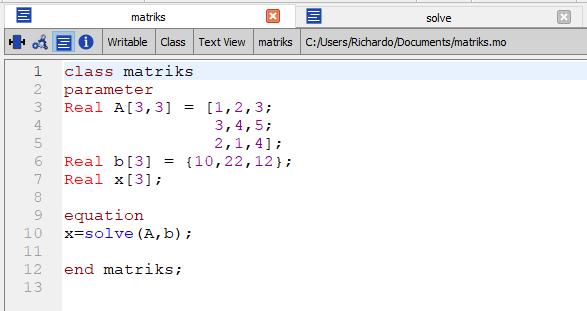
Kemudian saya akan membuat sebuah class yang berisi matriks yang akan saya operasikan.

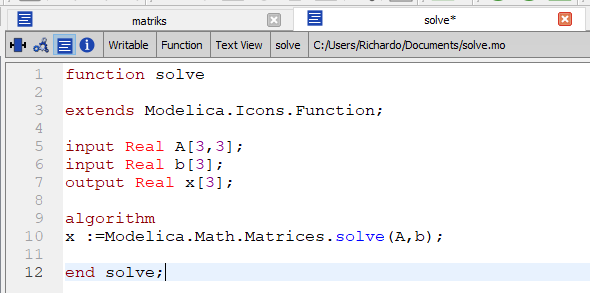
Lalu saya akan membuat sebuah fungsi baru yang berfungsi untuk "memanggil" matriks yang ada di dalam class untuk dioperasikan.

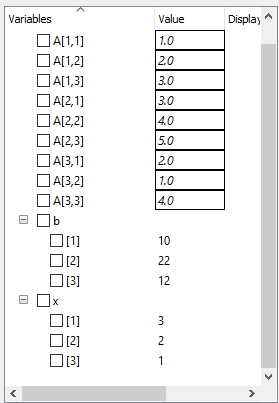
Langkah selanjutnya adalah saya akan mengklik perintah simulate untuk mendapatkan hasil perhitungannya, dan berikut adalah hasil dari x1, x2 dan x3.

Berikut adalah video penjelasan singkat saya untuk tugas minggu kedua.

Catatan Minggu ke-3 (Rabu, 25 November 2020)

Pengenalan secara Mandiri

Di minggu ke-3 ini, Pak Dai meminta mahasiswa untuk mempelajari mengenai aplikasi Metode Numerik pada bidang Engineering, salah satunya adalah Truss. Namun sebelum melangkah lebih jauh, saya terlebih dahulu menonton video dari Youtube untuk membantu saya memahami mengenai metode penghitungan yang digunakan pada Truss, yaitu Finite Element Analysis (FEA). Berikut adalah video yang saya tonton untuk membantu saya memahami mengenai Finite Element Analysis.

Dalam video pengenalan ini, terdapat beberapa hal yang cukup penting dan fundamental untuk memahami perhitungan FEA, yaitu:

• Pada prinsipnya, FEA merupakan suatu metode untuk memecahkan masalah yang kompleks dengan cara memecahnya menjadi masalah yang lebih kecil yang dapat dimodelkan secara matematis, lalu menggabungkan hasil pemodelannya kembali untuk memodelkan solusi dari permasalahan kompleks.
• Kunci dari Finite Element Analysis adalah geometri (bentuk dari model yang akan kita analisis) dan material (bahan penyusun model yang akan kita analisis). Hal ini penting untuk menyelesaikan pemodelan FEA.
• Adapun material yang kita gunakan dalam FEA selanjutnya kita sebut dengan "Mesh". Mesh sendiri menurut apa yang saya pahami merupakan bagian pengisi dari model geometri yang akan kita analisis, dan merupakan bentuk penyusun masalah kecil dari masalah keseluruhan. Contoh dari Mesh adalah:
  • Kita menggunakan garis sebagai mesh untuk memodelkan suatu beam
  • Kita menggunakan silinder sebagai mesh untuk memodelkan batang pohon, dsb.
• Contoh pengaplikasian nyata yang dibahas pada video ini adalah Crash Test dari suatu kendaraan.
  • Sebelum mengenal metode FEA, para insinyur harus mengetes keamanan mobil dengan cara melakukan tes kecelakaan pada produknya. Hasilnya memang akurat dan merupakan "real world test", namun cara seperti ini memakan banyak waktu, biaya dan tenaga yang tidak sedikit.
  • Setelah adanya metode FEA, insinyur dapat memodelkan objek (dalam hal ini kendaraan) kedalam suatu model FEA, dan melakukan simulasinya dengan komputer, sehingga menghemat waktu dan biaya serta mendapatkan hasil dengan cepat.

Setelah saya memahami dasar dari apa itu metode FEA, saya kemudian mempelajari video yang dibuat oleh Mahesh Gadwantikar yang membahas tentang problem dasar pada elemen Truss menggunakan Finite Element Analysis. Berikut adalah tautan videonya

Catatan Kelas

Dalam perkuliahan, Pak Dai berkata bahwa untuk menyelesaikan permasalahan keteknikan, dibutuhkan suatu urutan kerangka berpikir, yaitu

• Menganalisis permasalahan yang dihadapi.
• Melakukan pemodelan secara matematis.
• Menerjemahkan model matematis menjadi bahasa pemodelan yang dapat diolah oleh komputer.
• Melakukan perhitungan model matematis di komputer dan mendapatkan hasilnya.

Tugas 3

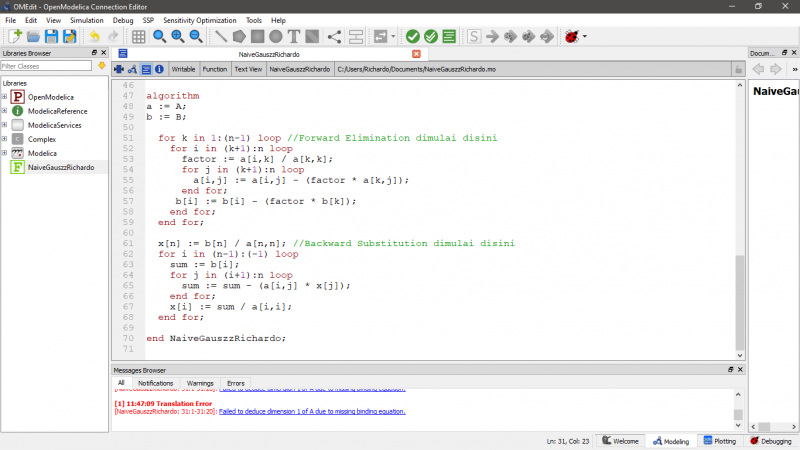
Dalam tugas ke 3 ini saya mencoba untuk menerjemahkan pseudocode yang ada pada Figure 9.4 di Buku Chapra menjadi bahasa Modelica. Berikut adalah bahasa Modelica yang telah saya buat.

function NaiveGauszzRichardo

//Pseudocode dari Figure 9.4 buku Chapra

//Forward Elimination

//DOFOR k = 1, n - 1

// DOFOR i = k + 1, n

// factor = a[i,k] / a[k,k]

// DOFOR j = k + 1 to n

// a[i,j] = a[i,j] - factor * a[k,j]

// END DO

// b[i] = b[i] - factor * b[k]

// END DO

//END DO

//Backward Elimination

//x[n] = b[n] / a[n,n]

//DOFOR i = n - 1, 1, -1

// sum = b[i]

// DOFOR j = i + 1, n

// sum = sum = a[i,j] * x[j]

// END DO

// x[i] = sum / a[i,i]

//END DO

//Naive-Gauss Algorithm

//Richardo Ariyanto

//Metode Numerik 02

//Desember 2020

input Real [:, :] A; //Koefisien Persamaan Linier

input Real [:] B; // Konstanta Ruas Kanan di Persamaan Linier

output Real [:, :] x; //Hasil Perhitungan

protected

Integer m = size(A,1);

Integer n = size(A,2);

Integer c = 0;

Real i = 1;

Real j = 1;

Real k = 1;

Real sum = 1;

Real factor = 1;

Real [:,:] a;

Real [:] b;

algorithm

a := A;

b := B;

for k in 1:(n-1) loop //Forward Elimination dimulai disini

for i in (k+1):n loop

factor := a[i,k] / a[k,k];

for j in (k+1):n loop

a[i,j] := a[i,j] - (factor * a[k,j]);

end for;

b[i] := b[i] - (factor * b[k]);

end for;

end for;

x[n] := b[n] / a[n,n]; //Backward Substitution dimulai disini

for i in (n-1):(-1) loop

sum := b[i];

for j in (i+1):n loop

sum := sum - (a[i,j] * x[j]);

end for;

x[i] := sum / a[i,i];

end for;

end NaiveGauszzRichardo;

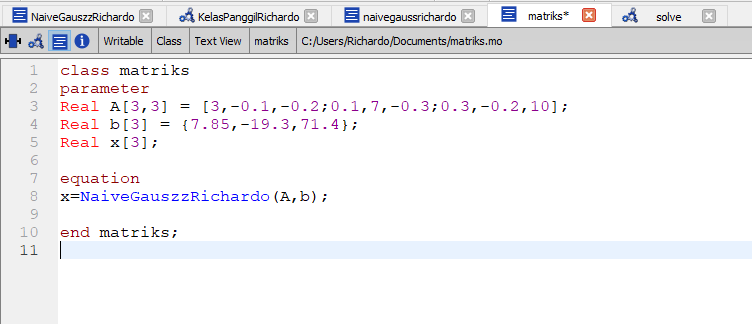
Kemudian saya mencoba menyelesaikan contoh di bagian 9.5 menggunakan kode yang telah saya buat

dan saya membuat kelas panggil untuk mengeksekusi kode yang telah saya buat

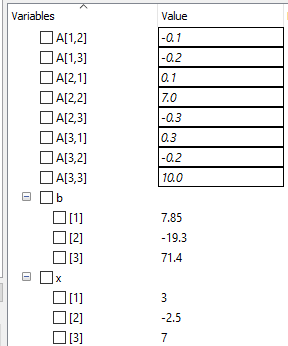
dan setelah saya simulate, saya mendapatkan hasil X1, X2, dan X3 yang sama seperti di buku

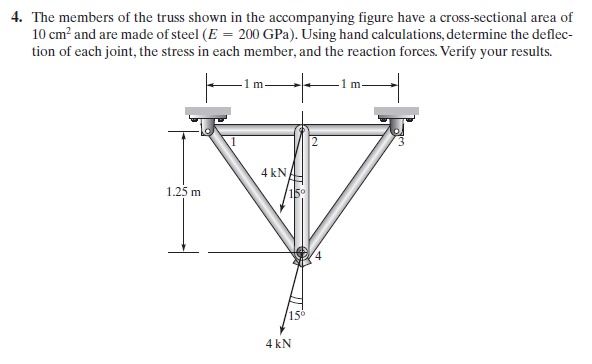
Kemudian saya akan mencoba menyelesaikan tugas yang diberikan dari buku Saeed Moaveni

Berdasarkan soal, diketahui bahwa

• E = 200 GPa
• Luas Cross Section = 10 cm^2
• Jumlah batang = 5

Dalam kesempatan kali ini, saya ingin berterima kasih kepada rekan saya Josiah atas bimbingannya kepada saya dalam menyelesaikan soal ini. Dalam menyelesaikan soal ini kita memerlukan 1 kelas dan 3 fungsi dalam Modelica. Kelas merupakan tempat kita melakukan operasi penghitungan, dan fungsi digunakan untuk:

• Fungsi Matriks Stiffness
• Fungsi Matriks Elemen Global, dan
• Fungsi Matriks Reaksi

Dalam mengerjakan secara manual, ada beberapa tahap yang harus kita lakukan, yaitu

• Memecah permasalahan menjadi Nodes dan elemen
• Mengasumsikan solusi yang dapat mewakili reaksi sistem secara keseluruhan
• Membuat persamaan elemen
• Menggabungkan solusi dari setiap elemen
• Memberikan kondisi dan beban batas
• Kemudian menyelesaikan persamaan dengan metode aljabar linear

Dalam kesempatan kali ini, saya akan langsung menyelesaikan persamaannya dengan menggunakan aplikasi OpenModelica.

• Pertama-tama saya akan membuat kelas pada OpenModelica. Disini kita akan menggabungkan fungsi-fungsi lain dan memberikan kondisi batas untuk memperoleh hasil akhir.

parameter Integer N=8;

parameter Real A=0.001;

parameter Real E=200e9;

Real G[N,N];

Real Ginitial[N,N];

Real Sol[N];

Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};

Real R[N];

Real SolMat[N,1];

Real XMat[N,1];

//Kondisi Batas

Integer b1=1;

Integer b2=3;

//batang 1

parameter Real X1=0; //sudut

Real k1=A*E/1;

Real K1[4,4]; //matriks kekakuan

Integer p1a=1;

Integer p1b=2;

Real G1[N,N];

//batang 2

parameter Real X2=0; //sudut

Real k2=A*E/1;

Real K2[4,4]; //matriks kekakuan

Integer p2a=2;

Integer p2b=3;

Real G2[N,N];

//batang 3

parameter Real X3=90; //sudut

Real k3=A*E/1.25;

Real K3[4,4]; //matriks kekakuan

Integer p3a=2;

Integer p3b=4;

Real G3[N,N];

//batang 4

parameter Real X4=90+38.6598; //sudut

Real k4=A*E/1.6;

Real K4[4,4]; //matriks kekakuan

Integer p4a=1;

Integer p4b=4;

Real G4[N,N];

//batang 5

parameter Real X5=90-38.6598; //sudut

Real k5=A*E/1.6;

Real K5[4,4]; //matriks kekakuan

Integer p5a=3;

Integer p5b=4;

Real G5[N,N];

algorithm

K1:=Stiffness_Matrices(X1);

G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);

G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);

G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);

G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);

G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;

Ginitial:=G;

//kondisi batas

for i in 1:N loop

G[2*b1-1,i]:=0;

G[2*b1,i]:=0;

G[2*b2-1,i]:=0;

G[2*b2,i]:=0;

end for;

G[2*b1-1,2*b1-1]:=1;

G[2*b1,2*b1]:=1;

G[2*b2-1,2*b2-1]:=1;

G[2*b2,2*b2]:=1;

Sol:=Gauss_Jordan(N,G,X);

//menyelesaikan reaksi

SolMat:=matrix(Sol);

XMat:=matrix(X);

R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

• Kemudian saya akan membuat fungsi panggil untuk matriks stiffness

function Stiffness_Matrices

input Real A;

Real Y;

output Real X[4,4];

Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;

X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop

for j in 1:4 loop

if abs(X[i,j]) <= float_error then

X[i,j] := 0;

end if;

end for;

end for;

end Stiffness_Matrices;

• Kemudian adalah fungsi matriks elemen global

function Local_Global

input Real Y[4,4];

input Integer B;

input Integer p1;

input Integer p2;

output Real G[B,B];

algorithm

for i in 1:B loop

for j in 1:B loop

G[i,j]:=0;

end for;

end for;

G[2*p1,2*p1]:=Y[2,2];

G[2*p1-1,2*p1-1]:=Y[1,1];

G[2*p1,2*p1-1]:=Y[2,1];

G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];

G[2*p2-1,2*p2-1]:=Y[3,3];

G[2*p2,2*p2-1]:=Y[4,3];

G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];

G[2*p2-1,2*p1-1]:=Y[3,1];

G[2*p2,2*p1-1]:=Y[4,1];

G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];

G[2*p1-1,2*p2-1]:=Y[1,3];

G[2*p1,2*p2-1]:=Y[2,3];

G[2*p1-1,2*p2]:=Y[1,4];

end Local_Global;

</code>

• Dan fungsi Matriks Reaksi

function Reaction_Trusses

input Integer N;

input Real A[N,N];

input Real B[N,1];

input Real C[N,1];

Real X[N,1];

output Real Sol[N];

Real float_error = 10e-10;

algorithm

X:=A*B-C;

for i in 1:N loop

if abs(X[i,1]) <= float_error then

X[i,1] := 0;

end if;

end for;

for i in 1:N loop

Sol[i]:=X[i,1];

end for;

end Reaction_Trusses;