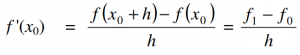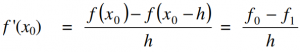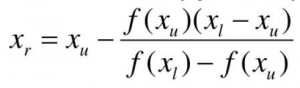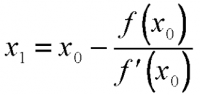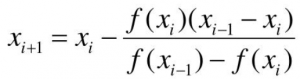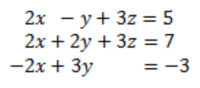Metnum03-Raditya Aryaputra Adityawarman

Raditya Aryaputra

Biodata Diri

Nama: Raditya Aryaputra Adityawarman

NPM:1806181691

Program Studi: S1 Teknik Mesin Paralel

Kelas: Metode Numerik-03

Pertemuan 1: Senin, 9 November 2020

Pada pertemuan pertama setelah UTS, Pak Dai memberikan arahan kepada kami untuk memanfaatkan air.eng.ui.ac.id sebagai bahan untuk belajar. Selain itu, Pak Dai menjelaskan 4 indikator penilaian untuk pembelajaran metode numerik. Indikator pertama adalah memahami konsep dan prinsip. Konsep yaitu gagasa pemikiran mengenai apa saja yang sudah dipelajari, sedangkan prinsip yaitu pemahaman kita dalam memasukkan rumus-rumus. Indikator kedua adalah menerapkan konsep tersebut dalam memecahkan sebuah masalah. Indikator ketiga memahami aplikasi metode numerik ke dalam masalah keteknikan. Indikator yang terakhir adalah nilai tambah dalam mengenal diri kita sendiri sebagai tolak ukur apakah dari pembelajaran metode numerik diri kita bisa berkembang

Materi Sebelum UTS

---

Pada pertemuan sebelum UTS, kami telah belajar 3 materi utama, yaitu turunan numerik, mencari akar-akar, dan membaca pola.

1. Turunan Numerik

turunan numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menentukan turunan:

• Turunan maju

• Turunan mundur

• Turunan pusat

2. Mencari Akar

Pada materi ini, kami belajar cara mencari akar dengan metode numerik. Ada 2 cara dalam mengerjakannya, yaitu bracketing method dan open method.

Bracketing method

Bracketing method adalah metode mencari akar dengan cara menebak dua nilai, kemudian mengurung kedua nilai tersebut sehingga kita dapat menemukan akar-akar dari persamaan. Pada metode ini, ada beberapa cara penyelesaian, yaitu metode graphical, metode bisection, dan false-position.

• Metode Graphical

Metode ini digunakan dengan cara membuat grafik fungsi dan melihat perpotongan sumbu horizontal atau sumbu x.

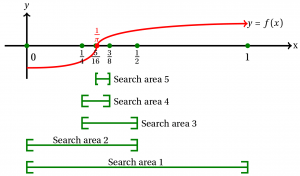
• Metode Bisection

Metode ini dilakukan dengan cara membagi dua kurva yang diwakili oleh suatu titik yang nilainya dikalikan oleh nilai tertinggi dan yang terendah. Metode ini terus dilakukan hingga menemukan akar.

• False Position

Metode ini mirip dengan bisection, namun bedanya untuk penentuan titik tengah menggunakan segitiga dari titik perpotongan kurva dengan garis yang ditentukan.

Open Method

Metode ini hanya menggunakan 1 titik sebagai acuan pertama untuk menemukan akar yang dicari. Open method terbagi menjadi 3 cara, yaitu newton rhapson, secant, dan simple fix point.

• Newton Rhapson

Metode ini dilakukan dengan cara menentukan suatu titik dan menarik garis singgung terhadap kurva. Cara menentukan garis singgung tersebut dengan turunan.

• Secant

Metode ini mirip dengan Newton Rhapson, tapi estimasi dengan 2 titik jika pada newton rhapson f'(x) tidak dapat dicari.

• Simple Fix Point

Metode ini menghitung seluruh kemungkinan x yang dihasilkan dan dicari x konvergen sehingga x=g(x).

3. Membaca Pola

Ada dua cara dalam membaca pola suatu data, yaitu dengan regresi dan interpolasi

• Regresi

• Interpolasi

Tugas 1 Software OpenModelica

---

Saya mempelajari OpenModelica dengan referensi sebagai berikut:

  https://www.youtube.com/watch?v=Dw66ODbMS2A&feature=youtu.be

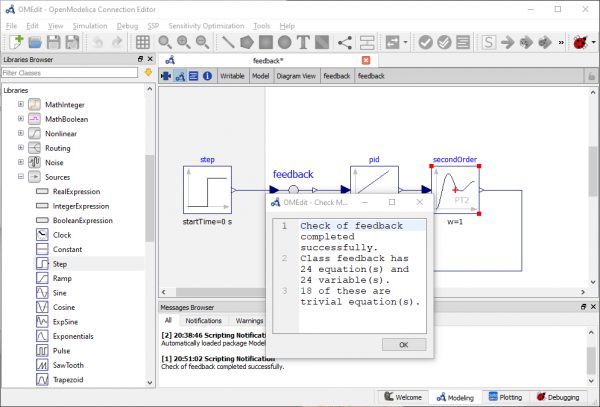
Video tersebut menjelaskan tutorial simulasi feedback control system. Berikut tahapan-tahapan simulasi:

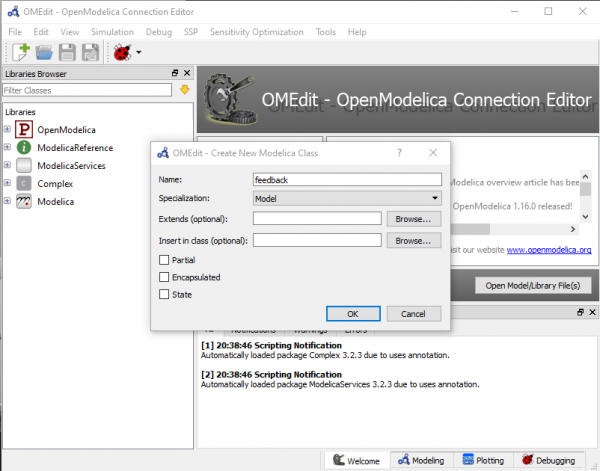
1. Pertama, buka OpenModelica dengan nama feedback
2. Semua diagram blok yang akan disimulasikan terdapat pada tab blocks modelica. Pada simulasi ini, saya menggunakan sistem linear dan simple second order system untuk kontrol.
3. Kemudian saya memakai PID controller pada menu continuous
4. Pilih blok PID dan second order
5. Pada menu math, pilih blok feedback
6. Pada menu sources, pilih step sebagai input
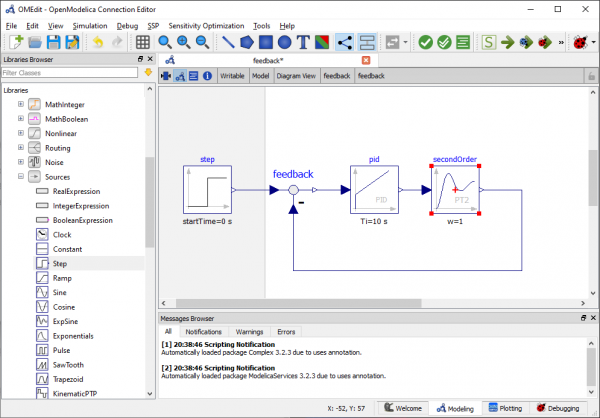
7. Setelah itu, blok-blok tersebut dihubungkan dengan cara menarik garis antar blok sehingga sistem menjadi closed loop
8. Kemudian mengatur parameter yang diinginkan. Sistem tersebut underdamped, sehingga nilai damping yang dimasukkan <0.7
9. Cek model apakah sudah siap untuk diset up atau belum
10. Setelah siap untuk disimulasikan, kita menyimpan terlebih dahulu pada tempat default
11. Jalankan simulasi dan tunggu hingga selesai
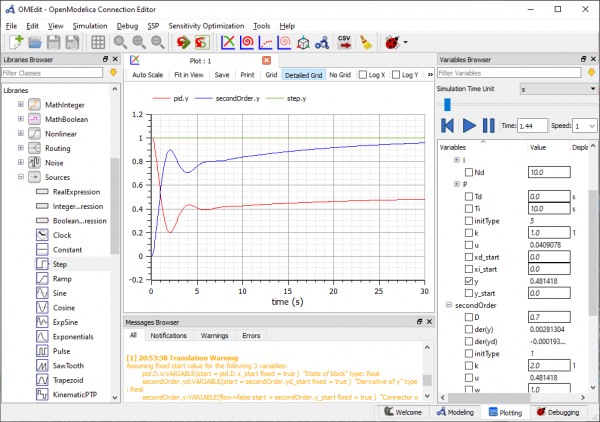
12. Setelah simulasi selesai dilakukan, untuk melihat kurva centang y pada PID, step, dan second order
13. Hasil simulasi didapatkan. Kita bisa mengubah parameter sehingga hasil simulasi lebih jelas

Lampiran

---

membuat file

diagram blok

cek blok sebelum simulasi

hasil simulasi

Pertemuan 2: Senin, 16 November 2020

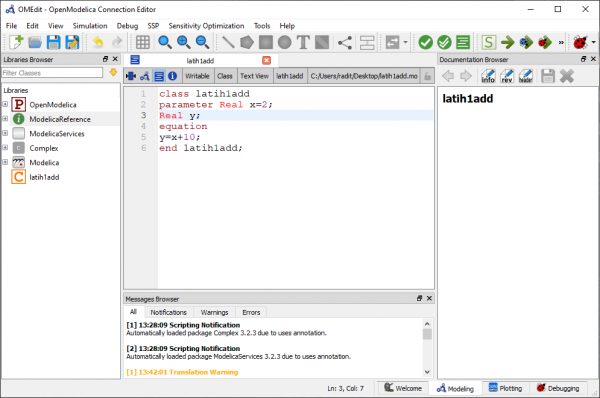
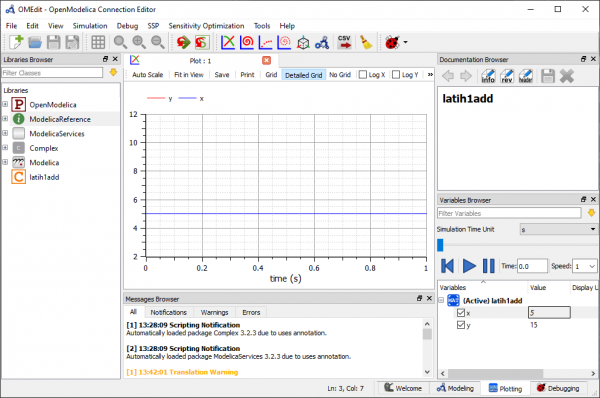
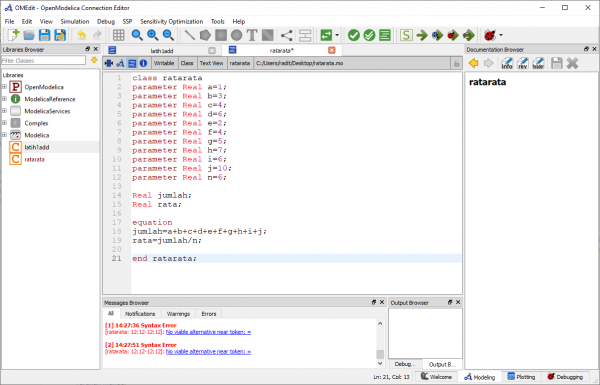
Pada pertemuan ini, Pak Dai meminta setiap mahasiswa menunjukkan tugas minggu lalu, yaitu belajar OpenModelica. Lalu kami simulasi membuat program sederhana didalam modelica untuk menjumlahkan angka 10 kepada sebuah variabel. Berikut parameter dan hasilnya:

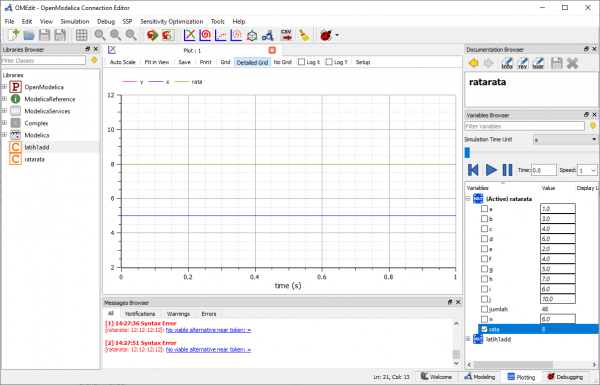
Lalu kami diminta untuk membuat program untuk mencari nilai rata-rata. Berikut parameter dan hasilnya:

Tugas 2 Menyelesaikan Aljabar Simultan

---

Pada tugas ini saya menggunakan persamaan berikut untuk mengerjakan tugas 2.

Dalam hal ini, bisa dilakukan beberapa metode dalam mengerjakannya, seperti menggunakan eliminasi gauss, gauss jordan, crammer, dan gauss seidel.

• Eliminasi gauss adalah suatu tahapan untuk memecahkan persamaan dengan cara mereduksi / menyederhanakan matriks persamaan tersebut. Prosedur dalam metode Gauuss akan menghasilkan bentuk matrik pada eselon tereduksi.
• Gauss jordan merupakan pengembangan metode eliminasi Gauss, hanya saja augmented matrik, pada sebelah kiri diubah menjadi matrik diagonal.
• Metode Cramer menggunakan determinan suatu matriks dan matriks lain yang diperoleh dengan mengganti salah satu kolom dengan vektor yang terdiri dari angka di sebelah kanan persamaannya.
• Gauss seidel digunakan untuk menyelesaikan sistem persamaan linear (SPL) berukuran besar dan proporsi koefisien nolnya besar, seperti sistem-sistem yang banyak ditemukan dalam sistem persamaan diferensial.

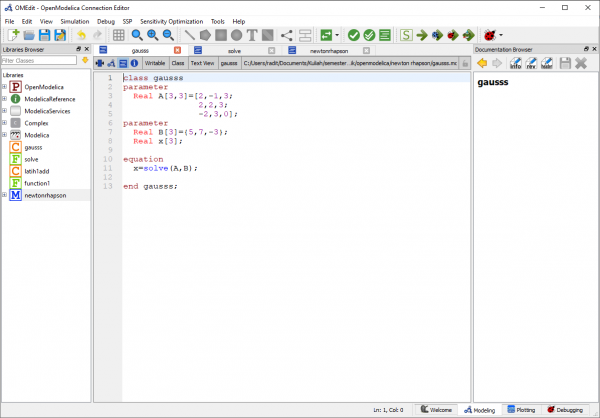
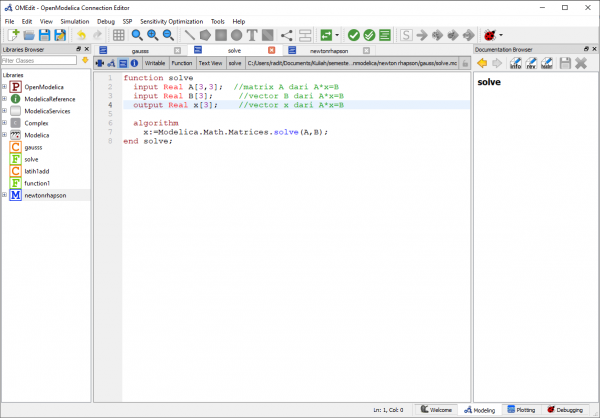
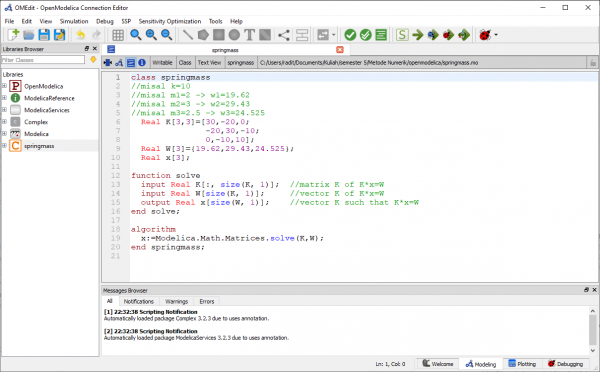
Pada tugas ini, saya memakai metode eliminasi gauss dalam menyelesaikannya. Berikut percobaan yang saya lakukan:

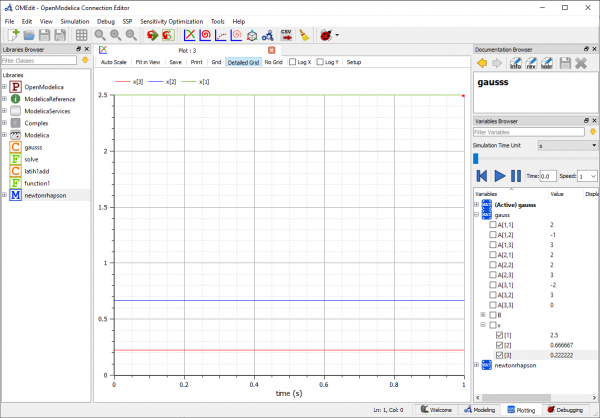
Dari simulasi ini didapatkan hasil x=2.5, y=0.66667, dan z=0.22222

Referensi dari percobaan di atas didapat dari https://build.openmodelica.org/Documentation/Modelica.Math.Matrices.solve.html.

---

Selain itu, saya mencoba membuat persamaan Newton Rhapson. Metode ini dilakukan dengan cara menentukan suatu titik dan menarik garis singgung terhadap kurva. Cara menentukan garis singgung tersebut dengan turunan. Kelebihan dari metode ini adalah hasilnya didapatkan dengan cepat, hanya memerlukan satu titik saja, dan caranya sederhana. Namun, kekurangan dari metode ini adalah tidak semua persamaan konvergen sehingga beberapa persamaan tidak mempunyai solusi dengan metode ini. Selain itu ketika memilih titik yang turunannya=0, cara ini tidak bisa digunakan.

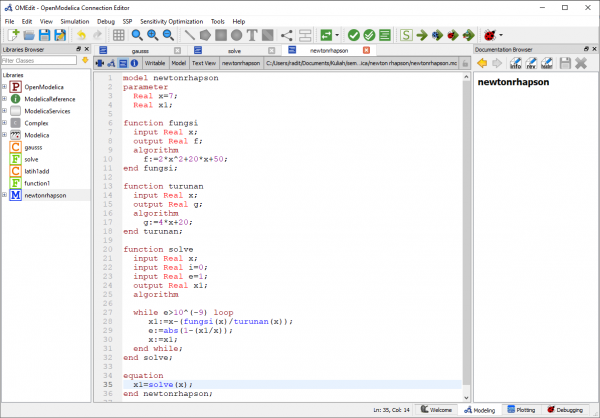
Pertama-tama saya membuat fungsi pada function. Persamaan yang saya gunakan yaitu y=2x^2+20x+50. Selanjutnya, saya membuat fungsi turunan dengan persamaan y'=4x+20.

Kemudian saya membuat rumus newton rhapson pada function solve. Rumusnya yaitu Xn=(xn-1)-(f(xn-1)/f'(xn-1)). Input yang dimasukkan x0, i=0, dan x1. X sebagai variabel yang dimasukkan. Sementara i merupakan iterasi. Saya menggunakan loop while, sehingga program terus melakukan looping selama error lebih besar dari 10^-9.

Lalu saya membuat equation. Equation ini untuk menghitung fungsi-fungsi yang sudah dibuat. Parameternya yaitu x0=7 dan x1. x0=7 merupakan titik yang ditentukan.

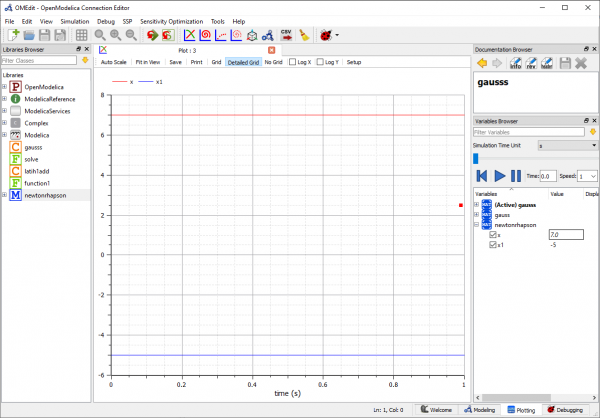
Setelah dilakukan simulasi, maka didapatkan hasil dari persamaan y=2x^2+20x+50 yaitu titik yang memotong garis horizontal x=-5.

Pertemuan 3: Senin, 23 November 2020

Pada pertemuan ini, kami diminta untuk menjelaskan tugas minggu lalu, yaitu penyelesaian aljabar simultan. Selain itu, Pak Dai menjelaskan aplikasi metode numerik dalam permasalahan teknik. Urutan penyelesaiannya yaitu:

1. masalah teknik, yaitu tahapan membuat gambaran mengenai masalah yang ada, seperti parameter dan metode yang digunakan.
2. analisis masalah, yaitu respon dari kasus yang ada. Pada tahap ini menganalisis permasalahan dari parameter-parameter yang sudah diketahui
3. model matematis, membuat model matematika dari variabel yang ada dengan hukum fisika.
4. model numerik, yaitu menggunakan bahasa pemrograman untuk menyelesaikan permasalahan yang ada, contohnya menggunakan open modelica untuk menyelesaikan aljabar simultan.
5. komputer, yaitu menggunakan software untuk menyelesaikan perhitungan, seperti open modelica, cfdsof, mathlab, dll.
6. solusi, hasil dari simulasi didapatkan.

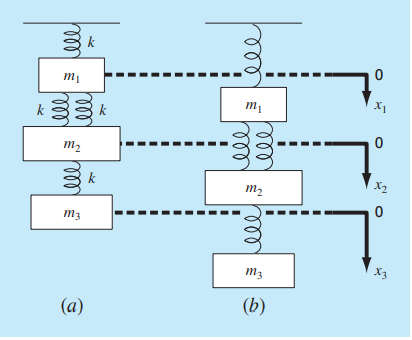
Selanjutnya Pak Dai memberi tugas untuk menyelesaikan permasalahan pegas massa yang terdapat pada bab 12 dari buku Numerical Method. Berikut soalnya:

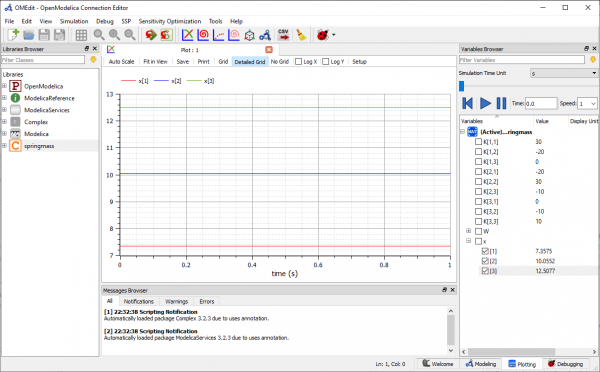
Untuk menyelesaikan soal ini, pertama-tama membuat free body diagram dari masing-masing sistem. Kemudian menuliskan persamaannya. Setelah itu, persamaan tersebut dapat diselesaikan dengan metode numerik, yaitu membuat matriks dan diselesaikan dengan eliminasi gauss. Berikut kode yang digunakan:

Berikut hasilnya, di mana x1 = 7,36, x2 = 10,06, x3 = 12,51