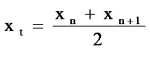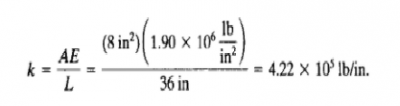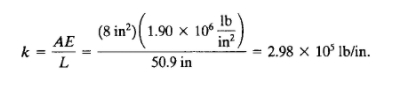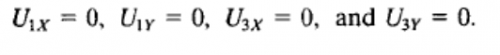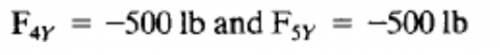Metnum03 Bhismantyo Tsaqif Daniswara
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
Biodata Diri
Nama : Bhismantyo Tsaqif Daniswara
NPM : 1806181754
Program Studi : S1 Pararel Teknik Mesin
Pertemuan 01
Pada pertemuan pertama ini, Pak Dai menjelaskan dan mengarahkan mengenai pelajaran Metode Numerik sebelum UTS. Pada page ini, saya akan menjelaskan apa yang sudah saya pelajari mengenai Metode Numerik.
Metode untuk mencari akar-akar persamaan
1. Metode Tertutup
a. Metode Biseksi
Metode Biseksi memiliki beberapa langkah-langkah penyelesaian sebagai berikut :
1.Hitung fungsi pada interval yang sama dari x sampai pada perubahan tanda dari fungsi f(xn) dan f(xn+1), yaitu :f(xn) . f(xn+1) < 0 2.Estimasi pertama dari akar xt dihitung dengan
3.Buat evaluasi berikut untuk menentukan di dalam sub interval mana akar persamaan berada : a.f(xn).f(xt) < 0, akar persamaan berada pada sub interval pertama, kemudian tetapkan xn+1 = xt dan lanjutkan pada langkah ke-4 b.f(xn).f(xt) > 0, akar persamaan berada pada sub interval kedua, kemudian tetapkan xn = xt dan lanjutkan pada langkah ke-4 c.f(xn).f(xt) = 0, akar persamaan adalah xt dan hitungan selesai 4.Hitung perkiraan baru dari akar dengan
5.Apabila perkiraan baru sudah cukup kecil (sesuai dengan batasan yang ditentukan), maka hitungan selesai, dan xt adalah akar persamaan yang dicari. Jika belum, maka hitungan kembali ke langkah ke-3
b. Metode Regulasi Falsi
Metode Regula Falsi didasarkan pada interpolasi antara dua nilai dari fungsi yang mempunyai tanda berlawanan. Metode regulasi falsi memiliki langkah-langkah sebagai berikut :
1.Hitung fungsi pada interval yang sama dari x sampai pada perubahan tanda dari fungsi f(xn) dan f(xn+1), yaitu f(xn) . f(xn+1) < 0 2.Mencari nilai x* dengan persamaan :
3.Nilai tersebut digunakan untuk menghitung nilai f(x*), yang kemudian digunakan lagi untuk interpolasi linier dengan nilai f(xn) atau f(xn+1) sedemikian sehingga kedua fungsi mempunyai tanda berbeda. 4.Prosedur diulang lagi sampai didapat nilai f(x*) mendekati nol
2. Metode Terbuka
a. Metode Newton Raphson
Metode Newton Raphson memiliki langkah-langkah sebagai perikut:
1.Pilih nilai awal xi sembarang 2.Hitung xi+1 dan f (xi+1) dengan rumus :
3.Demikian seterusnya sampai didapatkan f (xi+1) yang kecil
b. Metode Secant
Kekurangan Metode Newton Raphson adalah diperlukannya turunan pertama (differensial) dari f(x) dalam hitungan. Kadang-kadang sulit untuk mendiferensialkan persamaan yang diselesaikan. Untuk itu maka bentuk diferensial didekati dengan nilai perkiraan berdasarkan diferensial beda hingga.
Dalam metode ini pendekatan memerlukan dua nilai awal dari x
c. Metode iterasi
Dalam metode iterasi ini digunakan suatu persamaan untuk memperkirakan nilai akar persamaan. Persamaan tersebut dikembangkan dari fungsi f(x) = 0 sehingga parameter x berada disisi kiri dari persamaan, yaitu :
x= g(x)
Persamaan ini menunjukkan bahwa nilai x merupakan fungsi dari x, sehingga dengan memberi nilai perkiraan awal dari akar dapat dihitung perkiraan baru dengan rumus iteratif berikut :
Besar kesalahan dihitung dengan rumus berikut :
Pemahaman Modelica
Lampiran :
Link Video : https://youtu.be/nZLv1rvAdu8
Pertemuan 02
Pada pertemuan ini, Pak Dai kembali menjelaskan mengenai program OpenModelica. Pada pertemuan ini Pak Dai memberi tugas yaitu menyelesaikan persamaan aljabar dengan metode Gauss Jordan, pada aplikasi OpenModelica ini.
1. Membuat Formula
Pada tahap ini, saya terlebih dahulu membuat formula yang akan diproses oleh OpenModelica.
2. Check Formula
3. Hasil Simulation
didapat hasil x = 26, y = -2, z = -8
Pertemuan 03
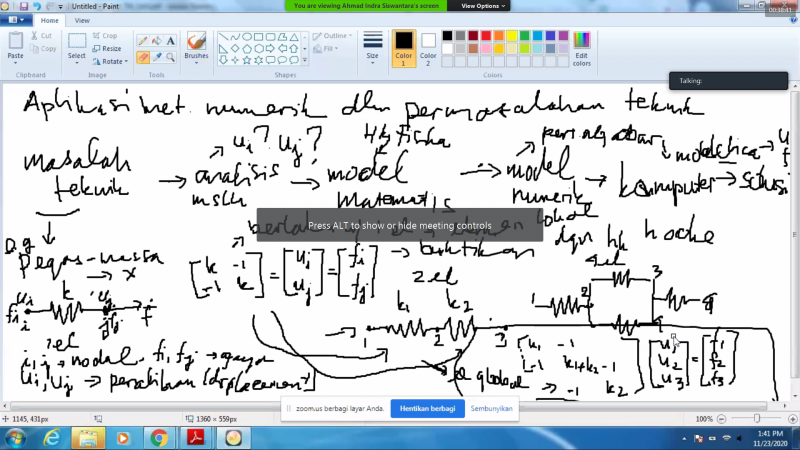
Pada Pertemuan ini, Pak Dai menjelaskan mengenai bagaimana aplikasi metode numerik dalam permasalahan teknik.
Step : Masalah teknik - Analisis masalah - Model Matematis - Metode Numerik - Komputer - Solusi
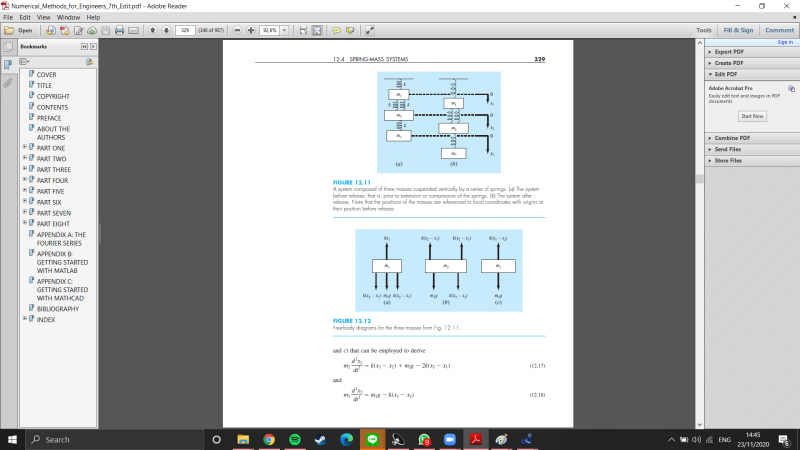
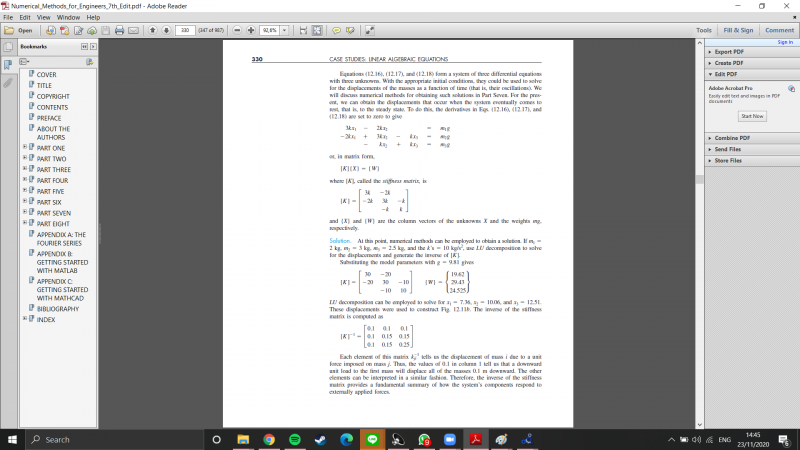
Pada pertemuan ini, Pak Dai menugaskan kami untuk mencoba menyelesaikan permasalahan pegas 12.11 pada buku "Numerical Methods for Engineers 7th Edition"
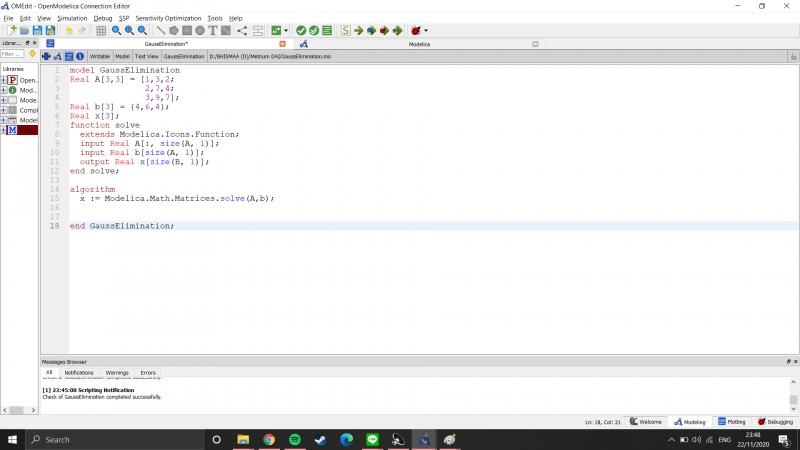
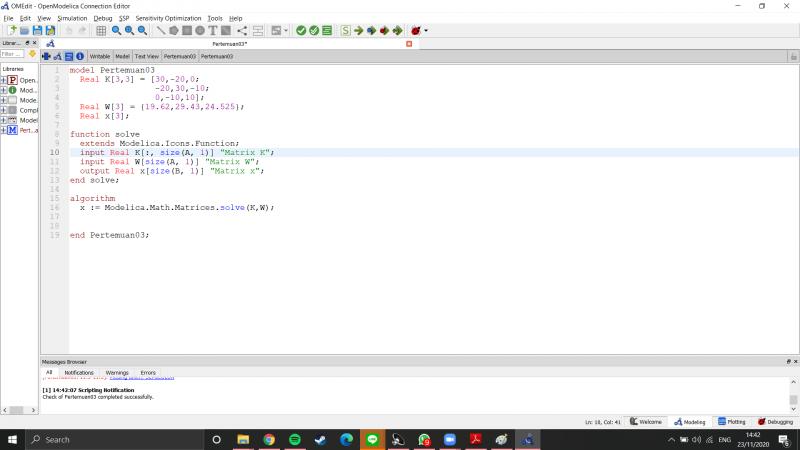
Setelah itu, saya memasukan rumus matrix yang tertera pada buku ke dalam aplikasi OpenModelica
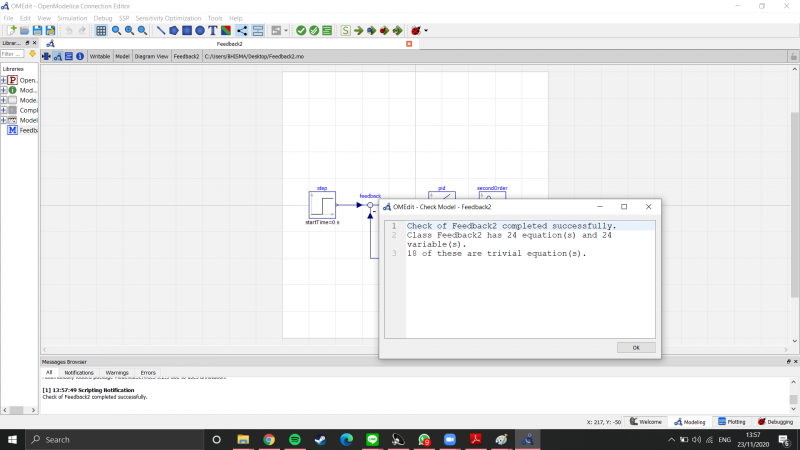
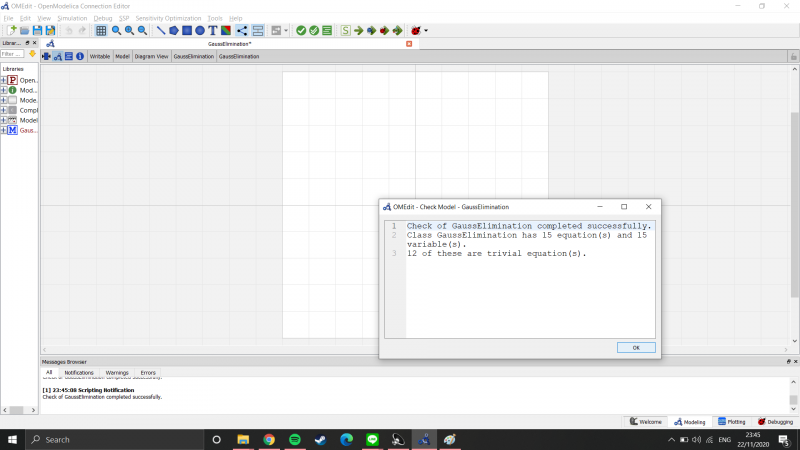
Setelah itu sebelum masuk ke simulasi, saya check formula saya terlebih dahulu
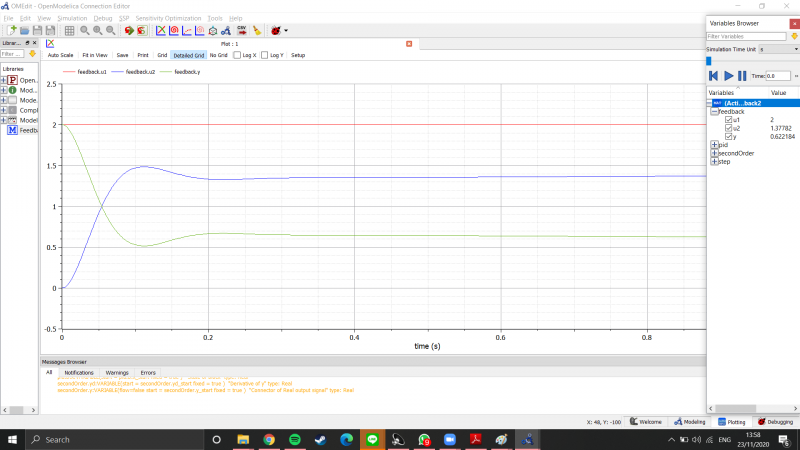
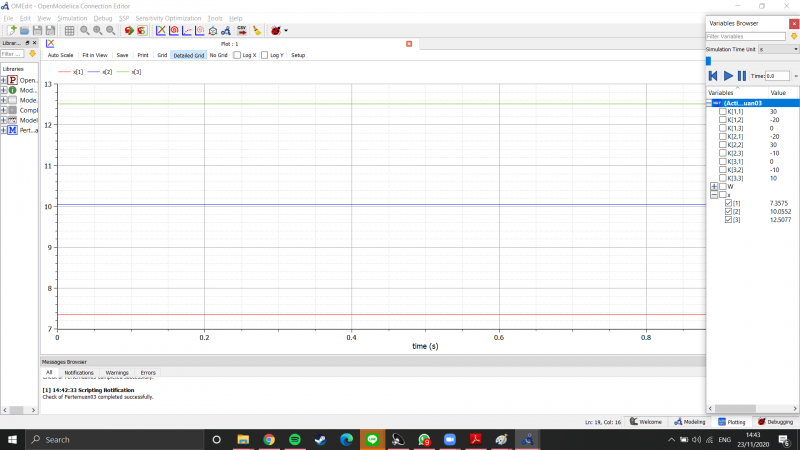
Setelah itu, baru saya simulasi untuk mendapatkan jawaban dari permasalahan tersebut
Didapatkan hasil : x1 = 7.357, x2 = 10.055, x3 = 12.507
Setelah itu, Pak Dai menugaskan kami untuk mengerjakan PR yakni :
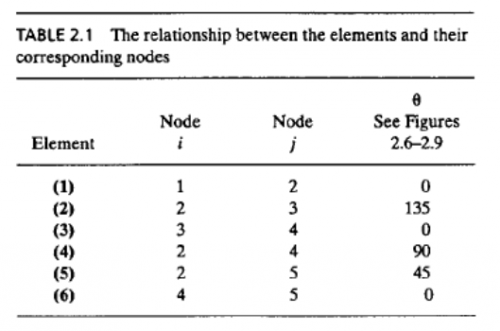
1. Mengubah problem menjadi node
2. Menentukan Konstanta
a. Elemen 1,3,4,6
b. Elemen 2,5
3. Membuat matriks elemen
a. Analisis Elemen 1,3,6
b. Analisis Elemen 4
c. Analisis Elemen 2,5
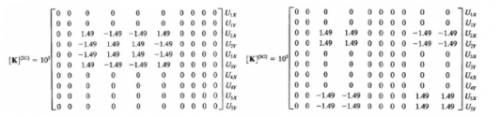
4. Menyusun matriks elemen
5. Menerapkan batas
a. node 1 dan 3 Fixed
b. External Force 4 dan 5
Dengan Hukum Hooke, diadapat matriks :