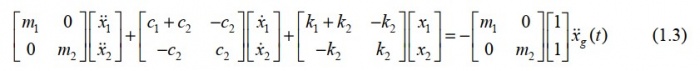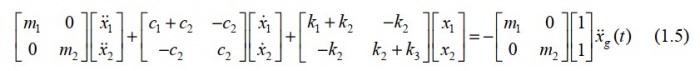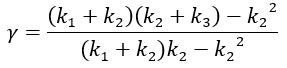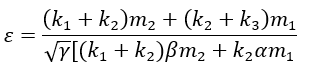Using Spring-Mass Models to Determine the Dynamic Response of Two-Story Buildings Subjected to Lateral Loads by S.T. De la Cruz, M.A. Rodríguez & V. Hernández

<- back to Studi kasus komputasi teknik

Case Study

Terjemahan

1. Pengantar

Model mekanis struktur dapat diwakili oleh sistem massa pegas (Brennan et al., 2008; Delhomme et al., 2007; Wu, 2004). Ketika berhadapan dengan struktur bangunan yang terkena beban gempa, single-story buildings (SSB) dan multi-story buildings (MSB) juga dapat diwakili oleh spring-mass models (SMM) (De la Cruz dan López-Almansa, 2006; Wilkinson dan Thambiratnam, 2001).

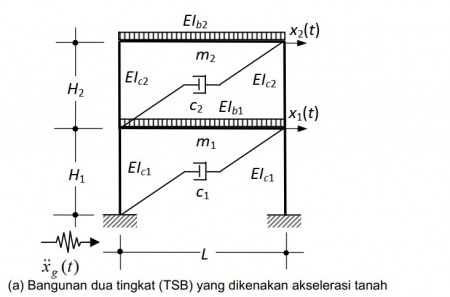
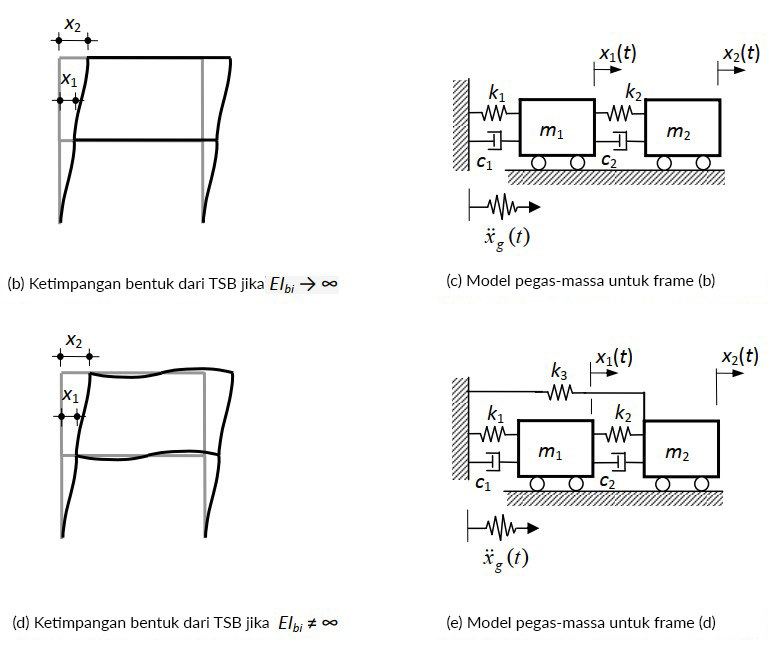
Sebagai contoh, pada Gambar. 1.1a SSB ditampilkan. Panjang gelagar (beam) diwakili oleh L dan ketinggian bingkai (frame) diwakili oleh H. Jika kekakuan lentur gelagar, diwakili oleh EIb, sangat kaku, bentuk terdistorsi SSB ketika mengalami percepatan tanah x (t) g ditunjukkan pada Gambar. 1.1b, di mana koordinat horisontal x berarti tingkat kebebasan bingkai tunggal.

SMM yang sesuai digambarkan pada Gambar 1.1c. Kuantitas m, c dan k, masing-masing, massa gelagar, redaman kental SSB dan kekakuan keseluruhan SSB. Dalam hal ini, kekakuan k ini adalah fungsi dari kekakuan lentur, EIc, dari kedua kolom, dan ketinggian H. Di sisi lain, jika EIb tidak lagi kaku secara tak terbatas, gerakan diasumsikan dari SSB ditunjukkan pada Gambar. 1.1d, dan SMM-nya ditunjukkan pada Gambar. 1.1e. Dalam hal ini, kekakuan aktual k 'adalah fungsi dari kedua kekakuan lentur, EIb dan EIc, dan panjang L dan tinggi H.

Persamaan gerak model yang ditunjukkan pada Gambar. 1.1c adalah sebagai berikut:

 

di mana titik atas mewakili turunan waktu x. Persamaan gerak model yang ditunjukkan pada Gambar. 1.1e adalah Persamaan yang sama. (1.1) asalkan kekakuan aktual k 'akan menggantikan k.

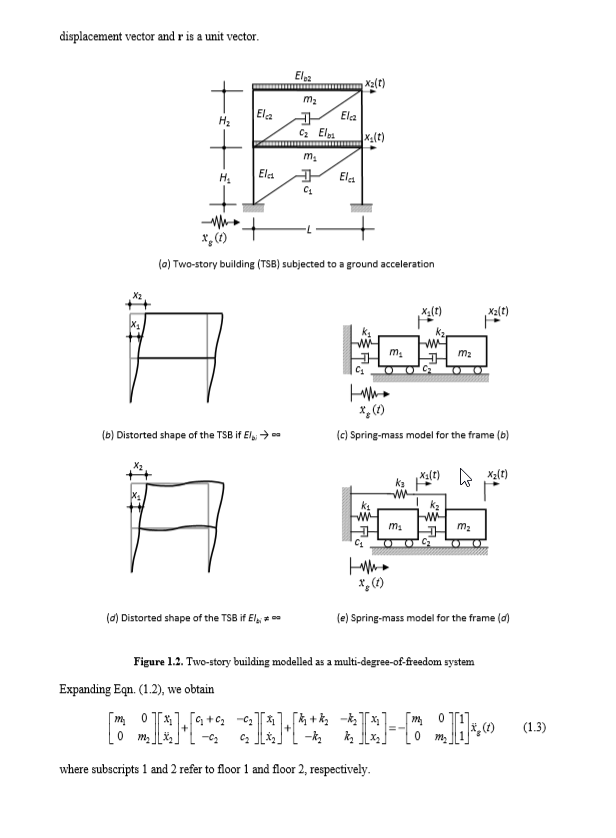
Gambar 1.2. Bangunan dua lantai dimodelkan sebagai sistem multi-derajat-kebebasan

Memperluas persamaan (1.2), kita mendapatkan:

di mana subskrip 1 dan 2, masing-masing merujuk ke lantai 1 dan lantai 2. Di sisi lain, persamaan gerak model yang ditunjukkan pada Gambar. 1.2e adalah

memperluas persamaan (1.4), kita mendapatkan

Matriks kekakuan yang baru, 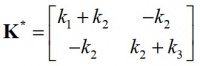umumnya diperoleh setelah membuat kondensasi matriks statis (Cheng, 2001). Perhatikan bahwa Persamaan. (1.2) tidak lagi valid untuk model yang ditunjukkan pada Gambar. 1.2e karena matriks kekakuan keseluruhan K* dalam Persamaan (1.4) diperoleh dengan menambahkan koefisien kekakuan baru ke matriks K.

Sebagai catatan terakhir dari pengantar ini, kita tahu bahwa untuk SSB kedua kondisi ('shear building’, SB, dan ‘moment resistant frame‘, MRF) dapat direpresentasikan untuk persamaan gerak yang sama ―Eqn. (1.1)- karena kekakuan dari keseluruhan sistem, k, dapat dimodifikasi untuk memasukkan derajat kebebasan lateral dan rotasi dari simpul (De la Cruz dan López-Almansa, 2006). Untuk TSB, bagaimanapun, modifikasi serupa tidak dapat dilakukan karena kita berurusan dengan matriks kekakuan, alih-alih koefisien tunggal, yang merupakan kasus SSB.

Makalah ini membahas prosedur untuk mendapatkan respon dinamis dari Bangunan dua lantai (TSB) (baik SB atau MRF) yang diwakili oleh SMM ketika mengalami kekuatan lateral (mis., Angin, gempa bumi).

2. Pengembangan

2.1. Bangunan Dua Lantai (TSB)

Bangunan Dua Lantai (TSB) yang ditunjukkan pada Gambar. 1.2a akan dipertimbangkan untuk analisis ini. Seperti yang sudah terlihat, ketika kekakuan dari gelagar (EIb)i , pendekatan hingga tak terbatas, diasumsikan bentuk bingkai yang terdistorsi ditunjukkan pada Gambar. 1.2b, SMM-nya digambarkan pada Gambar. 1.2c dan persamaan gerak sama dengan Eqn. (1.2). Sekarang, mempertimbangkan kekakuan lentur dari kedua balok utama dan kolom, bentuk bingkai yang terdistorsi adalah digambarkan pada Gambar. 1.2d, SMM-nya ditunjukkan pada Gambar. 1.2e dan persamaan gerak sama dengan Eqn. (1.4).

Koefisien kekakuan k2 + k3 dari kekakuan matriks K* membuat sulit untuk membangun fisik model TSB sebagai istilah k3 dapat berupa positif atau negatif (De la Cruz dan López-Almansa, 2006). Kasus terakhir yaitu k3<0, sarana untuk memasang pegas dengan kekakuan negatif massa m2. Dalam kasus ini sebuah prosedur dikembangkan untuk menangani kemungkinan jika k3 bernilai positif atau negative.

2.2. Konstruksi Model Massa Pegas Setara

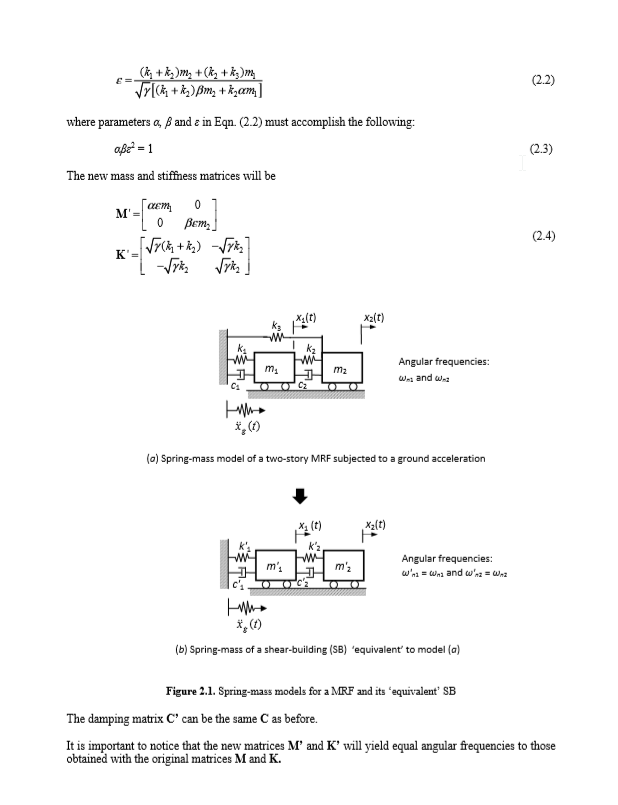
Dimungkinkan untuk membangun SB 'setara' dengan MRF menggunakan model pegas-massa, asalkan frekuensi sudut ωn1 dan ωn2 dari model baru sama dengan frekuensi dari model asli. Gambar 2.1 menggambarkan penegasan ini.

Untuk mengkonversi model Gambar 2.1b yang matriks-matriks barunya adalah M', C' dan K' menjadi model Gambar 2.1a , yang matriks aslinya adalah M, C dan K *, perlu untuk menentukan parameter γ dan ε sebagai berikut:

(2.1)

(2.2)

3. Applicaiton

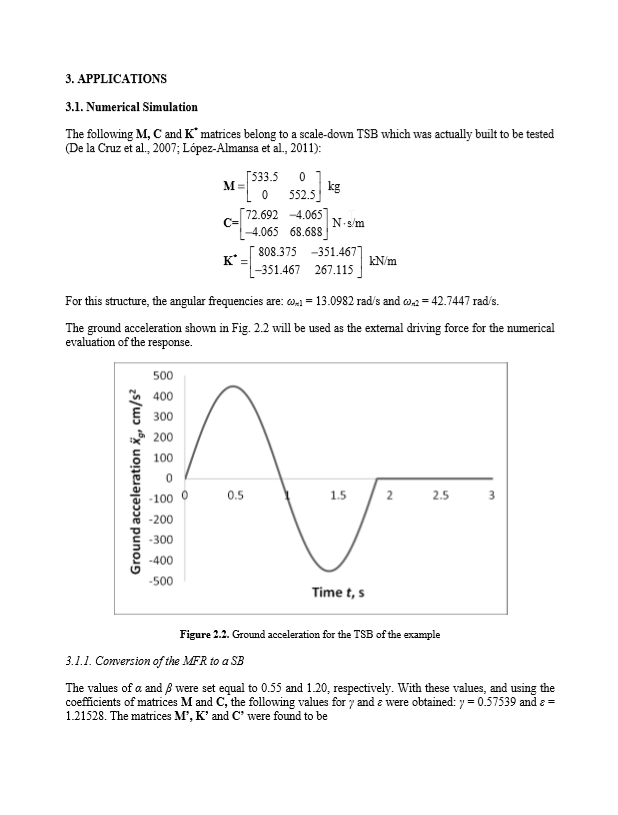
Matriks M, C dan K * berikut milik TSB skala-turun yang sebenarnya dibangun untuk diuji

Untuk struktur ini, frekuensi sudutnya adalah ωn1 = 13.0982 rad/s and ωn2 = 42.7447 rad/s.

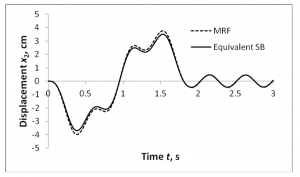
Akselerasi ground yang ditunjukkan pada Gambar 2.2 akan digunakan sebagai kekuatan pendorong eksternal untuk evaluasi numerik dari respons.

3.1.1. Konversi MFR ke SB

Nilai α dan β ditetapkan masing-masing sebesar 0,55 dan 1,20. Dengan nilai-nilai ini, dan menggunakan koefisien matriks M dan C, nilai-nilai berikut untuk γ dan ε diperoleh: γ = 0,57539 dan ε = 1,21528. Matriks M ’, K’ dan C ’ditemukan.

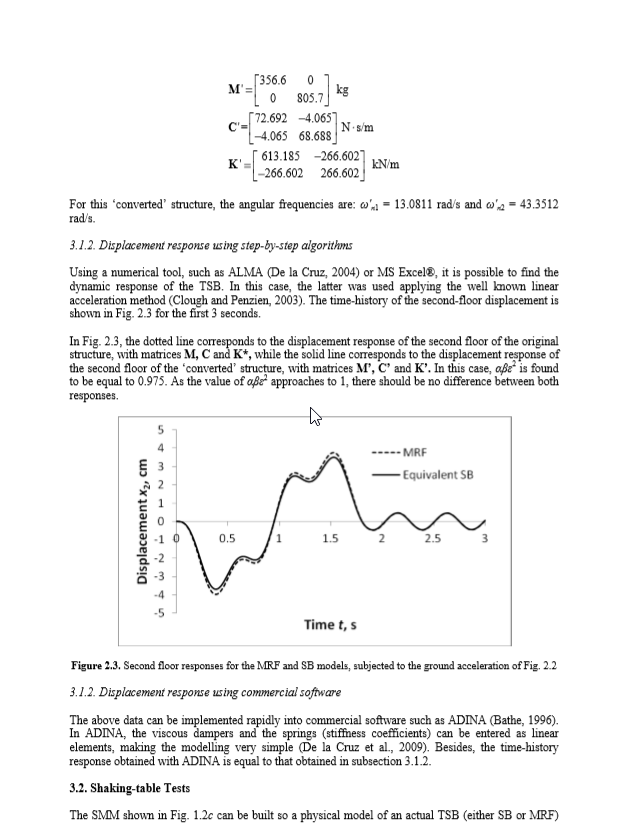
Untuk struktur 'yang dikonversi' ini, frekuensi sudutnya adalah: ω'n1 = 13.0811 rad / s dan ω'n2 = 43.3512 rad / s

3.1.2

3.1.2. Respons Perpindahan Menggunakan Merangkat Lunak Komersial

Data di atas dapat diimplementasikan dengan cepat ke dalam perangkat lunak komersial seperti ADINA (Bathe, 1996). Di ADINA, peredam viskos dan pegas (koefisien kekakuan) dapat dimasukkan sebagai elemen linier, membuat pemodelan sangat sederhana (De la Cruz et al., 2009). Selain itu, sejarah waktu respons yang diperoleh dengan ADINA sama dengan yang diperoleh pada ayat 3.1.2.

3.2. Pengujian Meja Goyang

SMM ditunjukkan pada Gambar. 1.2c dapat dibangun sehingga model fisik dari TSB yang sebenarnya (baik SB atau MRF) dapat diuji. Selain itu, perilaku nonlinear (mis., Kekakuan bi-linear) dapat disimulasikan dengan menggunakan perangkat gesekan yang melekat pada mata air (De la Cruz et al., 2010).