Raymond Lesmana

AKAL

Terdapat 2 dosen pengajar di kelas Metode Numerik ini yaitu Dr. Ahmad Indra Siswantara alias Aki Dai dan Dr. Gunawan. Beliau memberitahukan kepada kami mengenai 2 tujuan utama dari kelas Metode Numerik ini. Tujuan kelas ini adalah :

A. Mehamami konsep / prinsip dan mampu menenerapkannya

B. Menjadi orang yang lebih mengenal siapa dirinya

Dari kedua tujuan yang dipaparkan oleh beliau, hal yang menjadi prasyaratnya adalah BERAKAL. Manusia diberkahi dengan akal budi dari Tuhan Yang Maha Esa. Orang yang berakal adalah orang yang dapat membedakan mana yang benar dan salah. Dengan berakal sudah sepatutnya manusia menjadi pribadi yang baik dan bijaksana dalam konteks berpikir ataupun bertindak. Aki Dai berkata bahwa matematika adalah hal yang dapat memberikan jawaban dan sekaligus dapat menyesatkan. Tidak sedikit ilmuwan kelas dunia yang berubah menjadi atheis dikarenakan oleh pengetahuan yang dimilikinya. Hal ini yang disebutkan oleh Aki Dai sebagai matematika dapat menyesatkan kita.

Metode Numerik

Dalam perkuliahan yang dilakukan ini ada 5 langkah pembelajaran untuk dapat memahami dan menguasai mata kuliah ini secara maksimal. Langkah tersebut sebagai berikut :

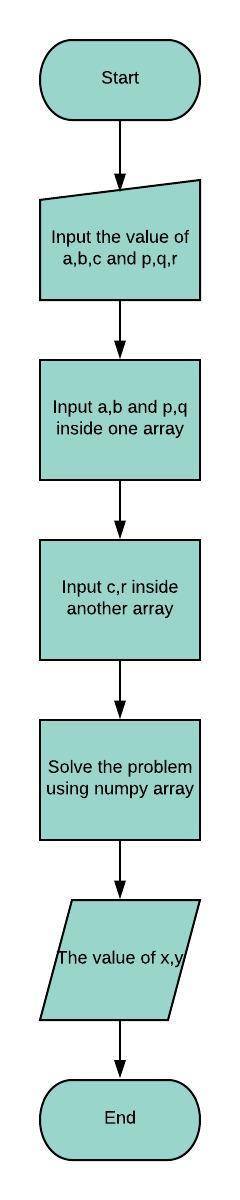
1. Algoritma, Flowchart, Pemograman, Metode iterative

2. Penyelesaian Persamaan-Persamaan Aljabar Simultan

3. Differensial dan Integral

4. Optimasi

5. Studi Kasus

Dari langkah-langkah pembelajaran di atas, kita sudah sepatutnya memahami betul mengenai persamaan aljabar simultan, differensial, dan integral di mata kuliah kalkulus yang sudah kita ambil sebelumnya. Mengapa hal tersebut sangatlah penting di mata kuliah ini karena untuk mengoptimasi sebuah keadaan atau kasus yang berhubungan dengan engineering untuk mendapatkan output maksimum dengan input minimum perlu dibuat sebuah perhitungan matematis yang dapat mendefinisikan dan mencari solusi dari masalah yang ada. Contoh untuk menghitung Stress ataupun tegangan yang ada kita perlu melalui perhitungan seperti ini :

ΣF = 0

Dσ = 0

dengan melakukan penurunan rumus seperti halnya diatas kita dapat menentukan dan mengetahui tegangan yang ada lalu kita dapat mengoptimasikan bagaimana pengaturan tegangan yang terbaik. Optimasi ini dilakukan dengan komputer karena kecepatan perhitungan atau komputasinya yang dapat memberikan solusi terbaik dari berbagai keadaan dan percobaan yang ada dengan kurun waktu yang cepat dikarenakan komputer dapat menghitung lebih cepat dari manusia. Kita mempelajari algoritma, flow chart, dan pemograman di mata kuliah sehingga kita mengetahui bagaimana komputer tersebut mengeksekusi sebuah sistem yang ada dan kita dapat mengerti bahasa pemograman sehingga kita dapat menuangkan apa yang kita mau lewat aplikasi yang kita buat.

Studi Kasus

Aki Dai mengajak kita berpikir mengenai persoalan matematis yang ada. Beliau memberikan contoh soal sebagai berikut :

Apabila kita langsung memasukan x = 1, maka perhitungan yang didapat ialah 0/0 atau tidak terdefinisi. Menurut beliau, 0/0 bukanlah terdefinisi namun hanya Tuhan yang tahu jawabannya dan kita manusia tidak sampai kesana. Solusi yang dapat kita lakukan adalah melakukan penurunan sehingga didapat bahwa hasilnya adalah 2. Namun Aki Dai meminta kita untuk berpikir lebih dalam, dan salah seorang teman kami memnjawab persamaan itu tidak dapat diselesaikan begitu saja karena titik x = 1 tidak ada pada fungsi yang tersebut sehingga dilakukan pendekatan yang menggunakan limit. Cara berpikir yang logis dan matematis diperlukan untuk menyelesaikan permasalahan-permasalahan yang ada terutama pada mata kuliah Metode Numerik ini sehingga mata kuliah ini dapat menjadi bekal kita untuk semakin berkembang dan berpikir layaknya seorang engineer.

Pertemuan 2

Metode Numerik yang dilakukan mempermudah kita sebagai calon engineer untuk melakukan perhitungan dengan cepat. Oleh karena itu, banyak permasalahan di dunia yang dapat ditulis dalam rumus matematis dapat kita lakukan perhitungan dengan menggunakan metode numerik demi mendapat nilai yang paling ideal. Optimasi juga dapat dilakukan guna untuk mendapat nilai terbaik atau hasil terbaik dengan waktu yang singkat.

Kasus yang dapat diselesaikan dengan persamaan matematis

1. Optimasi bentuk propeller sehingga propulsi yang dihasilkan seoptimal mungkin

2. Optimasi peletakan kamar mesin sehingga tenaga yang dihasilkan lebih terjaga

PR

Perintah :

1. Cetak ax +by = c dan px +qy=r

2. Cetak masukan nilai a,b,c dan p,q,r

3. Input nilai a,b,c dan p,q,r

4. Taruh nilai a,b dan p,q ke dalam satu matrix

5. Taruh nilai c dan r ke dalam matrix lainnya

6. Lakukan perhitungan dengan menggunakan numpy linear algebra

7. Cetak hasil x dan y

Flowchart :

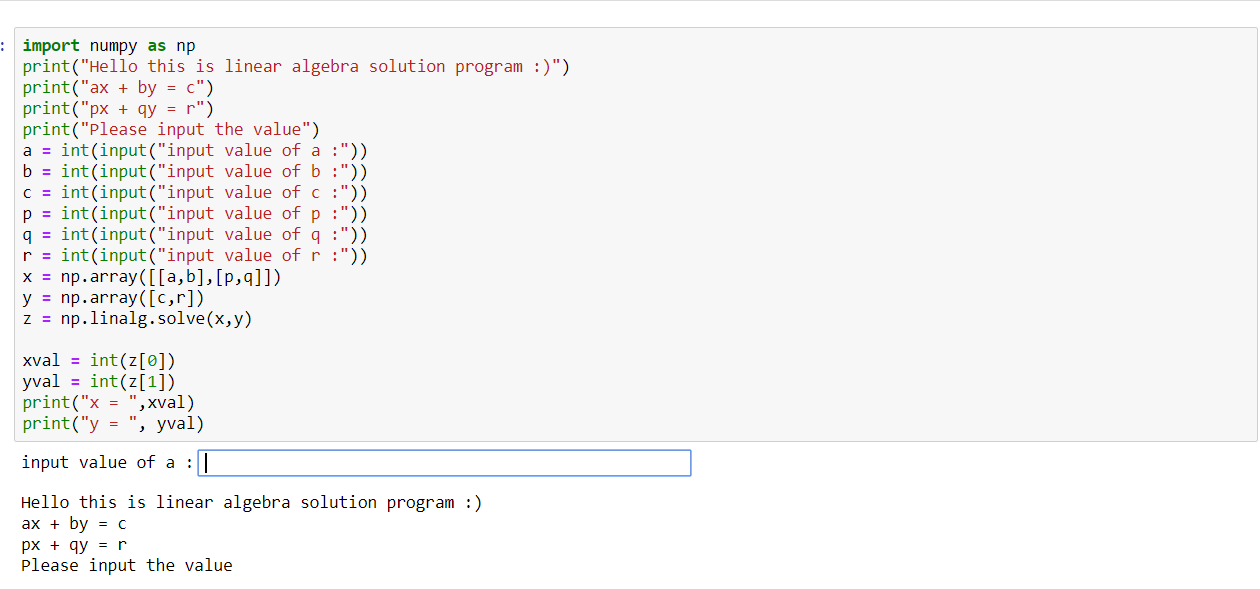
Coding :

import numpy as np

print("Hello this is linear algebra solution program :)")

print("ax + by = c")

print("px + qy = r")

print("Please input the value")

a = int(input("input value of a :"))

b = int(input("input value of b :"))

c = int(input("input value of c :"))

p = int(input("input value of p :"))

q = int(input("input value of q :"))

r = int(input("input value of r :"))

x = np.array([[a,b],[p,q]])

y = np.array([c,r])

z = np.linalg.solve(x,y)

xval = int(z[0])

yval = int(z[1])

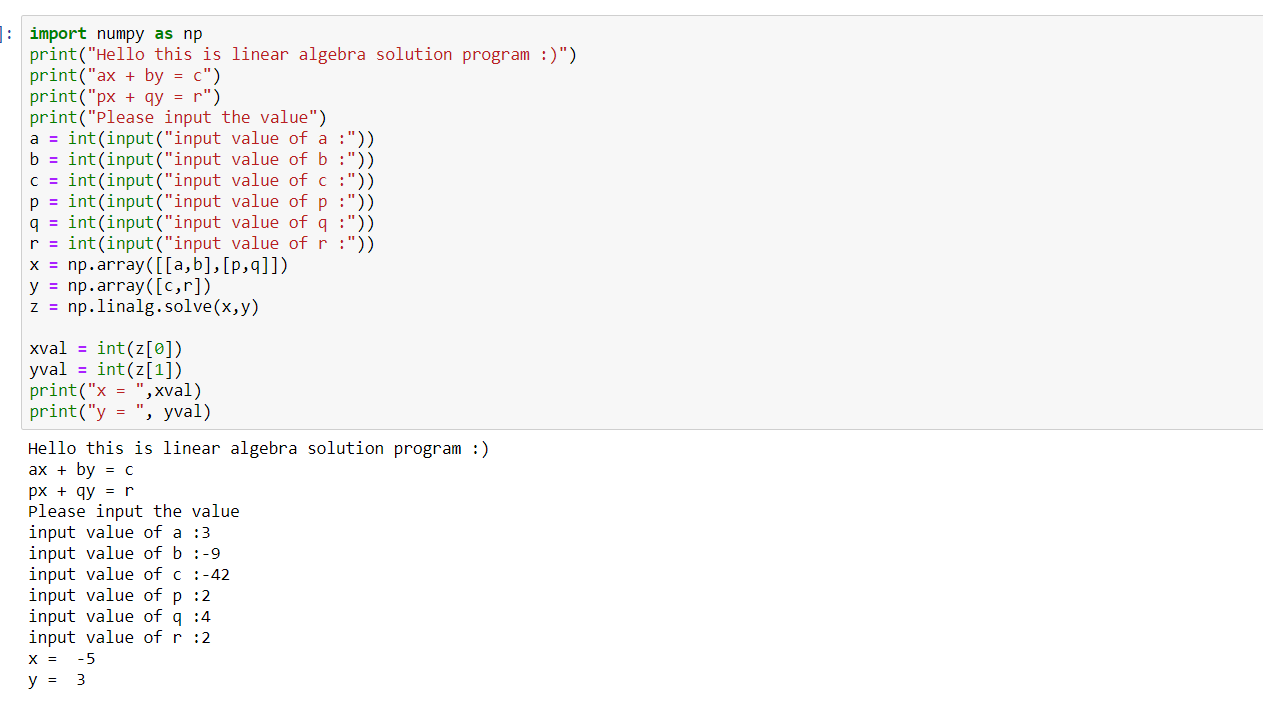
print("x = ",xval)

print("y = ", yval)

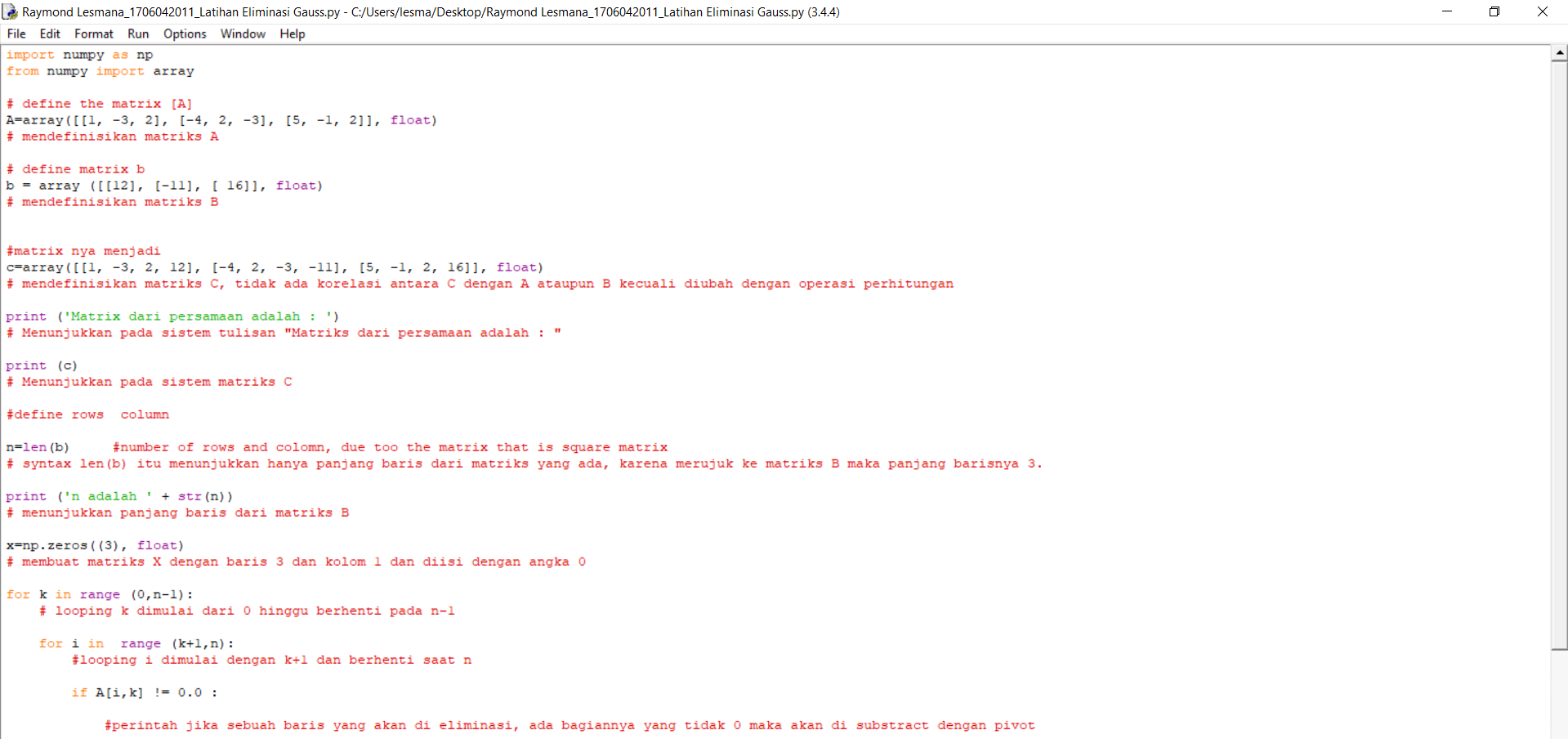
PR Eliminasi Gauss

1. Soal

2. Eliminasi Gauss Jordan halaman 41

[[File:[PRhal40.png]]