Tugas dan Review Pertemuan 5

Pendahuluan

Pada pertemuan kali ini, Bang Edo menjelaskan mengenai optimasi metode numerik pada aplikasi python.

Optimasi adalah suatu proses untuk mencapai hasil yang ideal atau optimasi (nilai efektif yang dapat dicapai). Optimasi dapat diartikan sebagai suatu bentuk mengoptimalkan sesuatu hal yang sudah ada, ataupun merancang dan membuat sesusatu secara optimal. Atau dapat pula disebut dengan membuat sesuatu seoptimal/sebaik mungkin. Suatu persamaan matematis pada dasarnya dapat diselesaikan dengan metode optimasi.

Terdapat cara dalam melakukan optimasi pada python. Berikut merupakan cara meng-optimasi:

1. Menentukan persamaan yang dipakai untuk melakukan optimasi

2. Menentukan alokasi yang efekif dalam memilih sumber yang tersedia

3. Mendesain dengan karakteristik se-optimal mungkin

4. Optimasi membutuhkan batasan untuk bekerja dengan baik, maka dari itu diperlukan algoritma optimasi

5. Melakukan pengecekan pada variable yang dipakai agar sistem bekerja dengan sesuai yang diinginkan/optimal

Optimasi dapat dilakukan melalui aplikasi metode numerik seperti python dengan bantuan Library Scipy.

Algoritma yang dipakai

Berikut merupakan algoritma optimasi yang diajarkan oleh Bang Edo yang nantinya dipakai untuk menghitung optimasi pada tugas yang diberikan:

""" Created on Fri Mar 13 17:11:27 2020

@author: Fadillah Nurrani """

import numpy as np from scipy.optimize import minimize

#python m pip install scipy

def objective (x):

   x1 = x[0] 
   x2 = x[1]
   x3 = x[2] 
   x4 = x[3] 
   return (x1*x4*(x1+x2+x3)+x3) 

def constraint (x):

   return (x[0]*x[1]*x[2]*x[3]-25.0)
#(x1*x2*x3*x4-25>= 0) 

def constraint2 (x):

   sum_sq = 40 
   for i in range (4): 
       sum_sq = sum_sq - x[i]**2

1. return (40 - x1**2 + x2**2 + x3**2 + x4**2)

   return sum_sq

x0 = [1,5,5,1] print(objective(x0))

b= (1.0,5.0) bnds = (b,b,b,b) con1 = {'type' : 'ineq' , 'fun':constraint} con2 = {'type' : 'eq' , 'fun':constraint2} cons = [con1, con2]

sol = minimize (objective, x0, method = 'SLSQP', bounds = bnds, constraints = cons) print (sol)

Yang kemudian didapatkan hasil sebagai berikut:

    fun: 17.01401724563517
    jac: array([14.57227015,  1.37940764,  2.37940764,  9.56415057])
message: 'Optimization terminated successfully.'
   nfev: 30
    nit: 5
   njev: 5
 status: 0
success: True
      x: array([1.        , 4.7429961 , 3.82115462, 1.37940765])

Tugas

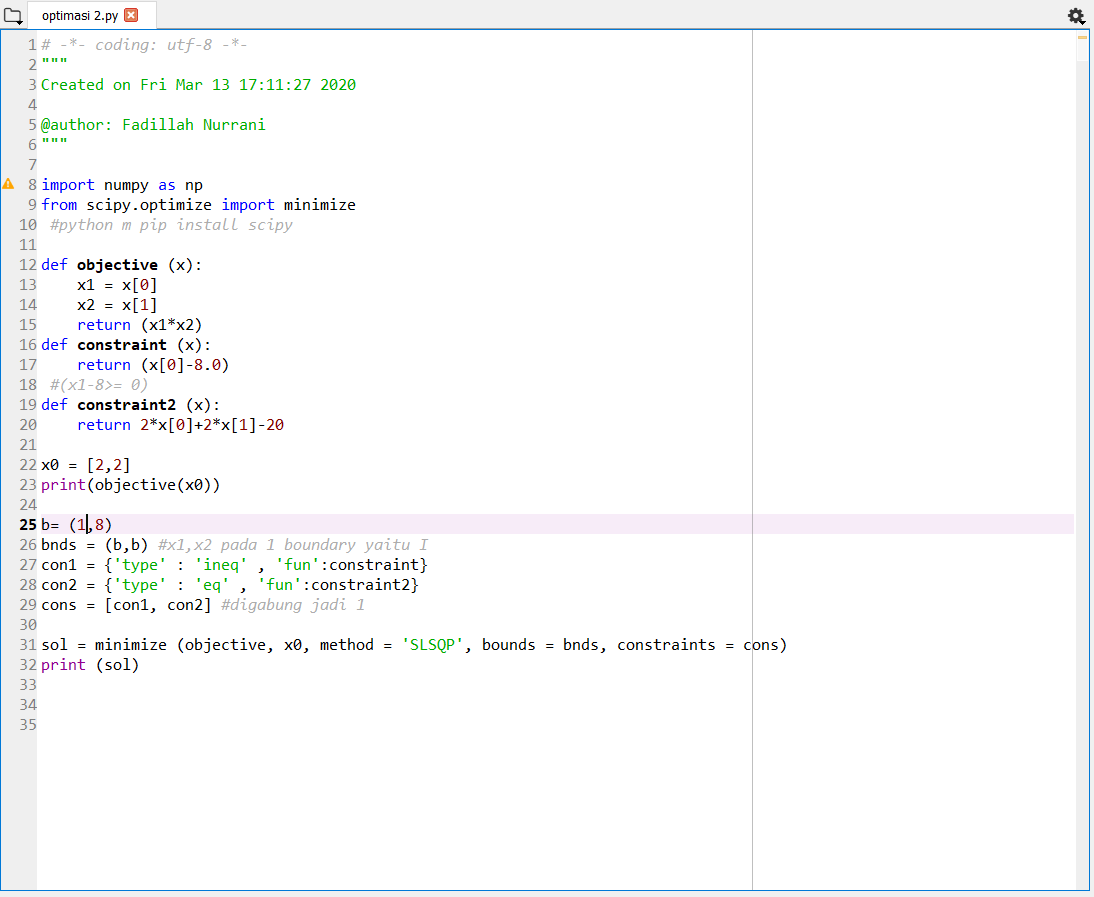
Bang Edo memberikan sebuah kasus dimana menghitung kayu sepanjang 20 meter untuk dipakai pada pagar rumah.

SOAL: Kayu sepanjang 20 meter dibutuhkan untuk membuat pagar rumah. Terdapat permintaan dimana di dalamp pagar harus ada minimal panjang kayu yaiu 8 meter yang dibutuhkan untuk bermain bola. Bagaimana agar kayu tersebut dapat memagari rumah dengan luas yang paling besar/optimal.

Tugas ini dikerjakan dengan fungsi objektif.

Fungsi objektif pada kasus ini adalah:

-Luas halaman (A= P x L)

Permasalahan:

Dalam mengerjakan proses optimasi pada python dibutuhkan yang namanya CONSTRAINT/batas/limit. Fungsi Cons adalah untuk membatasi nilai sehingga tidak keluar dari nilai yang diinginkan.

CONSTRAINT pada kasus ini adalah:

20 meter kayu, sehingga 2P + 2L = 20 (2 karena panjang dan lebarnya ada 2).

Panjang minimal 8 meter sehingga terdapat cons lagi yaitu CONSTRAINT = 2

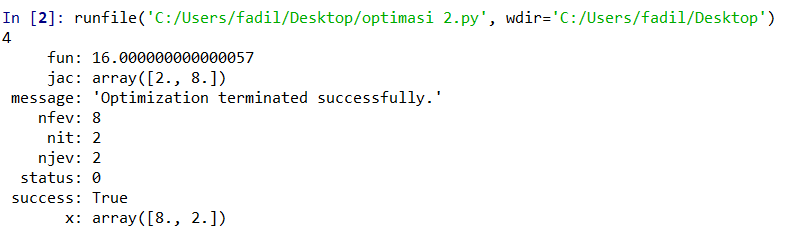
Hasil Pengerjaan

Menggunakan algoritma yang telah dikerjakan didapatkan hasil sebagai berikut:

Sehigga hasilnya terbukti benar:

Kesimpulan

Optimasi dapat berguna dalam kehidupan sehari-hari. Semua yang berhubungan dengan persamaan matematis dapat diselesaikan dengan menggunakan metode numerik. Jika bukan karena ilmu yang diberikan oleh Allah SWT, maka ilmu yang disampaikan tidak akan berguna jika tidak diiringi dengan kerja keras dan belajar lagi :).