Yose Satyanegara

Mahasiswa UI

BIODATA

Nama Lengkap  : Yose Satyanegara NPM  : 1806202525 Tempat, tanggal lahir  : Jakarta, 23 September 1998 Tempat tinggal saat ini : Asrama Narangan, Kober, Depok, Jawa Barat. Domisili  : Kota Batam, Kepulauan Riau. Hobi  : Melukis, Mendesain, dan mendengarkan musik.

BIOGRAFI

Yose Satyanegara merupakan seorang mahasiswa yang sedang mengambil studi di fakultas teknik, program studi teknik perkapalan, Universitas Indonesia. Dia merupakan mahasiswa aktif dari tahun 2018 hingga sekarang. Dia memiliki ketertarikan dalam bidang seni dan artistik, sehingga hobinya adalah menggambar, mendengarkan music dan mendesain grafis. Yose sendiri merupakan mahasiswa berdomisili Kota Batam, Kepulauan Riau.

TUGAS - 1

PERHITUNGAN MANUAL Deskripsi: Pada awalnya, fungsi ini tidak dapat mendefinisikan pada saat x = 1, sehingga saya perlu melalukan perhitungan dengan metode lain yaitu menggunakan limit yang mendekati nilai x = 1. Sehingga hasilnya di dapatkan melalui limit yaitu f(x) = 2.

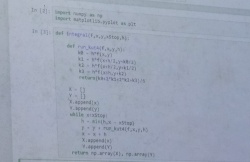
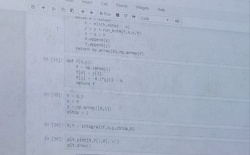
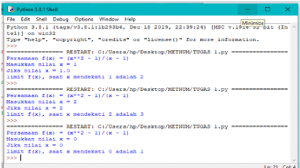PERHITUNGAN MELALUI PROGRAM PYHTON

Prosedur 1. Awalnya, saya mempelajari terlebih dahulu cara-cara input data pada program Pyhton 2. Kemudian saya membuka aplikasi idle.pyhton 3. lalu, saya membuka page baru 4. Saya input data saya sesuai kode input sesuai penggunaannya pada penginputan data 5. Saya masukan data-data yang saya ingin dapatkan sesuai Perhitungan manual 6. Setelah semua data saya input dan hasil didapatkan, saya "run module" pada tab "run" 7. Data-data saya akan otomatis terinput kembali di main page phyton.

PERTEMUAN KE-2 (14/2/2020)

PEMBAHASAN: Di kelas Metode Numerik oleh Pak DAI, kami diajarkan prinsip melawan KEM (Ketidakmauan, Egois, Malas). Kita juga diajarkan tahap-tahan pembelajaran yaitu memperoleh data --> mendapatkan Informasi --> mengambil pengetahuan --> mendapat ilmu yang bermanfaat --> mendapat hikmah --> kemudian menghasilkan hidayah

selain tahap tersebut, terdapat tahap secara teoritis yaitu ketika kita memperoleh data --> lalu kita analisis yang dibagi 2 secara garis besar yaitu Statistika dan Deterministik

Statistika --> Data Diskrit (pengukuran aktual) --> Stokastik

Deterministik --> Contohnya persamaan differensial (Hk. Fisika)

- Kenapa 0/0 sama dengan tak terdefinisi?

Karena berdasarkan penyebut, bilangan apapun yang dibagi 0 itu sama dengan tak terdefinisi.

- Materi Bab 2: Aljabar Linear

Berdasarkan materi yang sekilas saya baca, saya menemukan materi aljabar linear dengan a.) Metode eliminasi Gauss b.) Metode Dekomposisi LU c.) Metode eliminasi Gauss-Jordan yang cukub membuat saya tertarik untuk dipelajari. Mengapa? karena materi-materi tersebut merupakan materi yang baru saja saya pelajari di semester lalu. Saya tertarik untuk eksplor lebih dalam terkait materi ini baik pendalamannya dan aplikasinya dalam program.

Kaidah program pyhton untuk metode eliminasi Gauss-Jordan

(source: Buku Numerical Methods In Engineering with Python 3)

TUGAS - 2

'''PENGERJAAN SOAL BAB 2 - METODE GAUS'''

MANUAL

Pada soal ini diketahui matrik A dan matriks B, kemudia ditanyakan matriks X dari persamaan A.X=B sehingga kita harus melakukan eliminasi Gaus dengan menggabungkan matriks kemudian melakukan eliminasi sehingga ruas segitiga bawa bernilai 0 yang artinya pada baris ketiga hanya terdapat 1 variable kemudian baris kedua hanya 2 variable dan ketiga tiga variable. Sehingga kita mendapatkan nilai variable X31 kemudian disubtitusi dengan X21 dan selanjutnya X11 dihasilkan matriks untuk X1 Pada X2 kita juga melakukan hal yang sama yang kemudian kita mendapatkan matriks X2.

PROGRAMMING CODE

Pada programming, saya menggunakan Anaconda Python kemudian saya mengerjakan soal tersebut dengan coding numpy saya memasukan data-data yang ada kemudian memasukan code-code yang berlaku pada program untuk mendapatkan hasil. Dapat disimpulkan menggunakan programming jauh lebih mudah dan efektif untuk mendapatkan hasil pada perhitungan matriks ini.

'''INITIAL VALUE'''

MANUAL

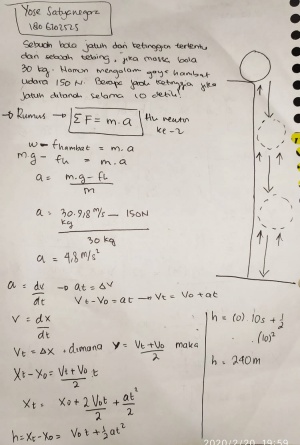
Pada solusi manual, saya menggunakan rumus pokok F = m.a yang merupakan hukum kedua newton dengan mempertimbangkan gaya yang bekerja pada bola adalah gaya beratnya yang membawanya turun kebawah dan gaya hambat udara yang merupakan pengaruh gerak angin terhadap bola. Asumsi penyelesaian adalah positif untuk semua arah yang mengarah ke bawah(sesuai dengan gerak jatuh penerjun). Kemudian setelah didapat percepatan yang dialami oleh bola, saya menghitung ketinggian yang ditanya terhadap waktu yang telah ditentukan untuk mencapai tanah. Rumus ketinggian h = V0t + at²/2 merupakan bagian dari fungsi jarak terhadap waktu xt = x0 + V0t + at²/2 yang merupakan turunan dari fungsi kecepatan v = dx/dt. Maka saya menyimpulkan soal ini merupakan tipe soal initial value problem. Berikut penyelesaian secara manualnya :

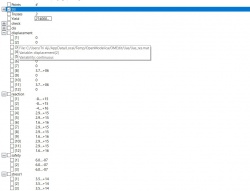
PROGRAMMING CODE Pada solusi dengan aplikasi Spyder(Python3.7) saya menginput data-data yang diketahui di soal, kemudian membuat rumusnya, dan mendapatkan percepatan yang dicari. Setelah percepatan didapat, saya menghitung ketinggian yang dicari dengan menginput rumus juga h = V0t + at²/2 dengan kode h = v0*t + (a*t**2)/2 dan kemudian memasukkan kode print("maka ketinggian yang dialami bola bebas setinggi", h,"m"). Lalu didapat ketinggian bola hingga sampai ke tanah. Berikut penyelesaiannya :

PROGRESS PEMBELAJARAN

Berikut merupakan progress pembelajaran yang telah saya dapatkan selama 3 pertemuan terakhir di kelas metode numerik bersama pak Dai.

PERTEMUAN KE-3 (21/02/2020)

PEMODELAN

Apa itu frekuensi? --> Frekuensi merupakan gerak naik turun dalam kurun waktu. Suara memiliki frekuensi yang terdapat gelombang. Selain itu juga pegas masa juga memiliki frekuensi gelombang yang terjadinya gerak osilasi.

TUGAS - 3

Pada tugas kali ini saya mengaplikasikan metode runge kutta pada contoh soal. Berikut Contoh Soalnya:

Saya menggunakan aplikasi spyder Anaconda python untuk menjawabnya:

LAPORAN ASISTENSI (25/02/2020)

Pada hari itu, kami mendapat asistensi dari senior kami bernama Michael Ahli. Dia mengajar kami berbagai materi seperti metode runge kutta serta pengaplikasiannya dalam program koding python. Berikut merupakan beberapa yang sudah diajarkan:

PERTEMUAN KE-4 (28/02/2020)

Pada pertemuan kali ini, kami diajarkan mengenai Boundary Value Problem dimana kita diajarkan menggunakan aplikasi CFD yang menggunakan aplikasi contoh kasus aliran air pada sebuah kapal. Pengaplikasiannya dengan model matematik.

Kita juga belajar mendefinisikan apa itu model matematik? Dari hasil diskusi bersama, kita mendapatkan pengertian model matematik merupakan suatu contoh acuan yang merepresentatifkan solusi terbaik dari suatu problem. Kemudian kita mendapatkan 1 set persamaan aljabar baik itu dari metode jacob, gauss, NF, dll dari nilai numerik.

Kita dituntut untuk mendapatkan hambatan dari sebuah pengaplikasian model matematik ini dengan meregresinya melalui aplikasi CFD. Kita diajarkan tutorial penggunaan CFD oleh asistensi senior kami. Kemudian karena waktu terbatas, sehingga asistensi kami akan memberikan video tutorial untuk dipelajari di rumah. Kemudian kami dituntut untuk mendapatkan 10 variasi hambatan dari kecepatan yang kita tentukan sendiri. Di hari selasa, kita akan melakukan asistensi untuk melanjutkan materi setelah mendapatkan data hambatan dari kecepatan.

LAPORAN ASISTENSI (3/03/2020)

Sebelumnya kami mendapat tugas terkait mencari hambatan dari 10 masing-masing kecepatan menggunakan aplikasi CFD.

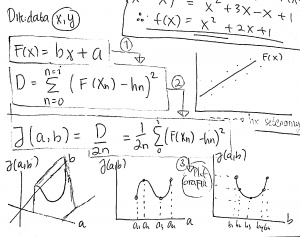
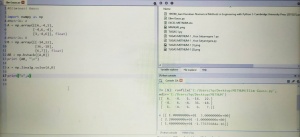
Pada pertemuan ini kami akan mendapat pembekalan materi terkait regresi menggunakan koding python dan pengerjaan manual. Dari hasil data yang kita temukan kita inisialkan x = kecepatan initial dan y = hambatannya. Sigma (x,y) = (11, 609);(10,502);(9,407);(8,321);(7,246);(6,180);(5,125);(4,80);(3,45);(2,91 Hasil data ini kemudian kita masukkan fungsi kodingnya untuk mendapatkan persamaan fungsinya.

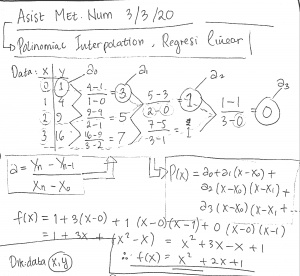
Jika ingin memastikan hasil dari koding, kita dapat menggunakan cara menghitung langsung dengan melakukan polinomial interpolasi.