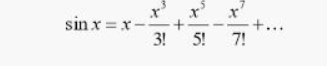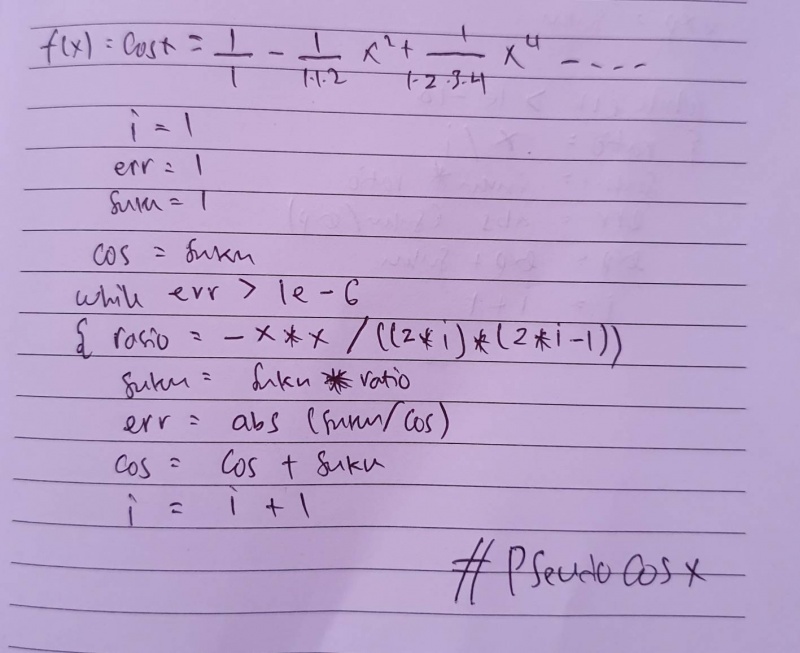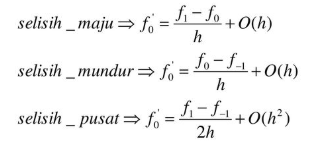Yoshua Lian Calvin
| Profile | |
|---|---|

| |
| Nama Lengkap | Yoshua Lian Calvin |
| NPM | 1706036476 |
| Jurusan | Teknik Mesin/ Reguler |
Contents
PERTEMUAN 1
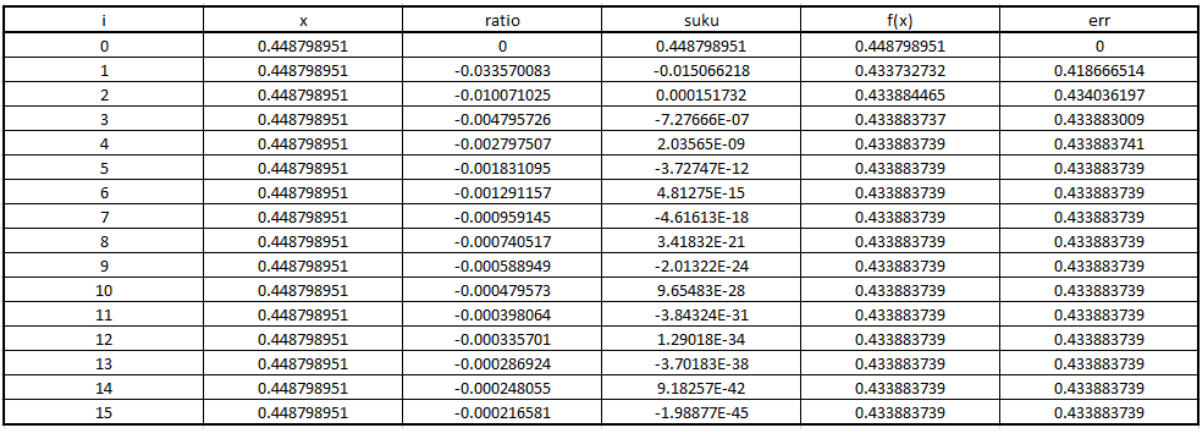
Metode Numerik adalah operasi memformulasikan persamaan matematika. Karena batasan kemampuan penghitungan manusia dan kalkulator sederhana maka penghitungan numerik menggunakan komputasi. Salah satu komputasi paling sederhana menggunakan Microsoft Excel. Dengan komputasi dapat melakukan penghitungan dengan efisien dan akurat. Pada materi kelas ini formulasi yang digunakan yaitu menghitung deret taylor dari sin (phi/7). Deret Taylor ini untuk mengakpromisasikan nilai fungsi dengan jumlah dari turunan yang tak berhingga, dalam kasus ini dicari nilai sin (phi/7). Dalam menghitung fungsi ini terdapat beberapa konstanta yaitu : i = turunan ke-i
x = phi/7
Ratio = suku n / suku n-1 yang dimasukan dengan rumus =-1*(Nilai X)²/((2*Nilai i)*(2*Nilai i + 1))
Suku = Dimasukan dengan rumus = Suku ke n*Rasio pada nilai i
Fungsi = Dimasukan dengan rumus =Fungsi ke n-1 + Suku ke n
Error = Dimasukan dengan rumus =ABS(suku ke n/fumgsi ke n-1
PERTEMUAN 2
Hari, Tanggal : Selasa, 10 September 2019
Pengajar : Dr. Ir. Engkos Achmad Kosasih M.T.
Pada pertemuan ke-2 Kelas Metnum, Pak Engkos mengajarkan tentang bahasa pemograman. Bahasa pemograman sendiri itu adalah media instruksi komputer untuk menjalankan perintah yang diberikan. Bahasa pemograman paling rendah yaitu binary yang hanya terdiri dari 0 dan 1. Namun untuk menerjemahkan bahasa manusia ke bahasa binary dibutuhkan mesin penerjemah yang disebut complier. Pseudocode sendiri berarti kode imitasi karena tidak dapat diterjemahkan complier namun pseudocode ini menggunakan bahasa manusia sehingga dapat dimengerti langsung. Pseudocode memberikan garis besar instruksi dan dimana dapat menjadi acuan untuk membuat bahasa pemogramannya.
PERTEMUAN 3(17 Sept 2019)
Oleh : Dr. Ir. Engkos Achmad Kosasih M.T.
Pada kelas Metode Numerik Pertemuan ketiga ini, Kita diajari tentang turunan numerik. terdapat 3 pendekatan dalam turunan numerik seperti yang dibawah ini :
Jika nilai h sama, turunan pusat adalah metode yang paling akurat.
Kemudian, pada hari itu juga setelah kami diajarkan Turunan Numerik, materi kelas dilanjutkan oleh Asisten Kelas, yaitu Bang Hanif Furqon Hidayat. kami diperkenalkan dengan bahasa pemrograman C++. C++ itu sendiri merupakan bahasa pemrograman yang berorientasi pada Objek. Kami Diajarkan untuk memindahkan Pseudocode Pada pertemuan Kedua kedalam C++.
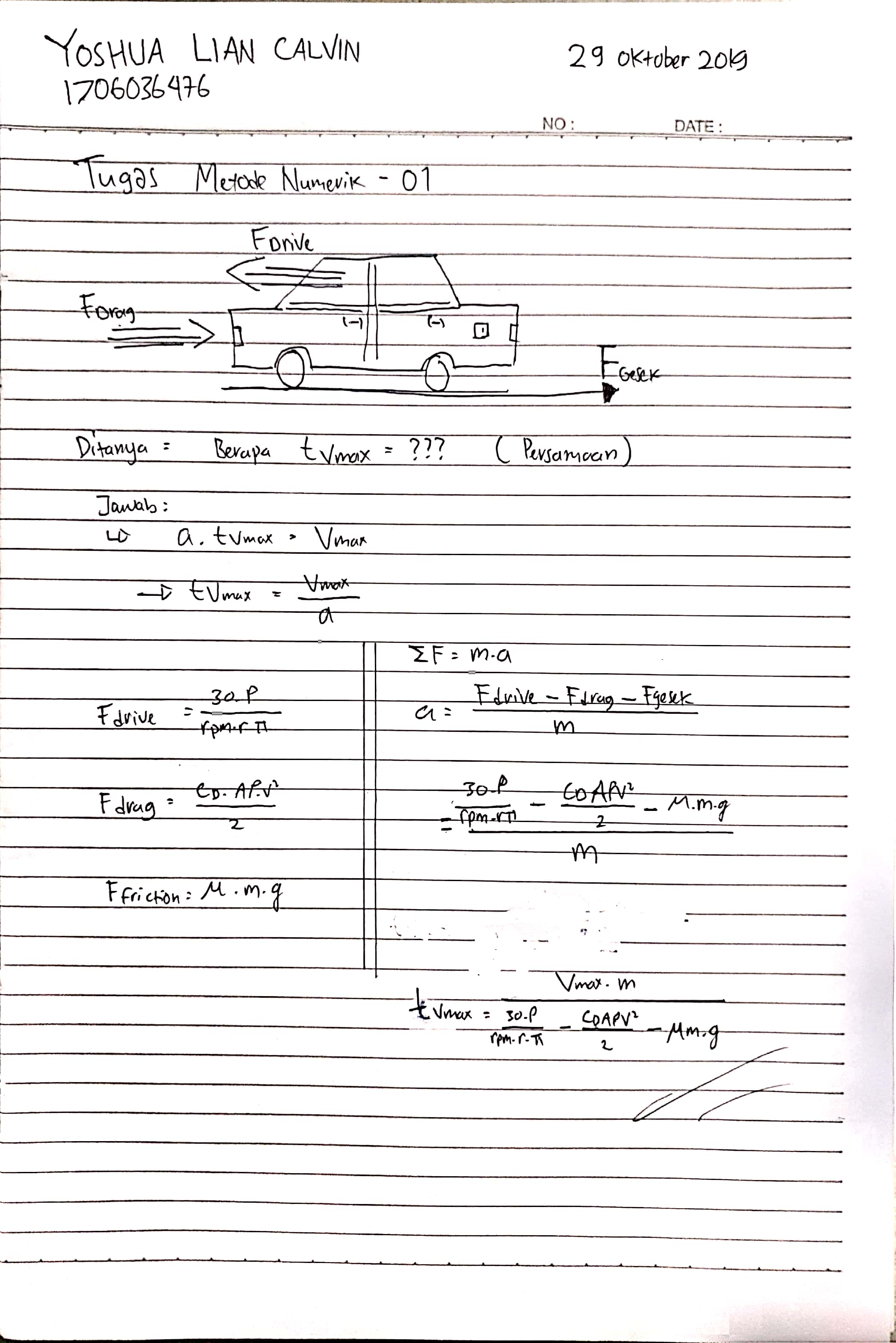
Tugas Metode Numerik, 29 OKTOBER 2019
Pertemuan hari ini yang diajarkan oleh Bapak Dr. Ir. Ahmad Indra Siswantara membahas Python secara pemula, disertai beberapa command sederhana. Dalam pertemuan ini, juga diberikan soal latihan dalam bentuk narasi. Kelas diinstruksikan untuk mencari waktu yang diperlukan oleh suatu mobil, dengan ketentuan bhp, torsi, dll ditentukan kelompok, untuk mencapai kecepatan maksimal, dari posisi diam. Terdapat juga tugas yang diberikan oleh Pak Dai pada saat tadi pagi kelas yaitu seperti :
>>> 3+4
7
>>> import math
>>> math.sqrt (99)
9.9498743710662
>>> akardari = math.sqrt
>>> akardari (9)
3.0
>>> x=30
>>> y=20
>>> z=10
>>> x+y+z
6.0
>>> x-y-z
0
>>> pow (x,y)
34867844010000000000000000000
>>> string1 = 'internal transmision'
>>> string2 = 'three speed shimano'
>>> print (string + + string2)
Traceback (most recent call last) :
File "<pyshell#", line 1, in <module>
print (string + + string2)
internal transmision 3 speed shimano
>>> print (string1[0:11])
intrnal tr
>>>
Jawaban dari tugas yang diberikan oleh Bapak Dai pada kelas pagi hari ini :
PERTEMUAN 5 November 2019
Metode Numerik dapat dilakukan dalam metode brainware, software dan hardware. Dalam menyelesaikan masalah brainware, dibutuhkan permasalahannya yaitu Engineering Problem (Real Life Case). Contoh-contoh dari Engineering Problem adalah Initial value problem dalam kasus soal adalah top speed problem dan Boundary value problem dalam kasus ini adalah aerodynamics. Untuk menyelesaikan permasalahan engineering yang ada adalah dengan menentukan model. Model bisa dalam bentuk math atau physical. Setelah menentukan model, kita harus mempelajari kasus dan modelnya sehingga menemuka solusi dari permasalahan yang berupa Analysis Results yang sudah valid/accepted. Namun dalam menyelesaikan masalah kita bisa menggunakan software yang ada lalu bisa langsung menemukan solusinya. Software yang bisa digunakan adalah CFD, FEA, AI (Neural Network) dan Optimization.
Runge Kutta Method
Persamaan Diferensial Biasa (PDB) adalah persamaan yang melibatkan satu atau lebih turunan fungsi satu peubah. Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi, dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f(x, y) pada titik terpilih dalam setiap selang langkah.

PERTEMUAN 12 NOVEMBER 2019
Kuliah Metode Numerik, 12 November 2019
Pada pertemuan 12 November 2019 mahasiswa mempelajari Metode Runge-Kutta. Metode ini adalah metode yang termasuk dalam golongan metode iteratif implisit dan eksplisit, sama seperti dengan metode Euler
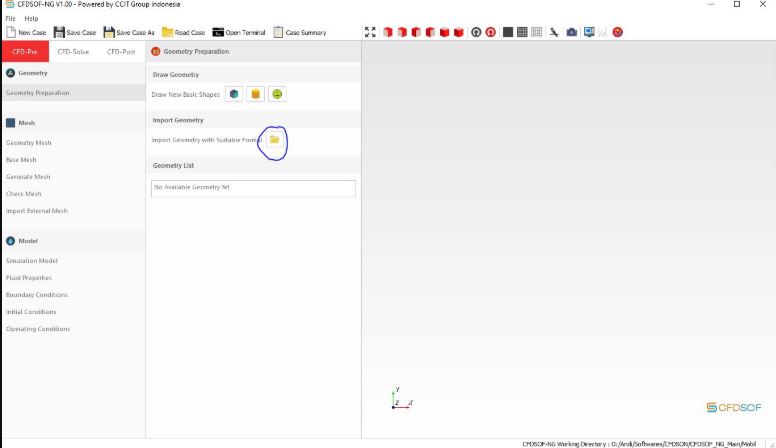
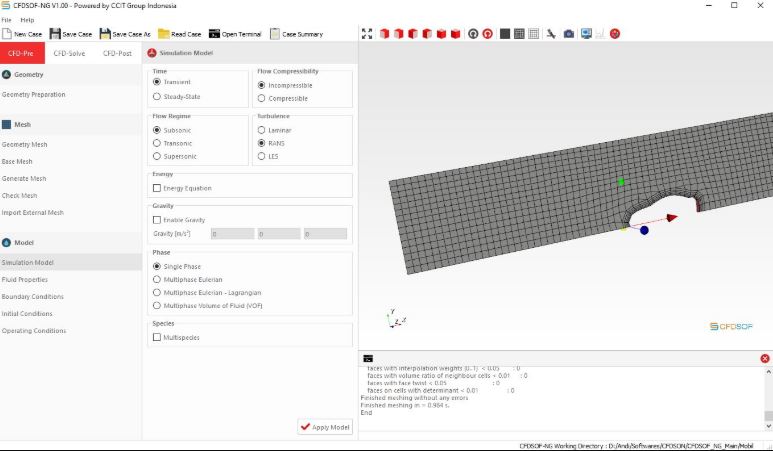
Lalu, mahasiswa mempelajari perangkat lunak CFDSOF-NG. Untuk mempelajari aliran fluida. Langkah yang diajarkan menggunakan CFDSOF adalah sebagai berikut: 1. Buat case baru dengan memasukkan nama proyek, lalu tekan create case
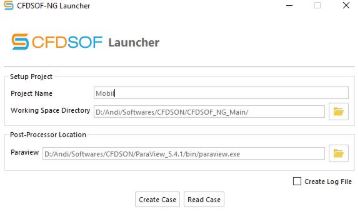
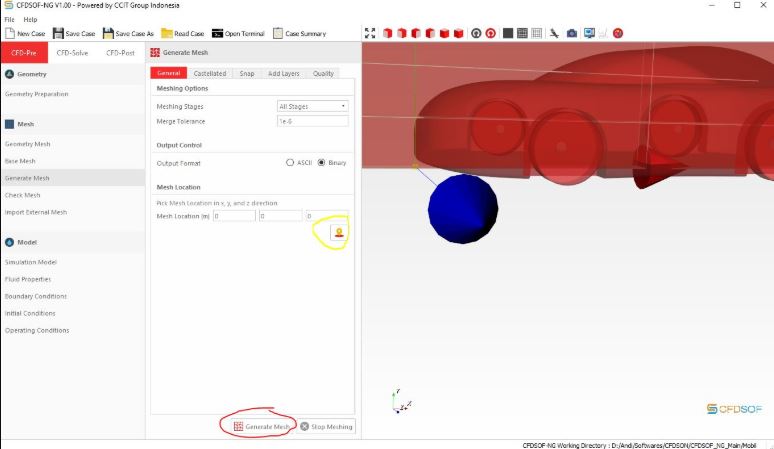
3. Pindah ke bagian base mesh dan ubah mesh sesuai kehendak.
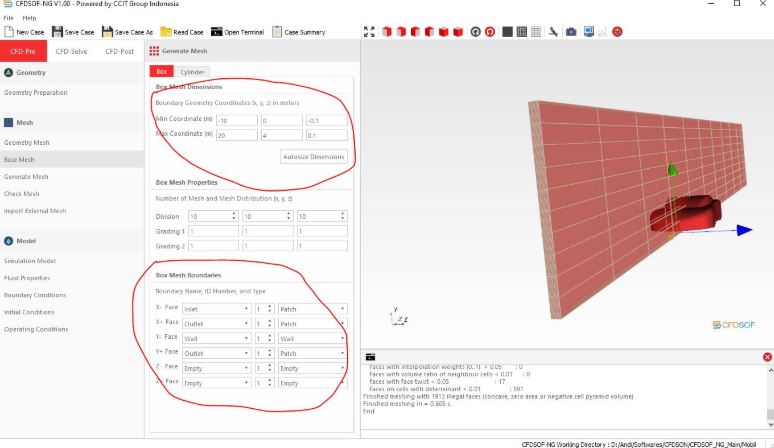
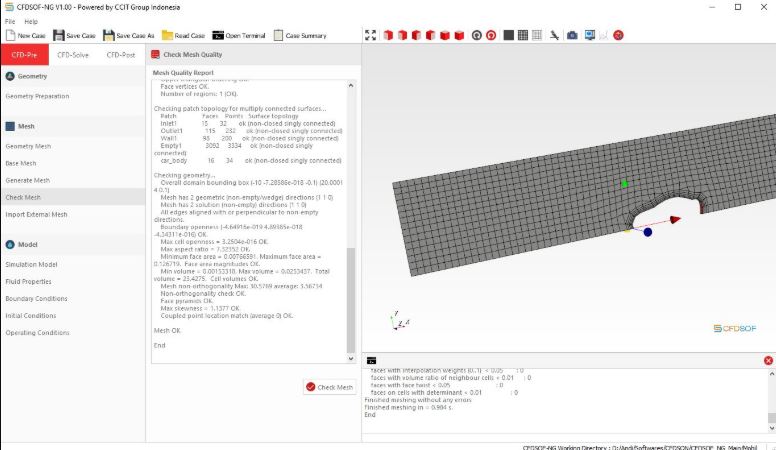
5. Pindah ke bagian check mesh lalu klik check mesh. Jika muncul tulisan mesh OK maka ia siap dipakai
6. Pindah ke bagian Simulation model dan atur kondisi simulasi sesuai keinginan
7. Lalu pindah ke CFD Solve
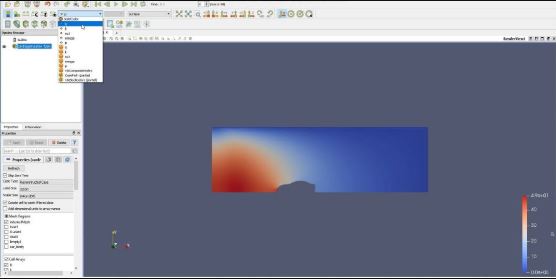
8. Pindah ke CFD-Post untuk melihat hasil simulasi. Setelah itu pindah ke Paraview
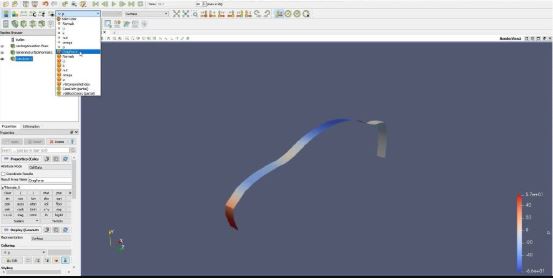
9. Kemudian cari Drag Force
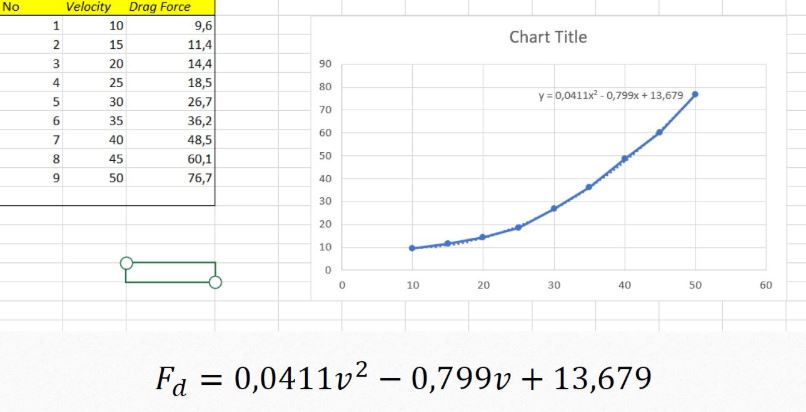
10. Hasil dapat dilihat di bawah: