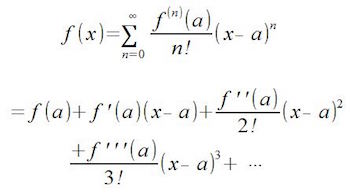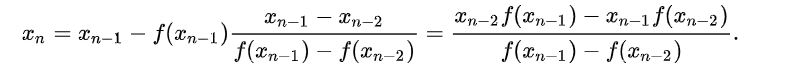Sarah Mahira Adrian
بِسْمِ اللهِ الرَّحْمٰنِ الرَّحيمِ
assalamualaikum warahmatullahi wabarakatuh
| Profile | |
|---|---|

| |
| Nama Lengkap | Sarah Mahira Adrian |
| NPM | 1706986492 |
| Jurusan | Teknik Mesin |
Contents
Pertemuan Pertama
Hari, Tanggal : Selasa, 3 September 2019
Pengajar : Dr. Ir. Engkos Achmad Kosasih M.T. dan Dr. Ir. Ahmad Indra Siswantara
Pada pertemuan pertama kelas Metode Numerik ini, kami diajarkan tentang pengertian metode numerik dan contoh pengaplikasiannya. Metode numerik sangat dibutuhkan oleh seorang engineer karena dalam praktiknya sering sekali ditemukan berbagai data yang sangat kompleks dimana tidak cukup apabila hanyak memanfaatkan kalkulator. Contoh aplikasi dari metode numerik yang dijelaskan oleh Pak Engkos adalah pengolahan data menggunakan microsoft excel dengan menggunakan Deret Taylor.
Rumus dari Deret Taylor tersebut adalah sebagai berikut:
Apabila deret tersebut terpusat di titik nol, deret tersebut dinamakan sebagai Deret Maclaurin
Pada pertemuan pertama ini, kami diberikan tugas untuk mencari nilai dari Sin(π/7) menggunakan Deret Taylor tersebut di microsoft excel.
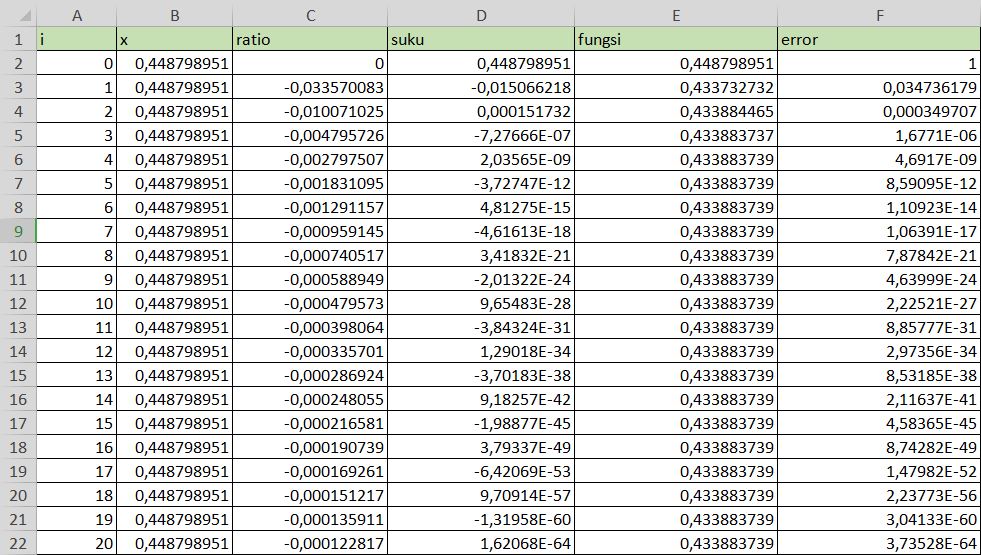
Berikut hasilnya:
Diperoleh bahwa hasil dari Sin(π/7) adalah 0,433883739
Keterangan:
1. Nilai x adalah π/7
2. Untuk mencari Rasio pada kotak C3 dapat menggunakan rumus =-1*B2^2/(2*A3)/(2*A3+1)
3. Untuk mencari Suku pada kotak D3 dapat menggunakan rumus = D2*C3 atau disebut juga dengan mengalikan suku sebelumnya dengan rationya
4. Untuk mencari Fungsi pada kotak E3 dapat menggunakan rumus = E2+D3 atau disebut juga dengan menjumlahkan fungsi sebelumnya dengan suku sekarang
5. Untuk mencari Error pada kotak F3 dapat menggunakan rumus = ABS(D3/E3) atau disebut juga dengan mencari nilai absolut dari hasil pembagian suku dengan fungsi
Pertemuan Kedua
Hari, Tanggal : Selasa, 10 September 2019
Pengajar : Dr. Ir. Engkos Achmad Kosasih M.T.
Pada pertemuan kedua kelas Metode Numerik, Pak Engkos mengajarkan tentang Pseudocode. Pseudocode merupakan cara penulisan algoritma menggunakan bahasa yang baku agar lebih mudah dipahami oleh manusia. Pseudocode mirip dengan Bahasa Pemrograman namun ditulis lebih sederhana. Tujuan dari penggunaan Pseudocode yaitu untuk memudahkan programer dalam memahami suatu kerangka awal atau ide suatu program dengan jelas dengan cara mendeskripsikan suatu algoritma. Contoh dari penulisan Pseudocode yaitu Basic, pascal, C++ dan lain-lain.
Pada pertemuan ini, kami diberikan latihan soal tentang Pseudocode dimana kita harus menentukan rasio, suku, error, dan nilai i dari fungsi yang sudah diberikan oleh Pak Engkos. Fungsi-fungsi tersebut antara lain adalah sin x, cos x, dan e^x.
Pertemuan Ketiga
Hari, Tanggal : Selasa, 17 September 2019
Pengajar : Dr. Ir. Engkos Achmad Kosasih M.T. dan Bang Hanif Furqon
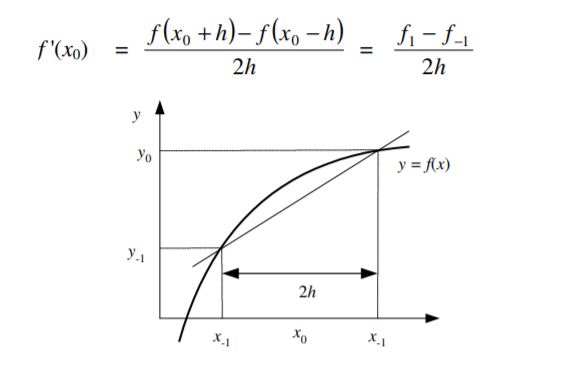
Pada pertemuan ketiga kelas Metode Numerik, kami diajarkan tentang Turunan Numerik. Persoalan turunan numerik ialah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 jenis turunan numerik, yaitu:
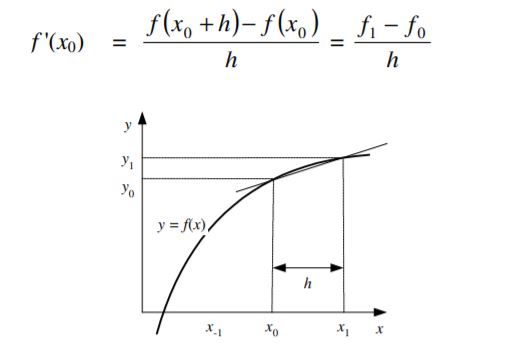
1. Beda maju (forward difference): Hampiran menggunakan informasi di titik xi dan beberapa titik di kanannya, yaitu xi+1, xi+2, ....
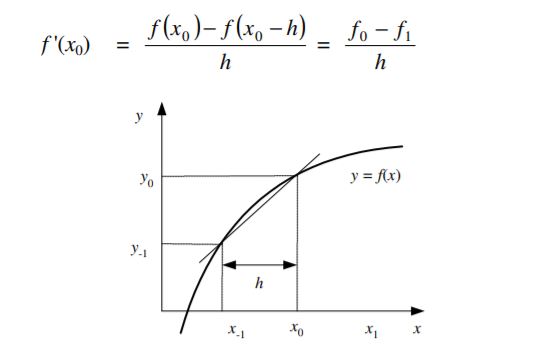
2. Beda mundur (backward difference) : Hampiran menggunakan informasi di titik xi dan beberapa titik di kirinya, yaitu ..., xi−2, xi−1.
3. Beda pusat/tengah (central difference) : Hampiran menggunakan informasi di titik xi dan beberapa titik di kiri dan kanannya secara simetris (sama banyak).
Pertemuan Keempat
Hari/Tanggal : Selasa, 24 September 2019
Pengajar : Dr. Ir. Engkos Achmad Kosasih M.T.
Pada pertemuan ini kami diajarkan tentang Secant Method, Bisect Method, dan Newton Raphson Method.
Bisect Method adalah prosedur numerik yang paling sederhana untuk menemukan akar yaitu dengan berulang kali membagi separuh persediaan [a, b], menjaga separuh dari yang mana f(x) berubah tanda.
Secant Method adalah adalah algoritma pencarian-akar yang menggunakan suksesi akar garis potong untuk memperkirakan lebih baik akar dari suatu fungsi f. Metode garis potong dapat dianggap sebagai pendekatan perbedaan-terbatas dari metode Newton. Rumus dari Secant Method sendiri dapat didefinisikan sebagai
Newton Rhapson Method adalah adalah algoritma pencarian-akar yang menghasilkan perkiraan yang lebih baik berturut-turut ke akar (atau nol) dari fungsi bernilai nyata. Versi paling dasar dimulai dengan fungsi variabel tunggal f yang ditentukan untuk variabel nyata x, turunan fungsi f ′, dan tebakan awal x0 untuk akar f.
Pertemuan Kelima
Hari/Tanggal : Selasa, 1 Oktober 2019
Pengajar : Dr. Ir. Engkos Achmad Kosasih M.T.
Pada pertemuan ini, kami diajarkan tentang Truncation Errors and Validations.
Pertemuan Ke-enam
Hari/Tanggal : Selasa, 29 Oktober 2019
Pengajar : Dr. Ir. Ahmad Indra Siswantara
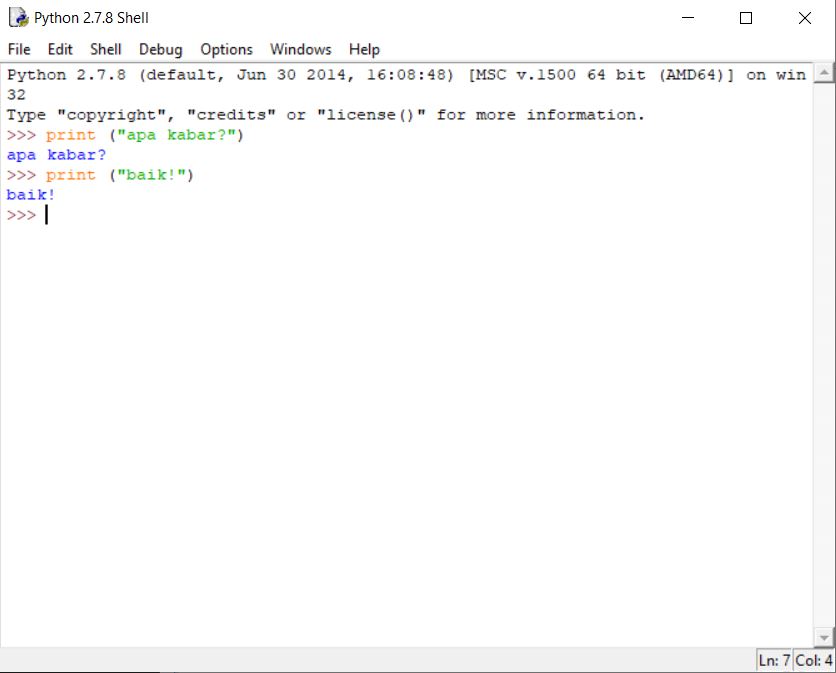
Pada pertemuan ini kami diajarkan tentang cara membuat sebuah Pseudocode mengguakan aplikasi Python.
1. Print
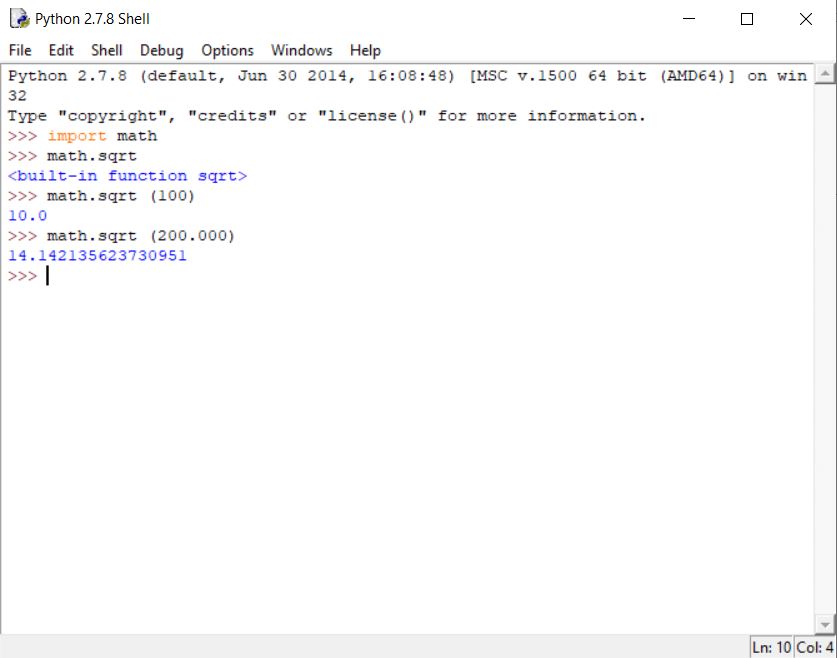
2. Import
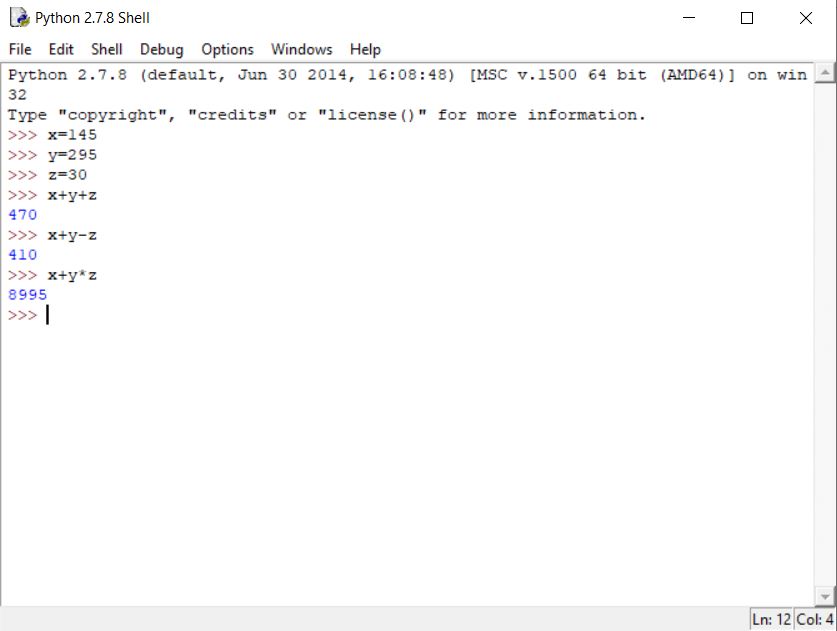
3. Memasukan dan menghitung operasi dari variabel
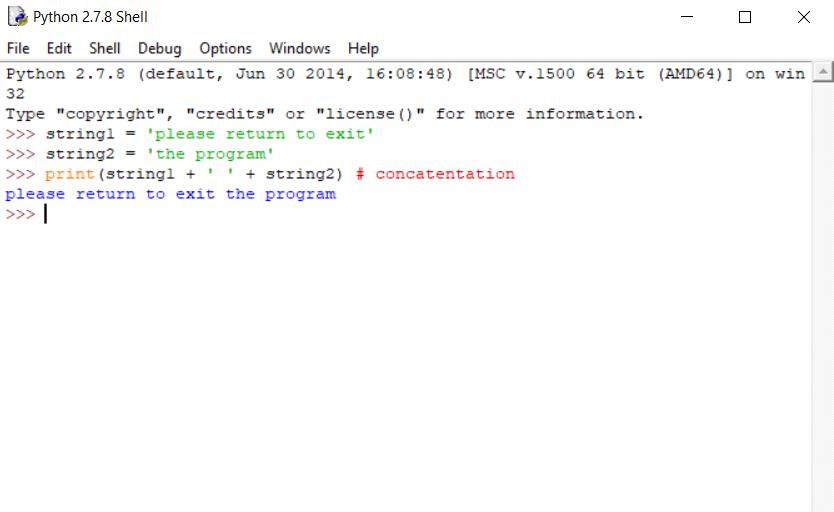
4. String
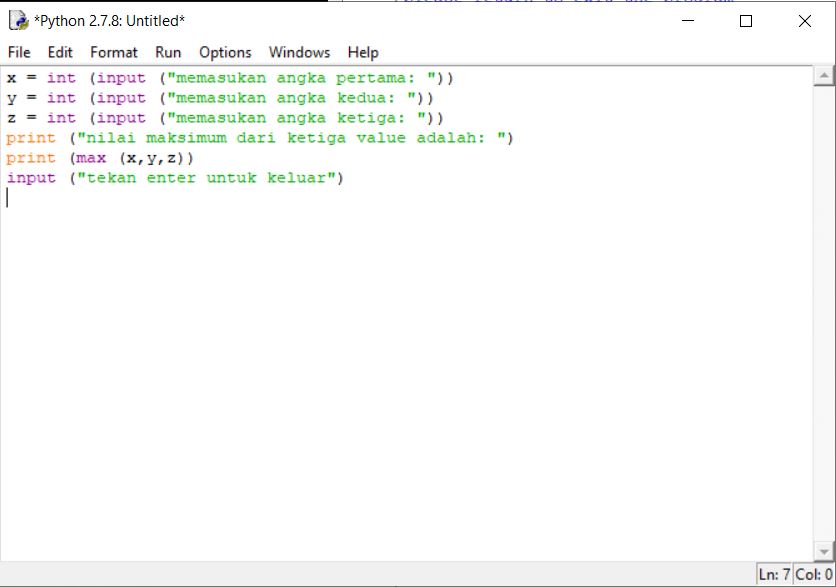
5. Mencari nilai maksimum
Pertama, kita masukan variabel terlebih dahulu
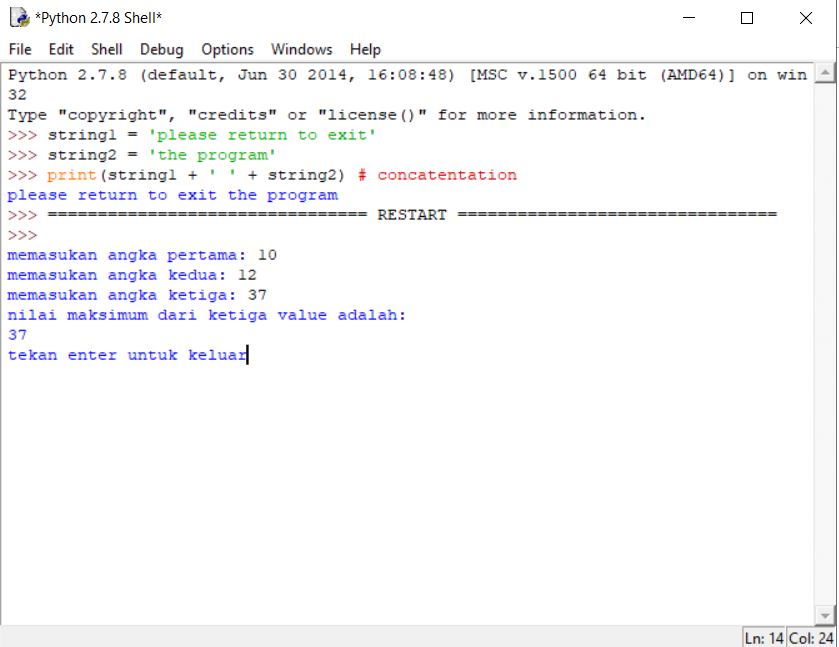
lalu di run
Selain itu kami juga dijelaskan tentang Runge Kutta, dimana merupakan sebuah metode alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan.
Kami diberikan tugas untuk membuat sebuah Governing Equation
Pertemuan ketujuh
Hari/Tanggal : Selasa, 5 November 2019
Pengajar : Dr. Ir. Ahmad Indra Siswantara
Pada pertemuan ini kami dijelaskan tentang Engineering Problem. Contoh-contoh engineering problem dalam kehidupan sehari-hari, yaitu:
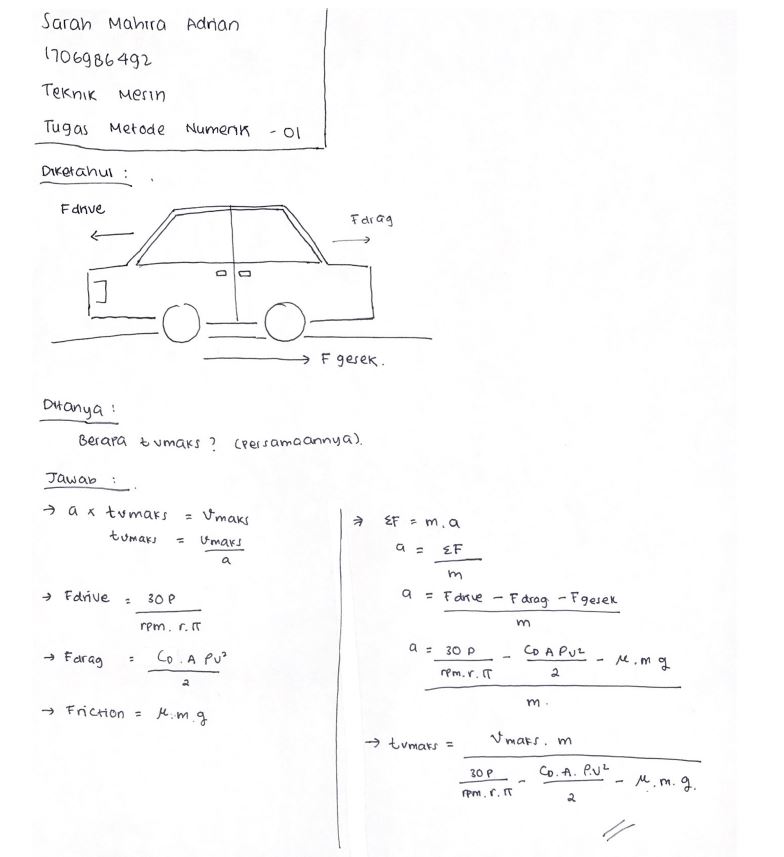
1. Initial Value problem, permasalahan ini biasanya mengenai bagaimana mencari kecepatan maksimum suatu kendaraan
2. Boundary Value Problem, permasalahan ini biasanya mengenai aerodynamics.
Metode numerik terdiri dari 3 komponen yaitu brainware, software, dan hardware. namun komponen utamanya adalah software yang dioperasikan oleh manusia.
Pertemuan Kedelapan
Hari/Tanggal : Selasa, 12 November 2019
Pengajar : Dr. Ir. Ahmad Indra Siswantara
Pada pertemuan ini kami diajarkan tentang Optimasi Aerodinamik. Optimasi merupakan proses untukmencapai hasil yang maksimal.
Kami diberikan tugas untuk kelompok yaitu untuk mencari Optimasi sudut dari sebuah Airfoil dengan Python.
Untuk mencari optimasi sudut dari sebuah airfoil, pertama kami mendesain airfoil terlbih dahulu menggunakan inventor lalu mensimulasikan airfoil tersebut pada CDFSOF-NG dan akan didapat Lift Force dan Drag Force pada setiap sudut yang kami tentukan. Selanjutnya kami memasukan data-data tersebut pada Microsoft Excel dan didapatkan grafik gaya terhadap sudut kemiringan beserta persamaannya. Persamaan yang didapat tersebut selanjutnya akan disimulasikan pada aplikasi python yaitu Jupyter dan dari aplikasi tersebut akan didapatkan hasil optimasinya.
Berikut adalah hasil dari tugas yang kami buat:
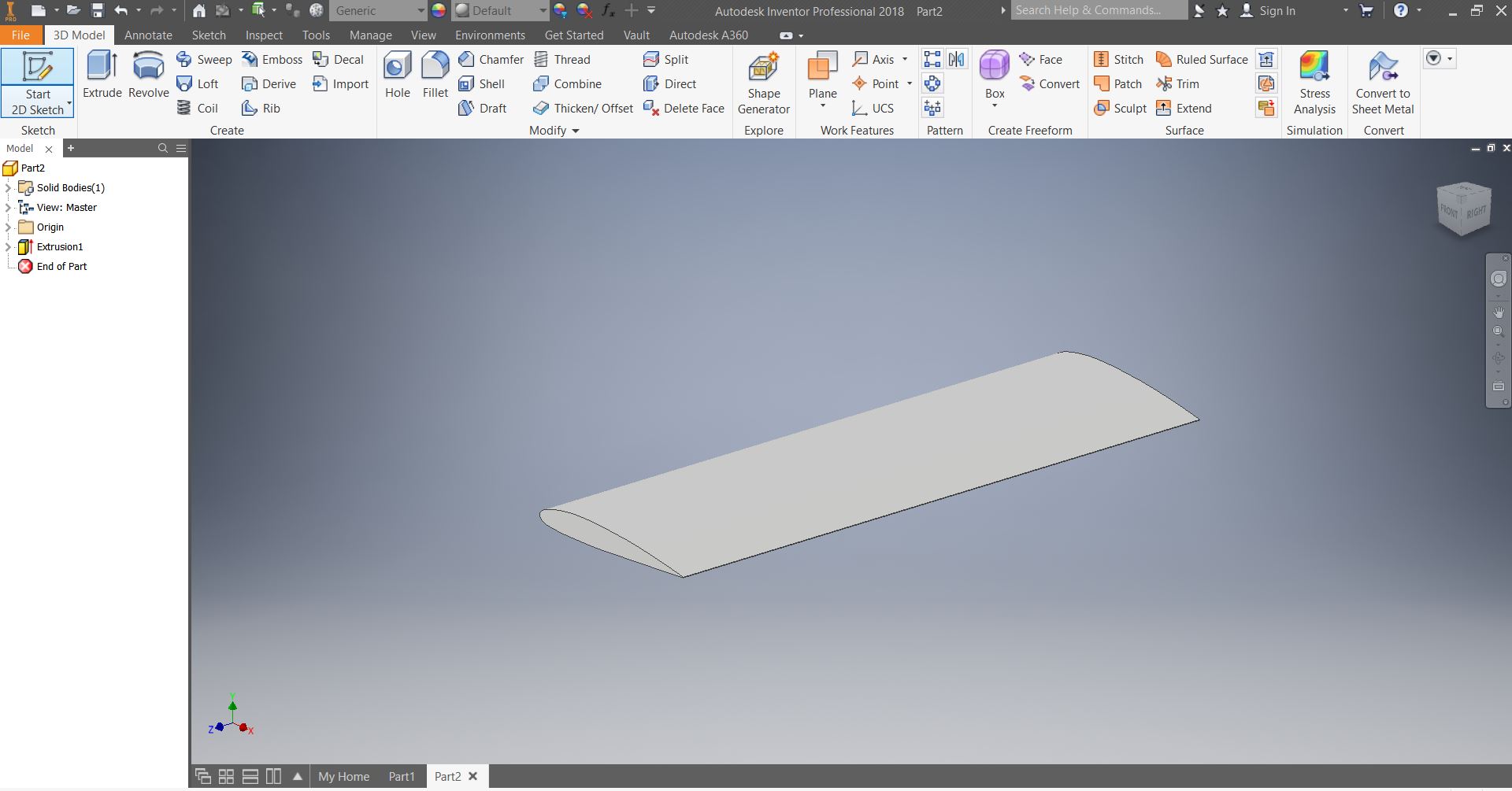
1. Design Airfoil
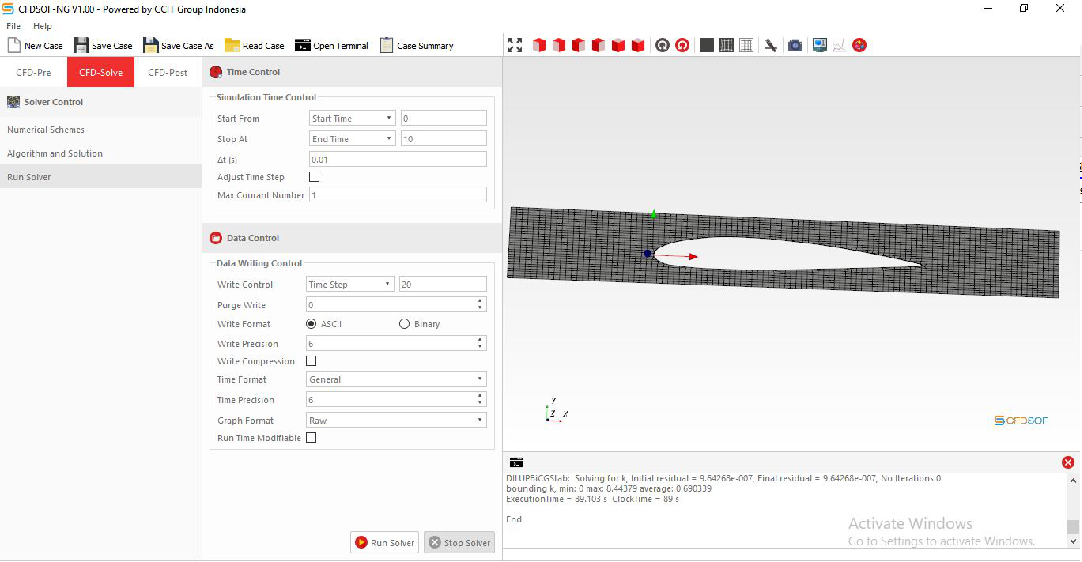
2. Simulasi pada CFDSOF-NG
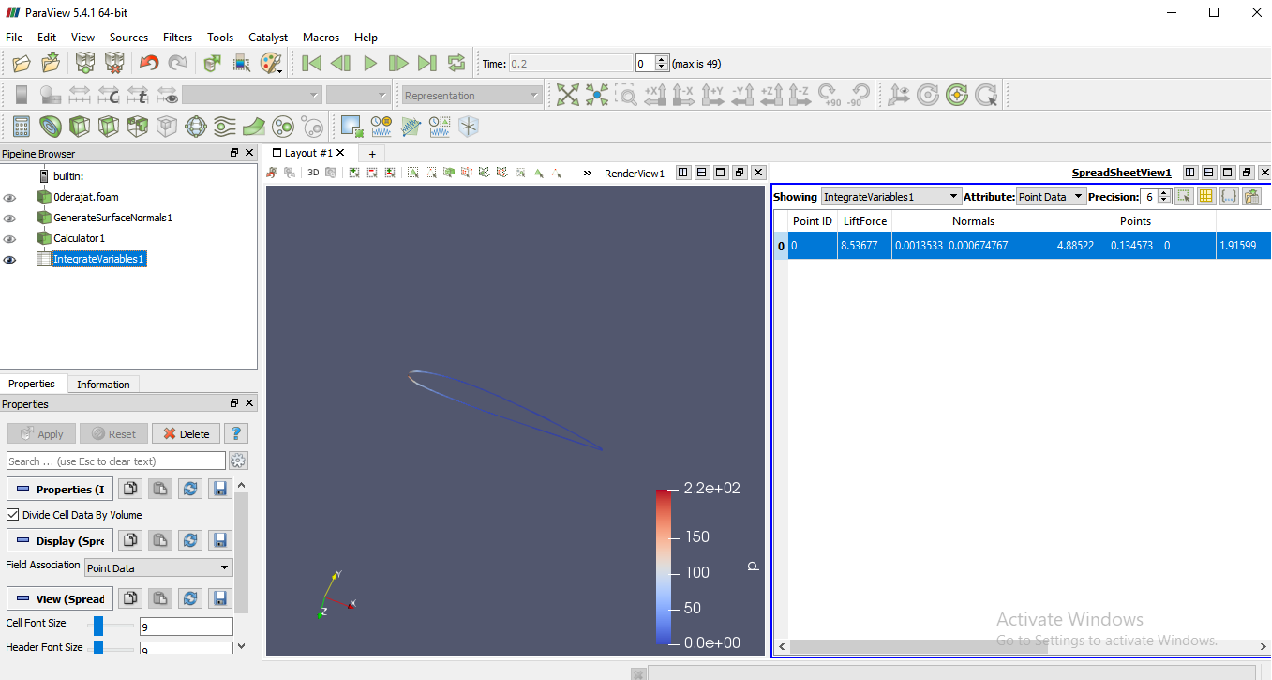
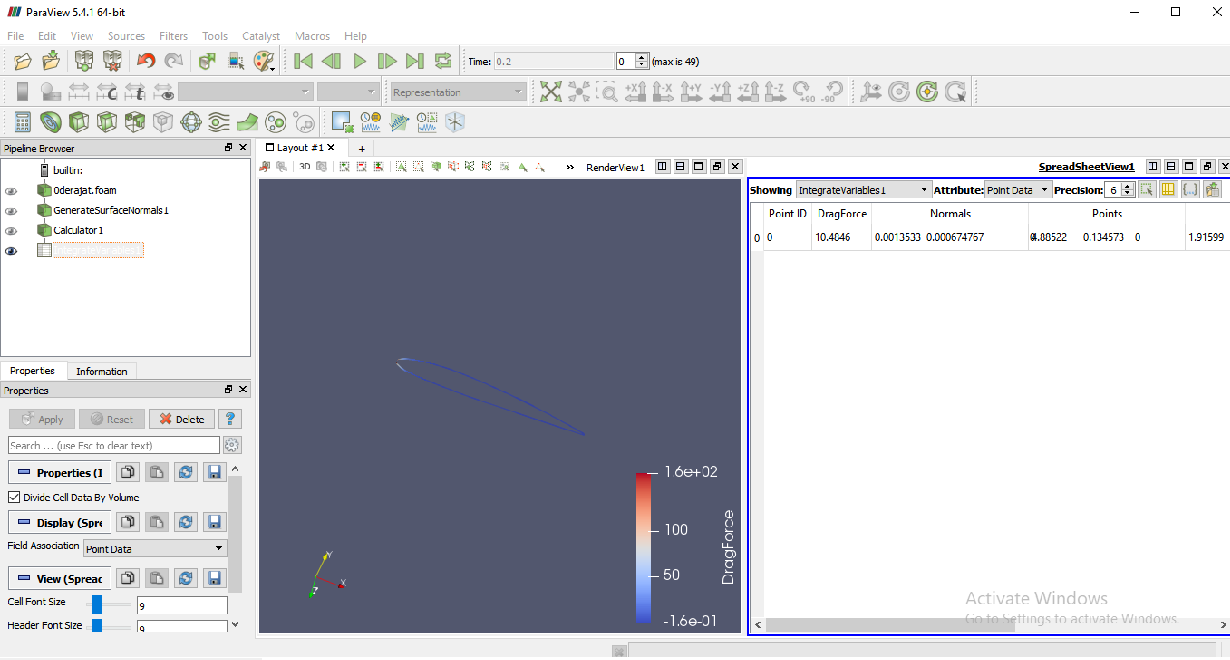
3. Paraview
Lift
Drag
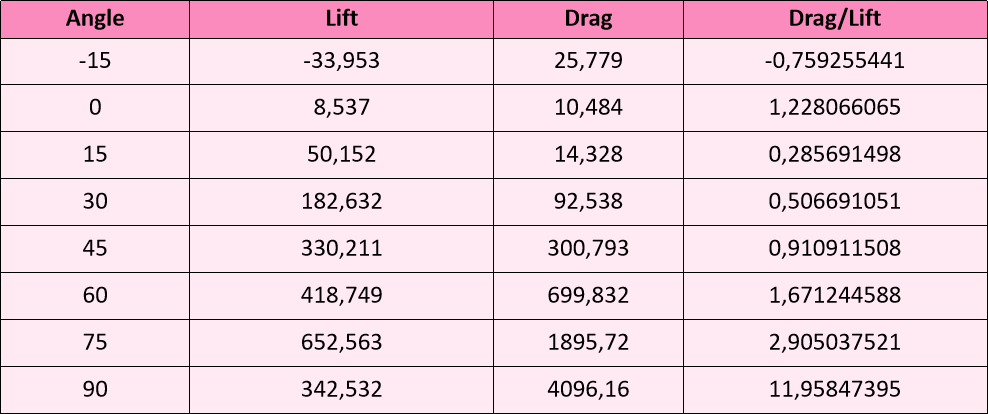
4. Data yang Didapat
Dari hasil yang didapat, buatlah grafik gaya terhadap sudut untuk Drag Force dan Lift Force pada Excel. Dari grafik tersebut didapatkan persamaan grafik yang nanti akan digunakan untuk mengoptimasi sudut Airfoil.
5. Grafik dan Persamaan
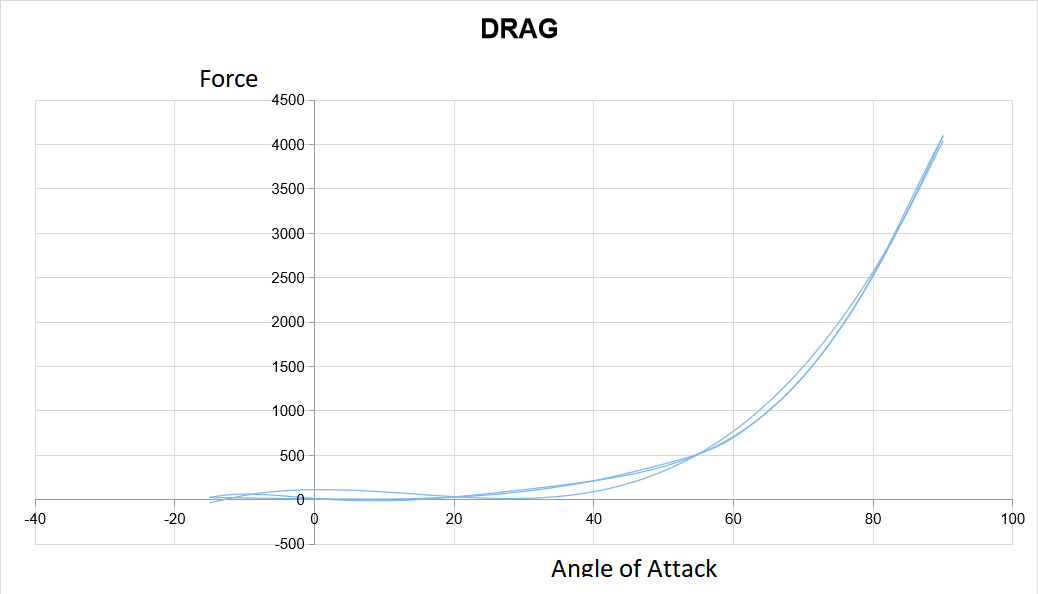
Grafik Drag:
y = 0.0102x3 - 0.4434x2 + 0.8334x + 113.04�R2 = 0.9964
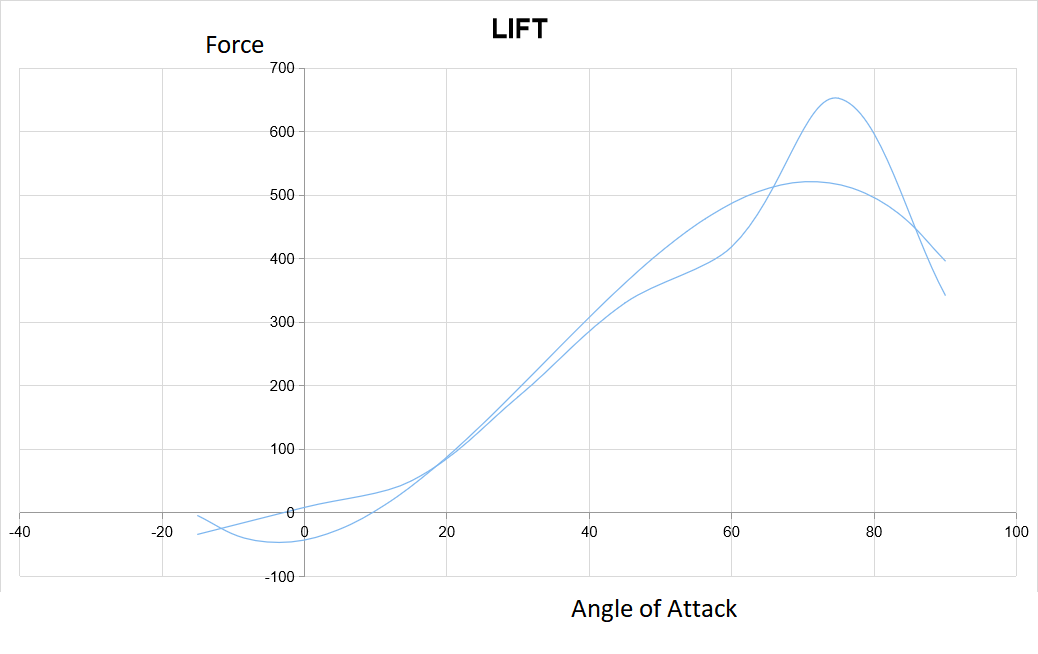
Grafik Lift:
y = -0.0027x3 + 0.2733x2 + 2.1534x - 42.817�R2 = 0.9211
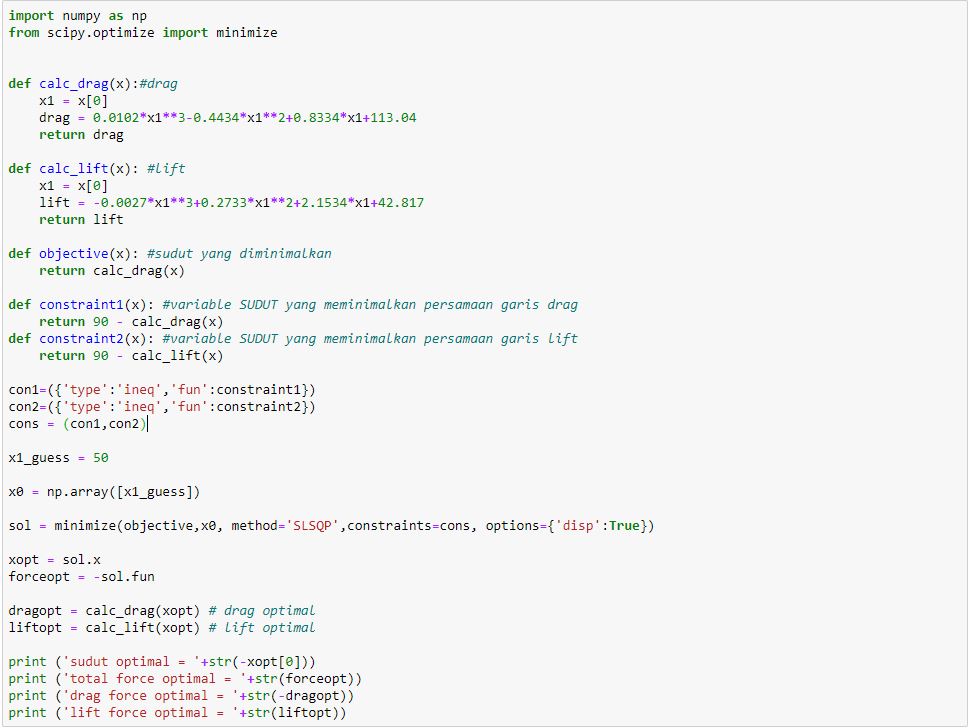
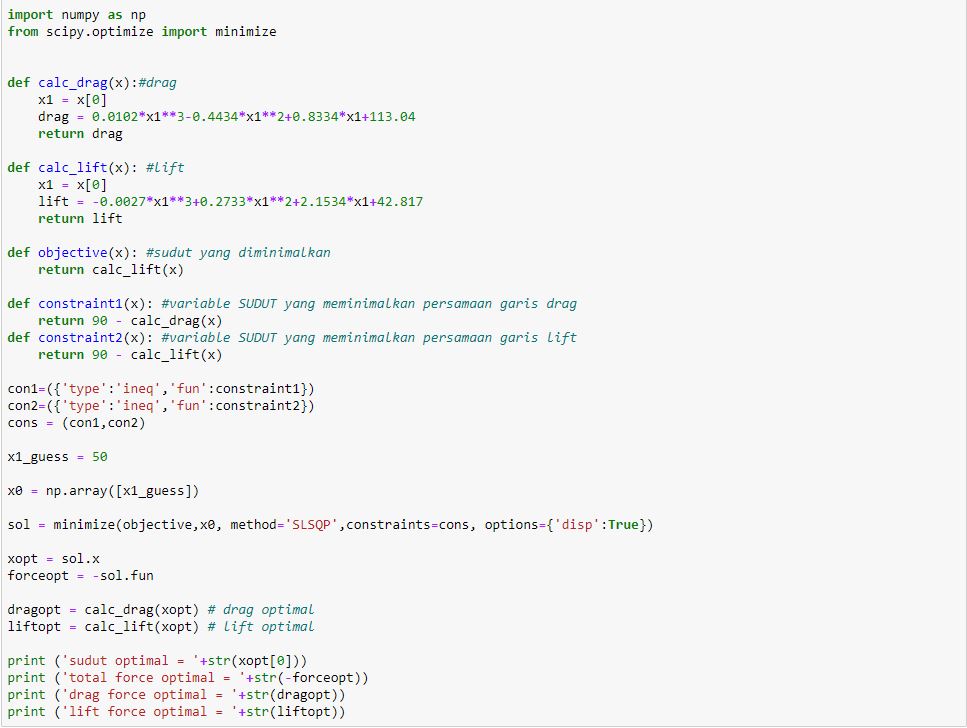
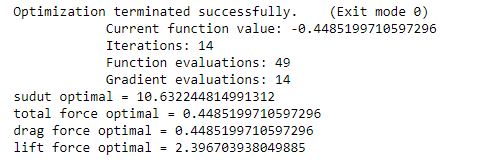
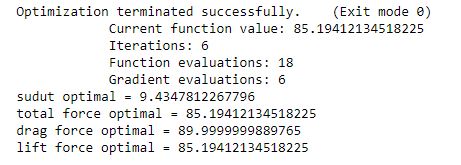
6. Optimasi
7. Hasil dari Optimasi Sudut Airfoil