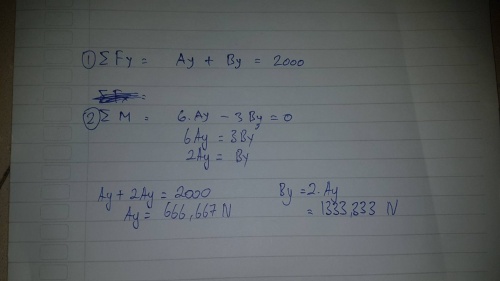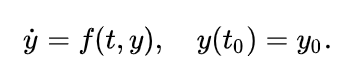Kelompok 6

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

Perkenalkan kami dari kelompok 6 kelas Metode Numerik Kelas Reguler-2

Anggota dari kelompok 6 :

1. Geofany Rosady (1706986366)

2. Jonathan Surya (1706036210)

3. Ronald Galvin (1806200910)

Pendahuluan

Eliminasi Gauss-Jordan adalah integrasi dari eliminasi Gauss yang hasilnya lebih sederhana lagi. Metodenya adalah dengan meneruskan operasi baris dari eliminasi Gauss sampai menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Pada akhirnya ada segitiga atas/ segitiga bawah seperti:

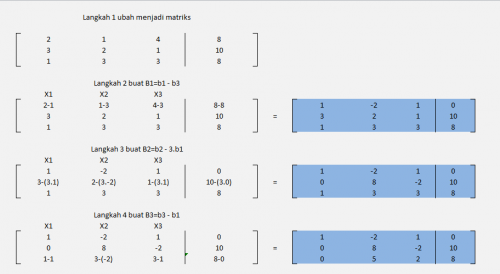
Metode ini digunakan untuk mencari invers dari sebuah matriks. Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah 1. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi. 2. Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks.

Misalkan saja: 2X1 + X2 + 4X3 = 8 3X1 + 2X2 + X3 = 10 X1 + 3X2 + 3X3 = 8

Berikut adalah penyelesaian secara matematis :

Video Tugas Ketiga

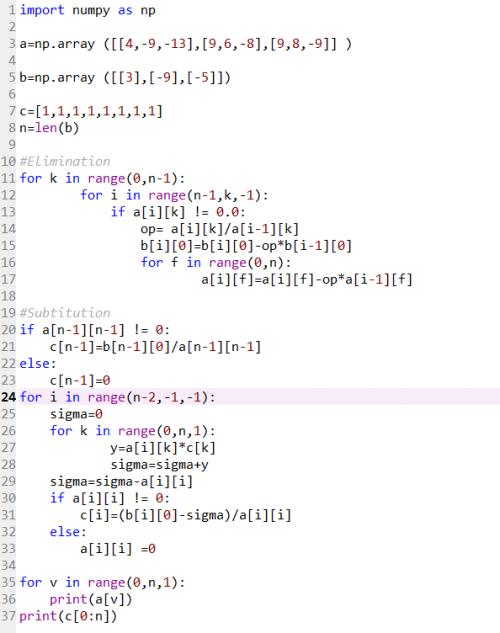
Video diatas merupakan penjelasan penggunaaan aplikasi metode numerik pada eliminasi Gauss. Algortima dari video diatas akan kami tampilkan dibawah ini:

Lalu hasil run sebagai berikut:

Terima Kasih telah membaca blog Wiki kami, jika ingin memberikan pendapat silahkan berkomentar di bawah

Video Tugas Ke-empat

   Tugas keempat adalah mengaplikasikan eliminasi gauss jordan pada penyelesaian soal statistika struktur pada satu dimensi.Salah satu pengaplikasiannya kami mengambil satu contoh yaitu beam yang memiliki 2 tumpuan fix.

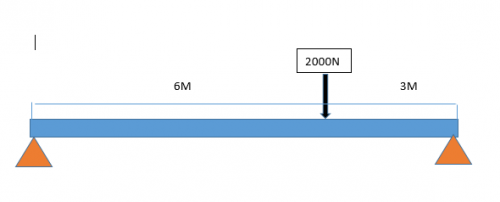
  Panjang total beam L  = 9m, Panjang dari A - gaya = 6m ,Panjang dari B - gaya = 3m, Gaya yang diberikan   = 2000N

berikut gambaran soalnya

berikut contoh penyelesaian manualnya

berikut penyelesaian Pythonnya

Video Tugas Ke-lima

metode Runge-Kutta adalah keluarga metode iteratif implisit dan eksplisit , yang mencakup rutin terkenal yang disebut Metode Euler , yang digunakan dalam diskritisasi temporal untuk solusi perkiraan persamaan diferensial biasa . [1] Metode ini dikembangkan sekitar tahun 1900 oleh matematikawan Jerman Carl Runge dan Wilhelm Kutta

masalah nilai awal ditentukan sebagai berikut:

Berikut hasil pembuatan presentasi dari kelompok kami:

PPT Tugas 5

Video diatas merupakan contoh penyelesaian soal statistika struktur dengan eliminasi gauss jordan

Tugas ke-7

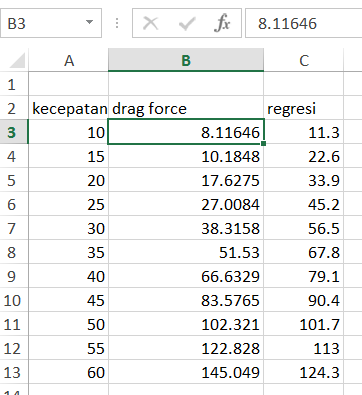
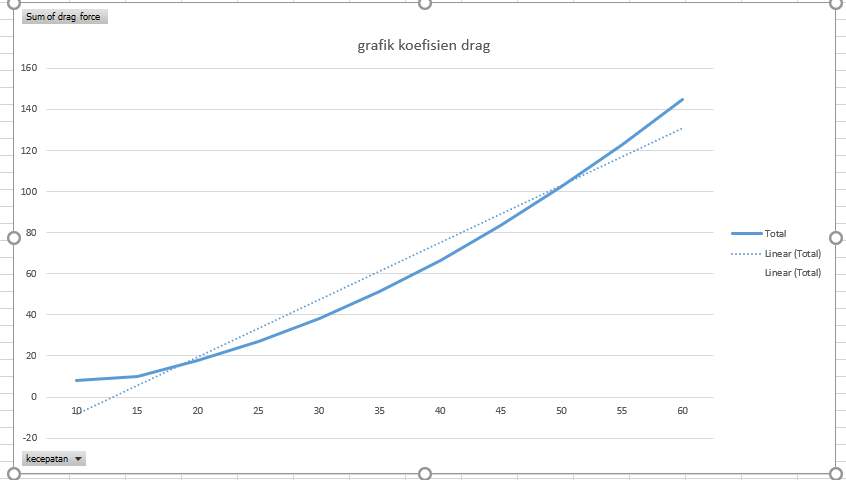
Koefisien drag (Cd) adalah bilangan yang menunjukkan besar kecilnya tahanan fluida yang diterima oleh suatu benda. Harga koefisien drag yang kecil menunjukkan hambatan fluida yang diterima benda saat berjalan adalah kecil, dan begitu juga sebaliknya.

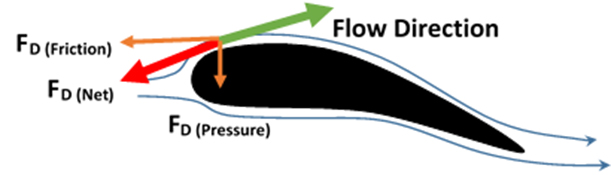
Koefisien seret didefinisikan sebagai:

Fd = gaya drag (definisi komponen gaya dalam arah kecepatan aliran)

p (rho) = massa jenis fluida

v = kecepatan relatif dari objek untuk cairan dan

A = acuan daerah aliran

Semakin kecil angka Cd suatu kendaraan, maka semakin maksimal gerak mobil dan tentunya meningkatkan efisiensi bahan bakar kendaraan.

Sementara itu, nilai koefisien drag yang tinggi bisa berdampak saat mobil bergerak pada kecepatan tinggi. Sebab semakin tinggi angkanya, semakin sulit akselerasi mobil, dan berujung semakin banyak bahan bakar yang digunakan.

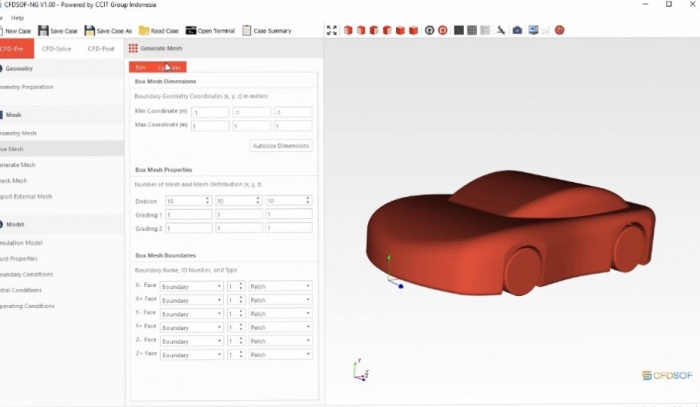
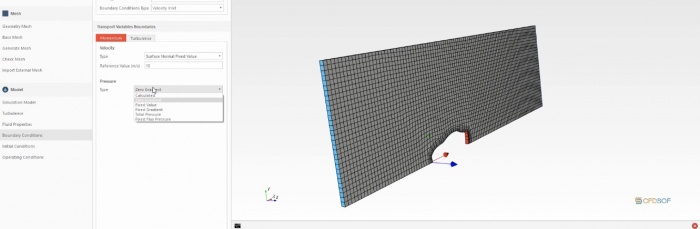
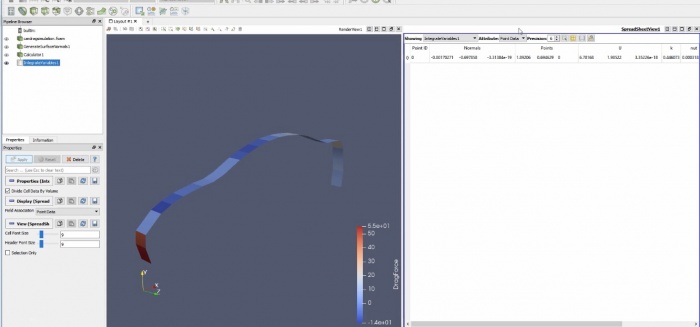
Menghitung Drag Coef. dari mobil menggunakan CFDsof

Tugas ke-8

Airfoil adalah salah satu bentuk bodi aerodinamika sederhana yang berguna untuk dapat memberikan gaya angkat tertentu terhadap suatu bodi lainnya dan dengan bantuan penyelesaian matematis sangat memungkinkan untuk memprediksi berapa besarnya gaya angkat yang dihasilkan oleh suatu bodi airfoil.

Geometri airfoil memiliki pengaruh besar terhadap karakteristik aerodinamika dengan parameter penting berupa CL, dan kemudian akan terkait dengan lift (gaya angkat yang dihasilkan)

Parameter Airfoil: ketebalan maksimum, maksimum bentuk melengkung, posisi max ketebalan, posisi maks bentuk melengkung, dan hidung jari-jari.

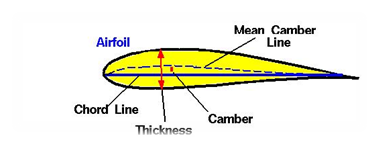
1 . Permukaan atas (Upper Surface)

2 . Permukaan bawah (Lowerer Surface)

3 . Mean camber line adalah tempat kedudukan titik-titik antara permukaan atas dan bawah airfoil yang diukur tegak lurus terhadap mean camber line itu sendiri.

4 . Leading edge adalah titik paling depan pada mean camber line, biasanya berbentuk lingkaran dengan jari-jari mendekati 0,02 c.

5 . Trailing edge adalah titik paling belakang pada mean camber line

6 . Camber adalah jarak maksimum antara mean camber line dan garis chord yang diukur tegak lurus terhadap garis chord.

7 . Ketebalan (thickness) adalah jarak antara permukaan atas dan permukaan bawah yang diukur tegak lurus terhadap garis chord.

Pada airfoil terdapat beberapa bagian yang dirubah untuk mendapat koefisien gaya angkat yang maksimal, diantaranya camber.

Semakin besar camber suatu airfoil maka semakin besar gaya angkat yang akan dihasilkan oleh sebuah airfoil, karena perubahan arah angin di trailing edge menyebabkan semakin besar gaya angkatnya.

Hal itu juga disebabkan karena prinsip dasar airfoil adalah untuk mempecepat kecepatan angin di bagian atas dengan memperpanjang daerah lintasan airfoil dan memperpendek lintasan bagian bawah airfoil sehingga perbedaan tekanan permukaan atas dan bawah makin besar maka gaya angkat yang dihasilkan makin besar pula

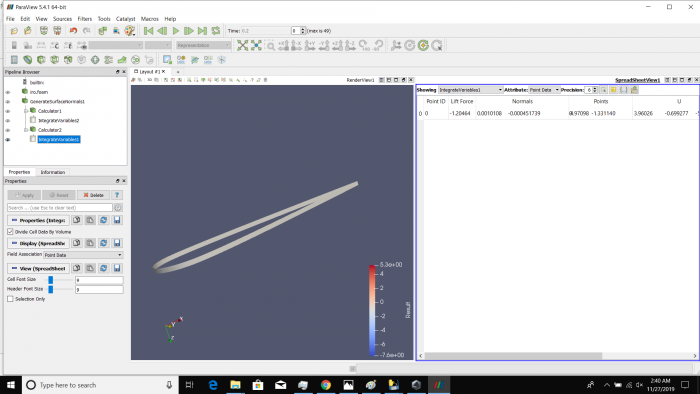
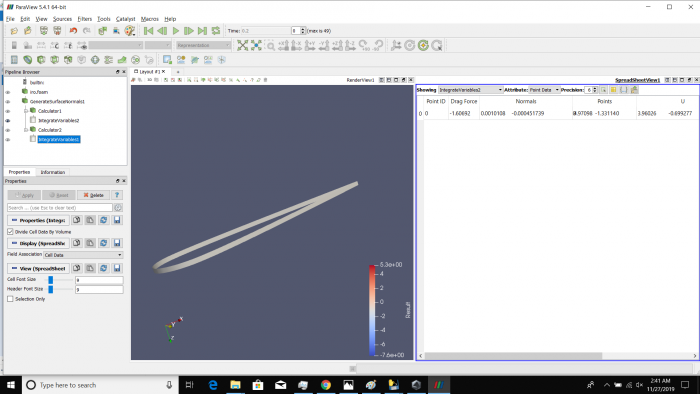
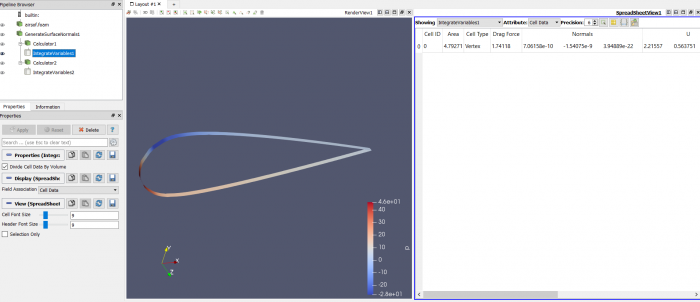
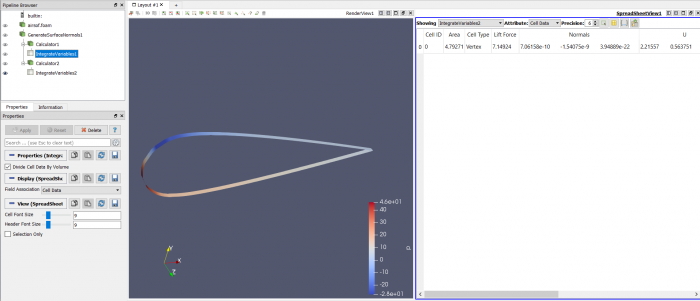
Pada tugas hari ini, kami diberikan suatu tugas untuk mencari hubungan antara sudut serang (angle of attack) dan gaya drag&lift yang terjadi pada suatu bentuk airfoil yang 
kita design sendiri. Untuk mengerjakan tugas ini, Kami menyusun tahap-tahap pengerjaan sebagai berikut:

1. Mendesain airfoil dengan menggunakan Inventor/ Solidworks dan disimpan dalam bentuk .stl

2. Menggunakan CFDSOF untuk menganalisis aliran fluida dengan parameter-parameter yang telah ditetapkan

3. Menggunakan excel untuk membuat Plot hasil dan Curve fitting

4. Melakukan optimasi dengan menggunakan Phyton

5. Hasil dan Kesimpulan

Untuk itu berikut ini akan kami bahas tiap detil dari langkah-langkah tersebut sebagai berikut:

Mendesain airfoil dengan menggunakan software Inventor

Kelompok kami memutuskan menggunakan airfoil sebuah pesawat yang diperkecil ukuranya agar pada proses generate mesh tidak terlalu lama. Lalu kami simpan dalam bentuk .stl, setelahnya kami simpan pada folder tugas.

Analisis fluida dengan software CFD-SOF

Parameter yang kami gunakan: - Kecepatan 10 m/s - Mesh: dan mendapatan hasil data drag&lift Force dari setiap sudut serang dari -15 sampai 90 derajat dengan kelipatan sudut adalah 15

Plot hasil dan curve fitting

Optimasi dengan menggunakan Phyton

-masih dalam proses

Kesimpulan

Soal mencari coefficient drag pada sudut serang 15,30,45,60,75,90.

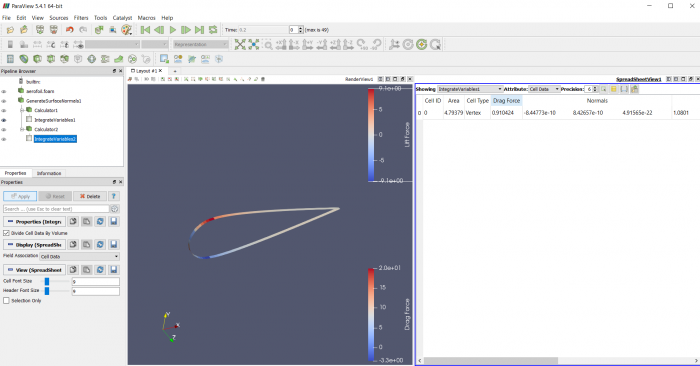
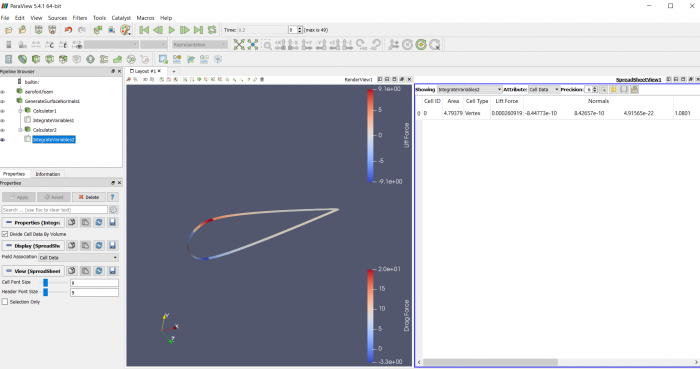
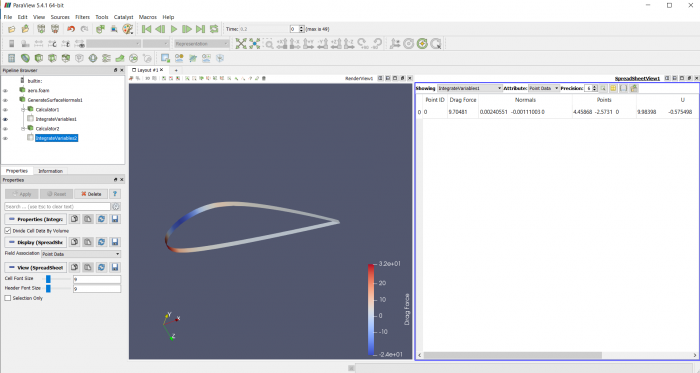
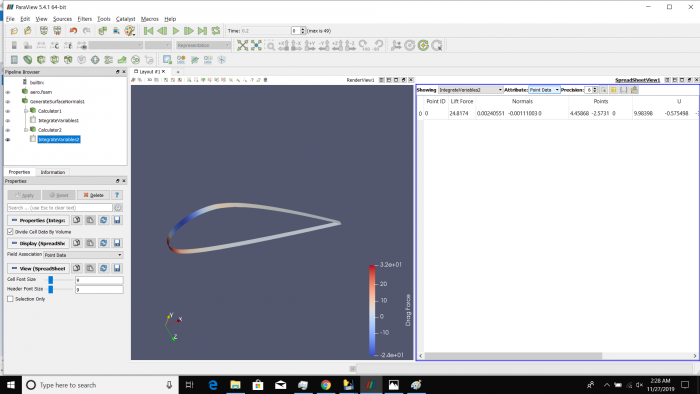
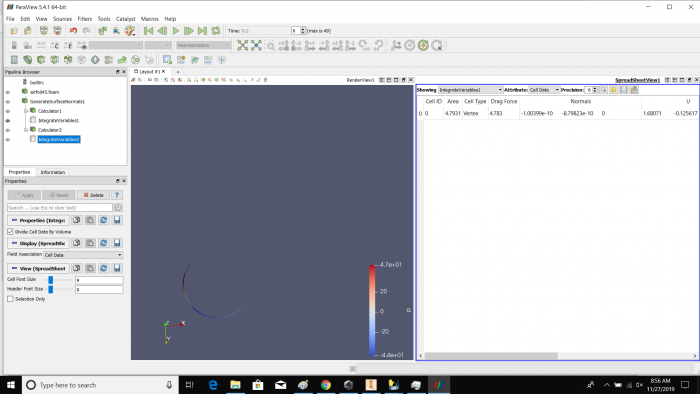
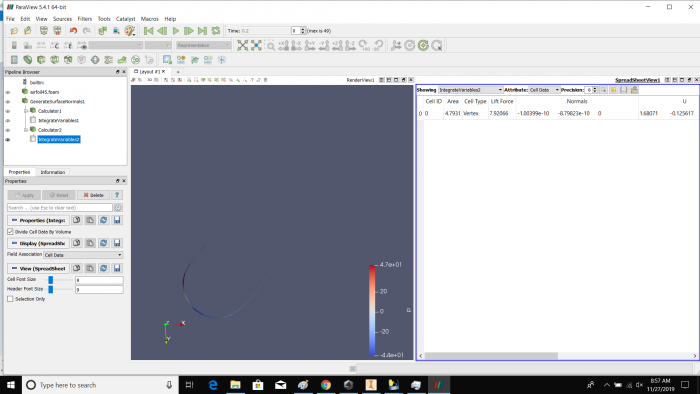
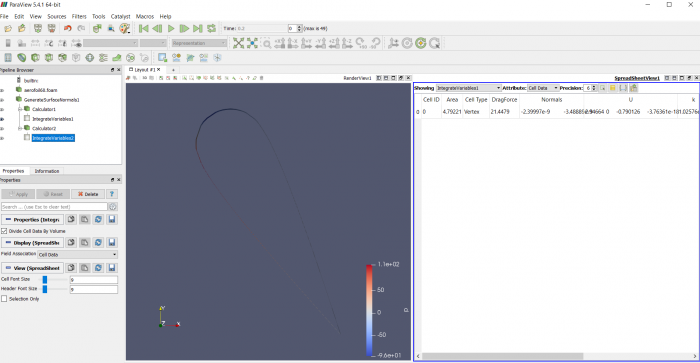
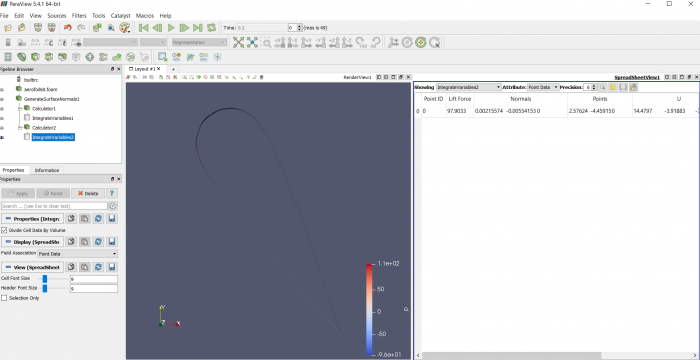
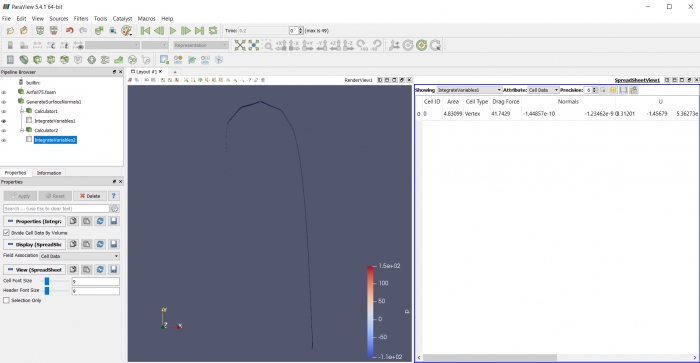
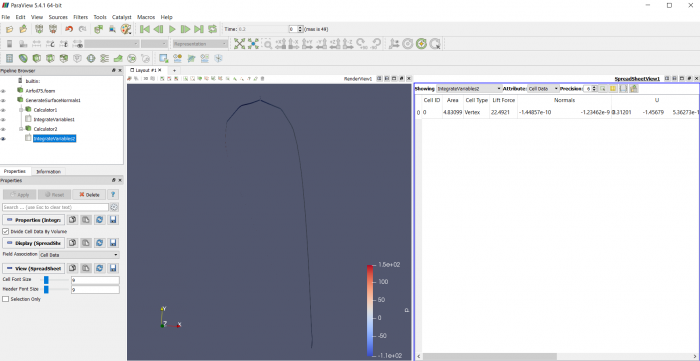
Airfoil pada sudut +15 derajat

Airfoil pada sudut 0 derajat

Airfoil pada sudut -15 derajat

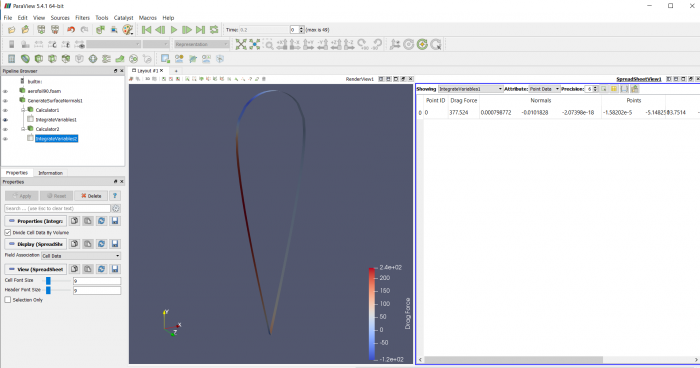
Airfoil pada sudut +30 derajat

Airfoil pada sudut +45 derajat

Airfoil pada sudut +60 derajat

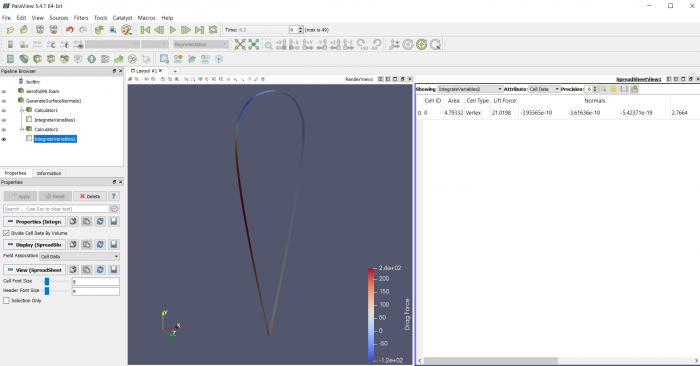
Airfoil pada sudut +75 derajat

Airfoil pada sudut +90 derajat

Proses simulasi dengan CFDSOF

pertama dalam

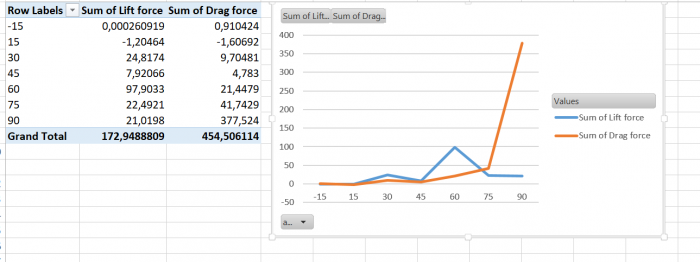
   Grafik AirFoil Drag Force dan Lift Force

Grafik gabungan drag dan lift dari airfoil. Dimana drag force semakin bertambah besar seiring naiknya sudut serang. sedangkan nilai Lift diperoleh optimumnya pada sudut serang 60

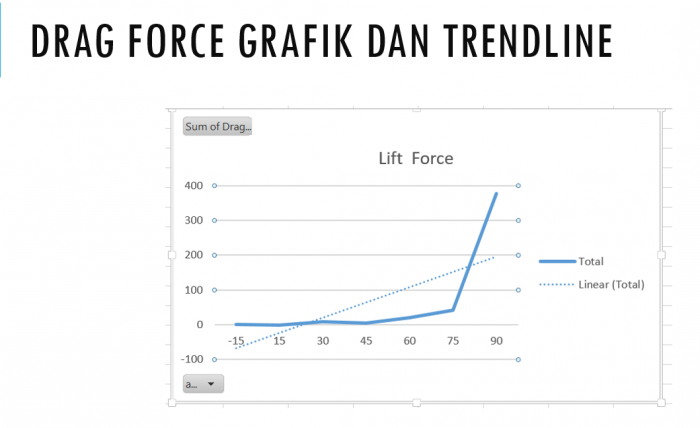
Grafik Drag Force dengan trendline nilai linear y= 43,867x-110,54 Grafik Drag Force dengan trendline nilai polinomial y= 21,185x^2-125,62x + 143,69

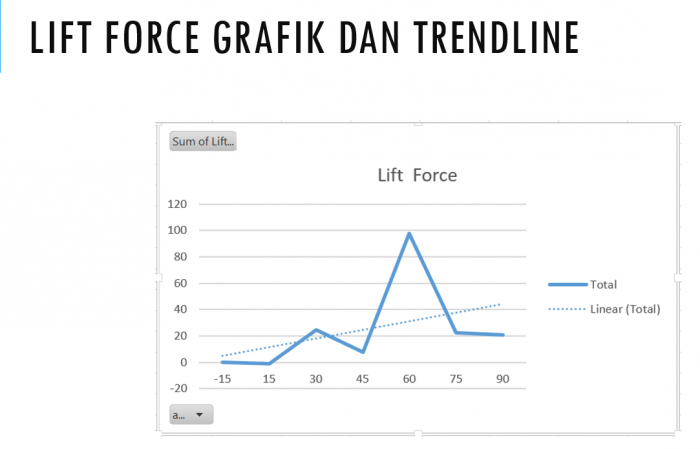
Grafik Lift Force dengan trendline nilai linear y= 6,5549x-1,5127 Grafik Lift Force dengan trendline nilai polinomial y= -3,5089x^2 + 34,626x - 43,619

Optimasi