Kelompok 6
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Perkenalkan kami dari kelompok 6 kelas Metode Numerik Kelas Reguler-2
Anggota dari kelompok 6 :
1. Geofany Rosady (1706986366)
2. Jonathan Surya (1706036210)
3. Ronald Galvin (1806200910)
Contents
Pendahuluan
Eliminasi Gauss-Jordan adalah integrasi dari eliminasi Gauss yang hasilnya lebih sederhana lagi. Metodenya adalah dengan meneruskan operasi baris dari eliminasi Gauss sampai menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Pada akhirnya ada segitiga atas/ segitiga bawah seperti:
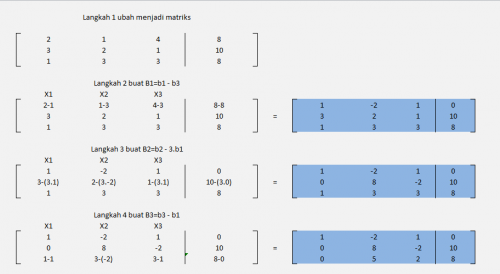
Metode ini digunakan untuk mencari invers dari sebuah matriks. Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah 1. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi. 2. Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks.
Misalkan saja: 2X1 + X2 + 4X3 = 8 3X1 + 2X2 + X3 = 10 X1 + 3X2 + 3X3 = 8
Berikut adalah penyelesaian secara matematis :
Video Tugas Ketiga
Video diatas merupakan penjelasan penggunaaan aplikasi metode numerik pada eliminasi Gauss. Algortima dari video diatas akan kami tampilkan dibawah ini:
Lalu hasil run sebagai berikut:
Terima Kasih telah membaca blog Wiki kami, jika ingin memberikan pendapat silahkan berkomentar di bawah
Video Tugas Ke-empat
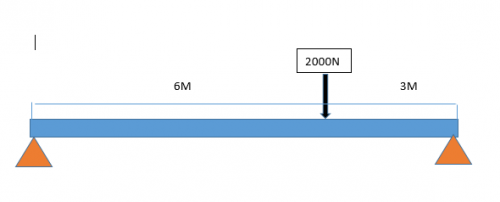
Tugas keempat adalah mengaplikasikan eliminasi gauss jordan pada penyelesaian soal statistika struktur pada satu dimensi.Salah satu pengaplikasiannya kami mengambil satu contoh yaitu beam yang memiliki 2 tumpuan fix.
Panjang total beam L = 9m, Panjang dari A - gaya = 6m ,Panjang dari B - gaya = 3m, Gaya yang diberikan = 2000N
berikut gambaran soalnya
berikut contoh penyelesaian manualnya
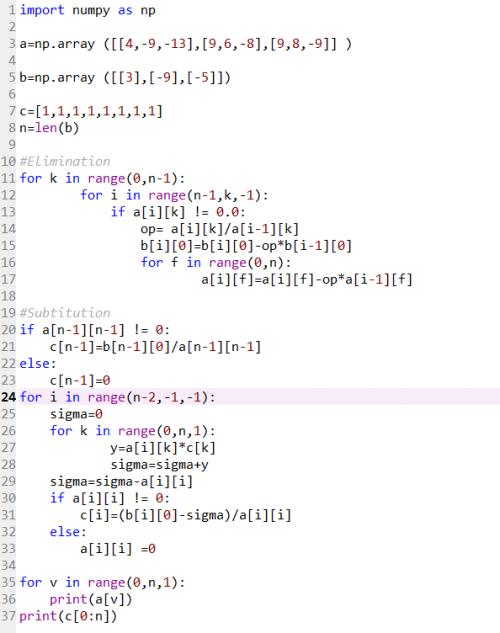
berikut penyelesaian Pythonnya
Video Tugas Ke-lima
metode Runge-Kutta adalah keluarga metode iteratif implisit dan eksplisit , yang mencakup rutin terkenal yang disebut Metode Euler , yang digunakan dalam diskritisasi temporal untuk solusi perkiraan persamaan diferensial biasa . [1] Metode ini dikembangkan sekitar tahun 1900 oleh matematikawan Jerman Carl Runge dan Wilhelm Kutta
masalah nilai awal ditentukan sebagai berikut:
Berikut hasil pembuatan presentasi dari kelompok kami:
Video diatas merupakan contoh penyelesaian soal statistika struktur dengan eliminasi gauss jordan
Tugas ke-7
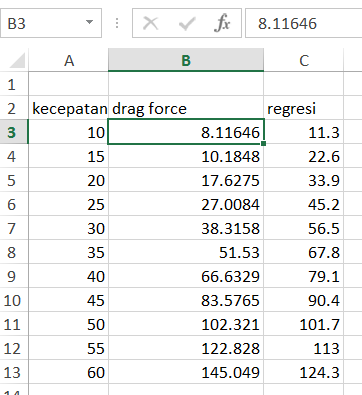
Koefisien drag (Cd) adalah bilangan yang menunjukkan besar kecilnya tahanan fluida yang diterima oleh suatu benda. Harga koefisien drag yang kecil menunjukkan hambatan fluida yang diterima benda saat berjalan adalah kecil, dan begitu juga sebaliknya.
Koefisien seret didefinisikan sebagai:
Fd = gaya drag (definisi komponen gaya dalam arah kecepatan aliran) p (rho) = massa jenis fluida v = kecepatan relatif dari objek untuk cairan dan A = acuan daerah aliran
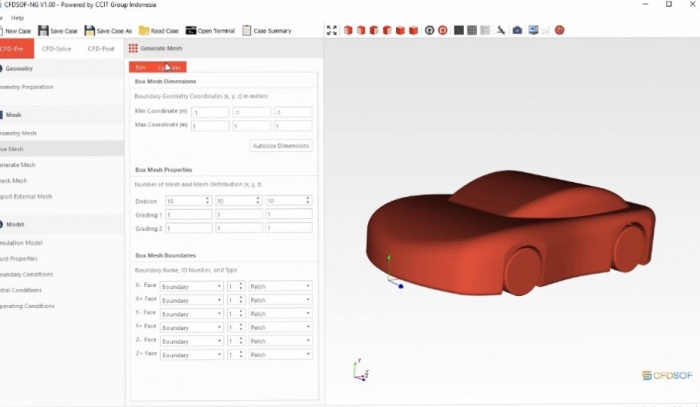
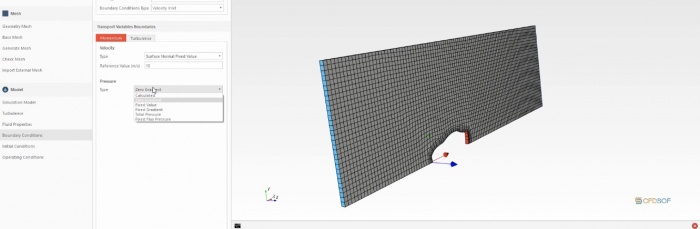
Menghitung Drag Coef. dari mobil menggunakan CFDsof
Tugas ke-8
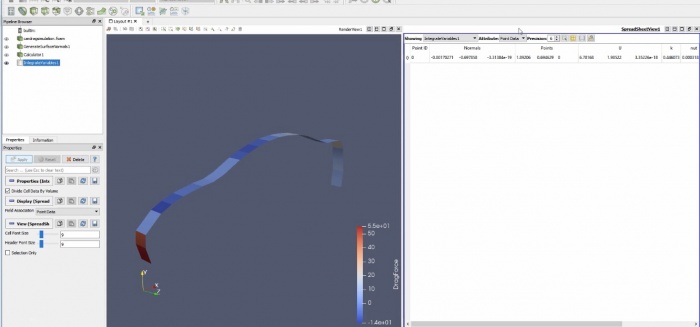
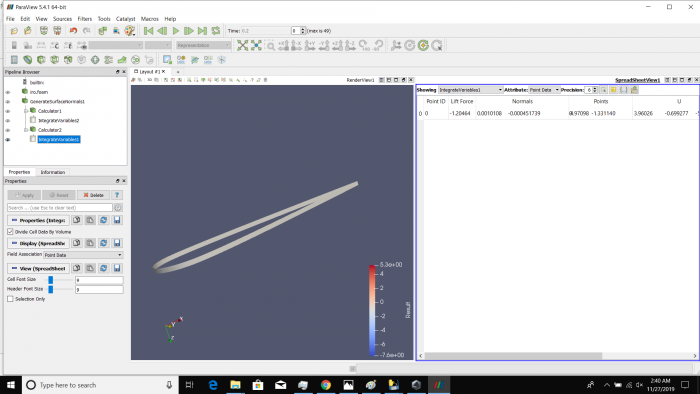
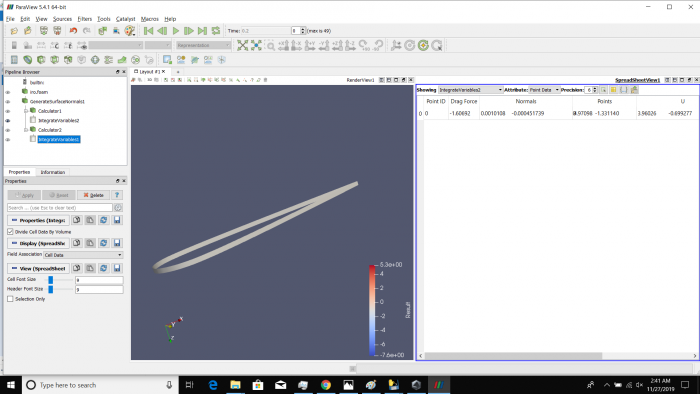
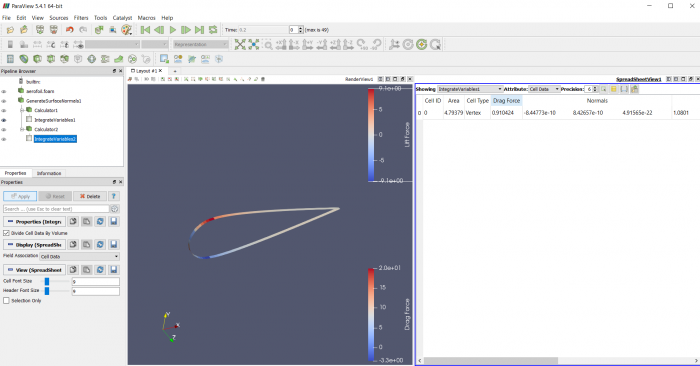
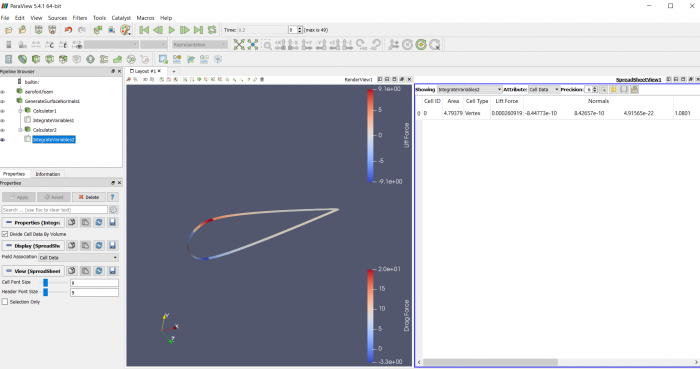
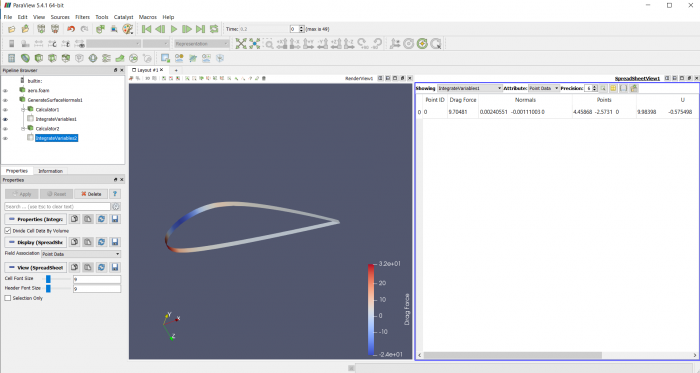
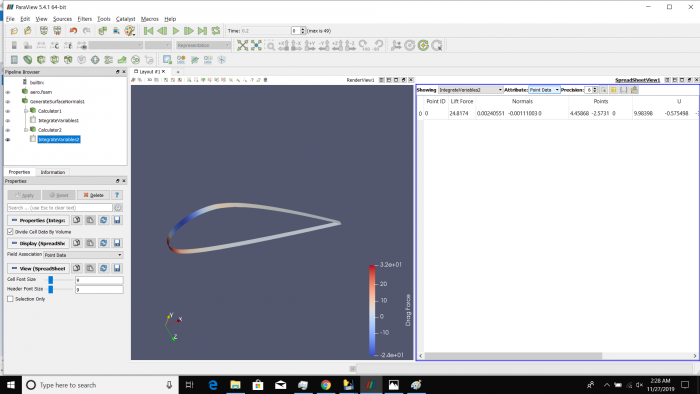
Airfoil pada sudut +15 derajat
Airfoil pada sudut -15 derajat
Airfoil pada sudut +30 derajat





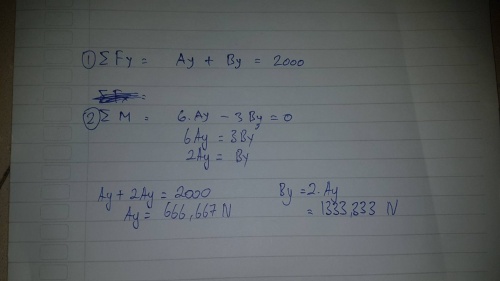
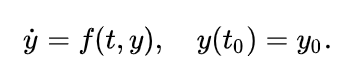

Enable comment auto-refresher
Jonathan.Surya
Permalink |
Geofany.rosady
Permalink |