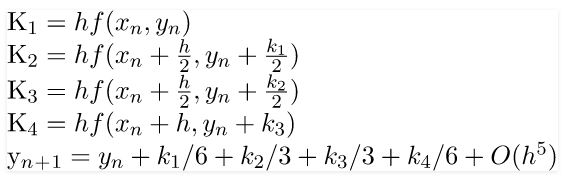Hervin

Profil

Nama: Hervin

NPM: 186200923

Jurusan: Teknik Mesin, angkatan 2018

Semester 1

Pertemuan 1: Selasa, 2 September 2019

Metode Numerik

Dalam Matematika, terdapat cara untuk menyelesaikan persoalan, seperti Metode Analitik (Eksak) dan Metode Numerik. Metode Numerik ialah metode yang digunakan apabila metode eksak tidak dapat digunakan dalam suatu persoalan, seperti yang sudah diterapkan dalam mata kuliah Kalkulus 1 dan 2, Aljabar Linear, dan Matematika Teknik. Metode Numerik mengandalkan daya kerja komputer yang mampu mengolah persoalan kompleks secara cepat dan efisien waktu. Pada pertemuan ini, Metode Numerik akan diterapkan dan dipelajari di dalam Microsof Excel.

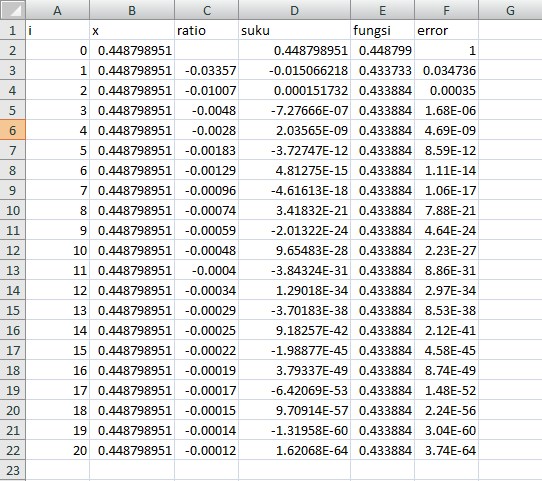
Penerapan di Excel mengambil contoh dengan deret yang sudah dipelajari di Kalkulus 2, yaitu Deret Taylor dan MacLaurin. Contoh ini digunakan dengan dasar bahwa dibalik Deret Taylor dan MacLaurin, terdapat pola algoritma yang dapat di-input dalam perhitungan komputer untuk diproses.

Dengan: x = π/7

ratio (C3)= -1*B2^2/((2*A3)*(2*A3+1))

suku (D3) = D2*C3

fungsi (E3) = E2+D3

error (F3) = ABS(D4/E4)

SETELAH UTS

TUGAS 1: GOVERNING EQUATION

Dalam kelas, diberi tugas untuk menentukan berapa lama waktu yang diperlukan oleh suatu mobil untuk mencapai kecepatan maksimumnya apabila mobil bergerak di lantai kasar dan terapat hambatan udara. Model matematika yang digunakan ialah menggunakan Hukum ke-2 Newton untuk mendapatkan persamaan yang bergantung pada waktu. Untuk memprosesnya, digunakan metode Runge-Kutta Method 4th Order yang kemudian akan dimasukkan ke dalam bahasa pemrograman. Di sini kelompok saya sudah mengsketsa diagram benda bebas serta persamaan yang sudah diturunkan dan pseudo-code yang diperlukan

INSERT FILE HERE

Runge-Kutta Method sendiri ialah metode yang mengandalkan aplikasi repetisi kepada suatu persamaan untuk mendapatkan akurasi yang lebih tinggi selama repetisi tetap digunakan. Runge-Kutta 4th Order ialah Runge-Kutta yang menggunakan 4 repetisi, dengan persamaan umum sebagai berikut: