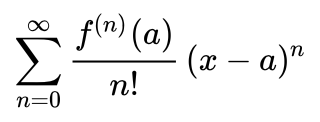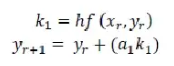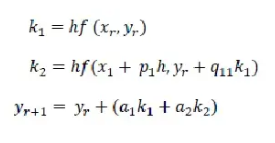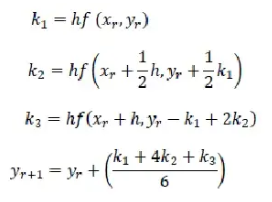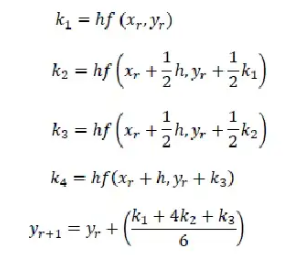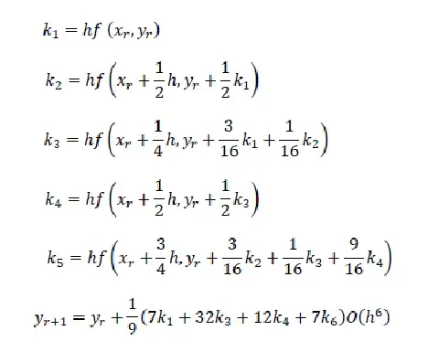Fanya Mellinda Salsabila

Profil

Nama: Fanya Mellinda Salsabila

NPM: 1706036141

Jurusan: Teknik Mesin

Pertemuan Pertama (03 September 2019)

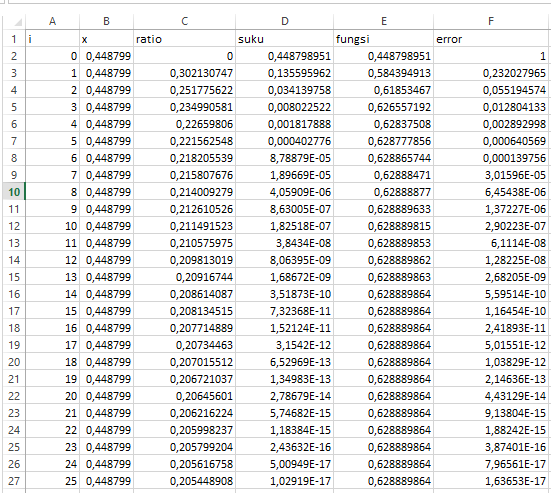
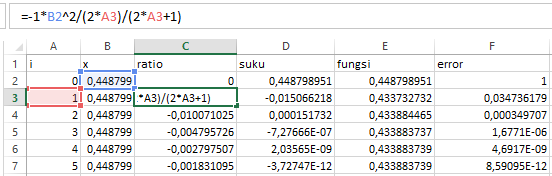
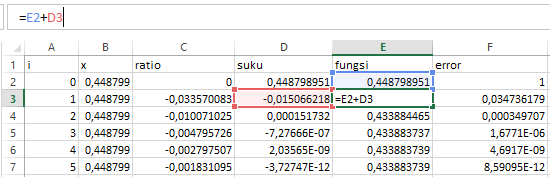
Pada pertemuan pertama mata kuliah Metode Numerik, kami mempelajari cara menghitung nilai-nilai sin x, cos x, e^x, log x atau ln(x+1) menggunakan metode numerik dengan cara Deret Taylor atau Deret MacLaurin. Nilai-nilai tersebut akan rumit dihitung secara manual, maka dari itu dibutuhkan bantuan seperti kalkulator, Microsoft Excel, software programming atau tabel untuk menghitung nilai dari fungsi-fungsi tersebut. Pada pertemuan kali ini, kami diberi latihan menggunakan Microsoft Excel dengan langkah-langkah sebagai berikut:

Dengan:

i = 0-25

x = pi/7

Rumus-rumus:

1. Ratio

Ratio merupakan penyerdehanaan dari rumus deret taylor sebagai berikut:

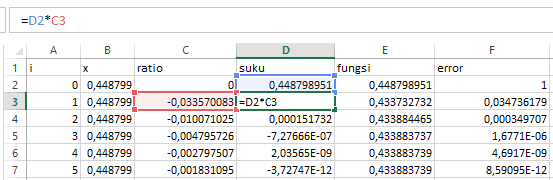
2. Suku

3. Fungsi

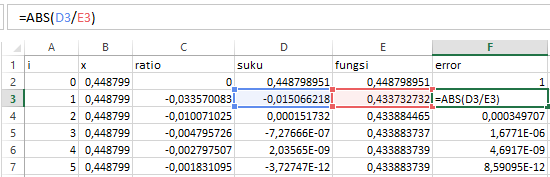
4. Error

Pertemuan Kedua (10 September 2019)

Pseudocode

Pseudocode adalah deskripsi tingkat tinggi informal dan ringkas atas algoritma pemrograman komputer yang menggunakan konvensi struktural atas suatu bahasa pemrograman, dan ditujukan untuk dibacaoleh manusia dan bukan oleh mesin. Pseudocode merupakan kode yang mirip dengan pemograman sebenarnya.

Pseudocode berasal dari kata Pseudo yang berarti imitasi, mirip, atau menyerupaidengan kode bahasa pemograman. Dalam penulisan pseudocode tidak ada aturan yang baku, oleh karena itu pseudocode biasanya ditulis berbasiskan bahasa pemograman yang akan digunakan, misalnya Basic, pascal, C++ dan lain-lain. Sehingga lebih tepat digunakan untukmenggambarkan algoritma yang akan dikomunikasikan kepada programmer.

Kami diberikan latihan untuk mencari nilai dari sin x, cos x, dan e^x sebagai berikut:

Pertemuan Ketiga (17 September 2019)

Turunan Numerik

Metode numerik digunakan untuk menyelesaikan persamaan-persamaan diferensial (dan juga integral) yang kompkleks. Pendekatan numerik diperlukan untuk menyelesaikan persamaan diferensial tersebut dengan mencari hampiran turunannya terlebih dahulu. Salah satu metode yang biasa digunakan untuk menghitung hampiran turunan adalah metode beda hingga (finite difference).

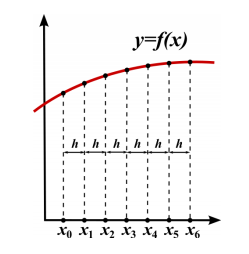
Pada metode beda hingga, domain fungsi f (x) dipartisi atas sejumlah titik partisi dengan lebar selang yang sama. Domain f (x), misalkan [a, b], dipartisi atas N + 1 titik partisi dengan lebar selang h. Dengan demikian titik-titik partisinya adalah:

xi = a + ih, i = 0, 1, ..., N.

Dalam hal ini x0 = a dan xN = b.

Selanjutnya nilai fungsi di masing-masing titik partisi ditulis fi = f (xi)

Ilustrasi untuk N = 6:

Ada tiga jenis beda hingga yang biasa digunakan:

1. Beda maju (forward difference)

Hampiran menggunakan informasi di titik xi dan beberapa titik di kanannya, yaitu xi+1, xi+2, ....

2. Beda mundur (back difference)

Hampiran menggunakan informasi di titik xi dan beberapa titik di kirinya, yaitu ..., xi−2, xi−1.

3. Beda pusat/tengah (central difference)

Hampiran menggunakan informasi di titik xi dan beberapa titik di kiri dan kanannya secara simetris (sama banyak).

Pertemuan Keempat (24 September 2019)

Root-Finding Problems

Root finding problem adalah sebuah persoalan untuk mencari akar dari persamaan f(x) = 0, dimana f(x) merupakan fungsi dari variabel tunggal x. Persoalan tersebut secara spesifik dinyatakan sebagai berikut:

Pertemuan 29 Oktober 2019

Python

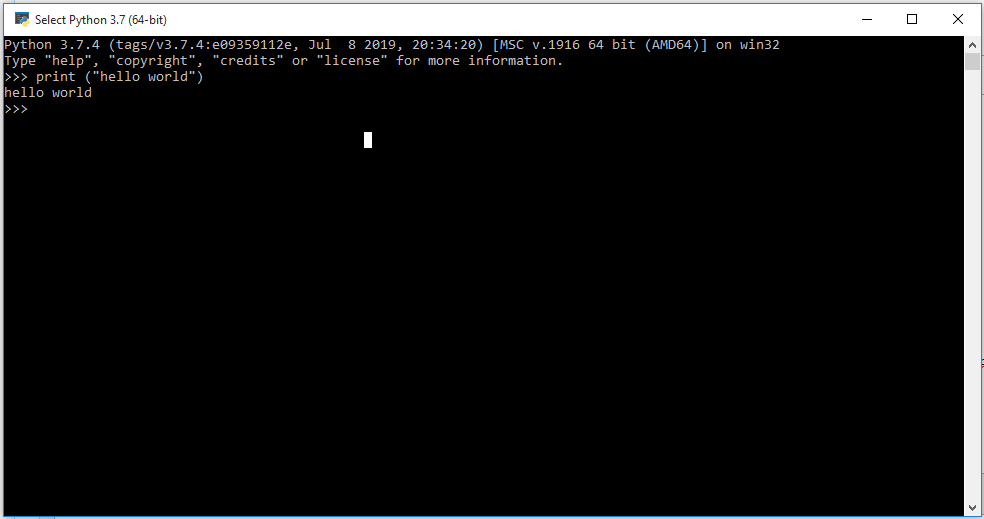
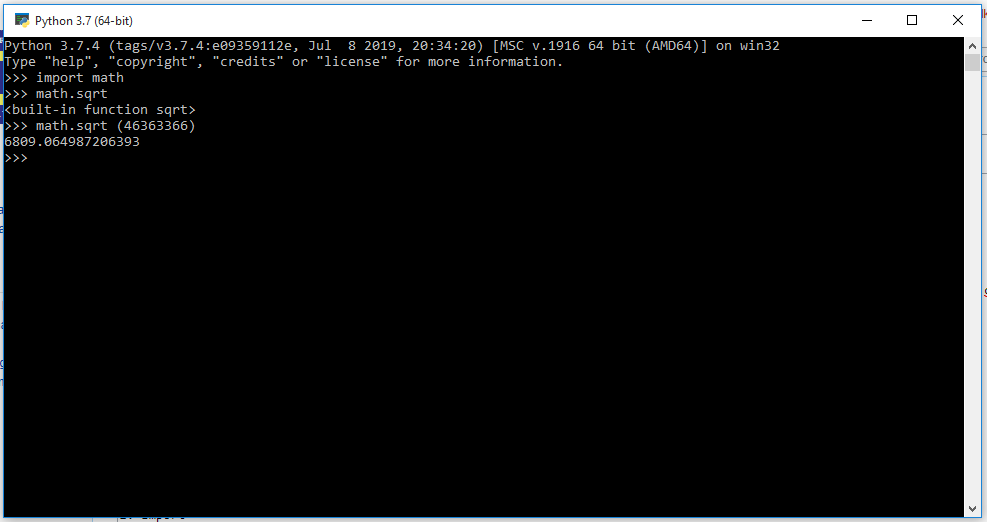
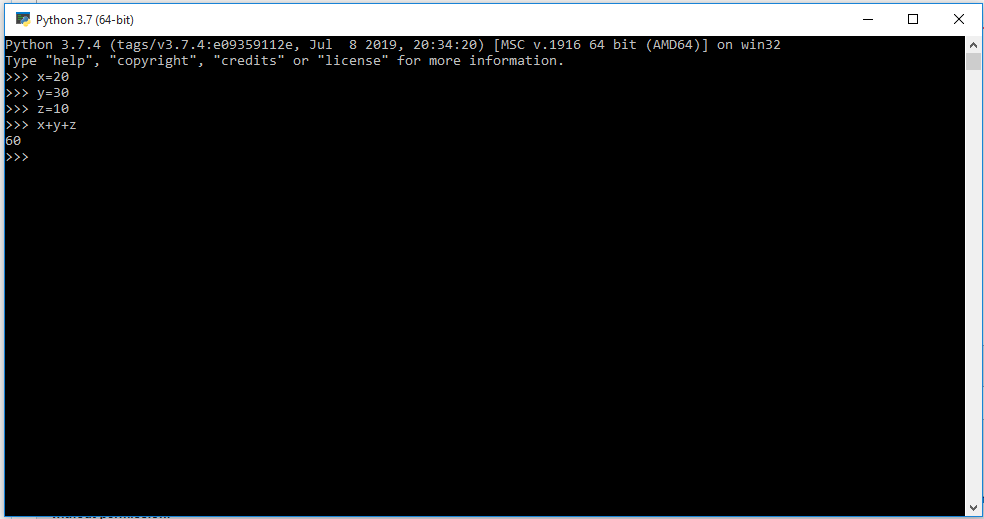
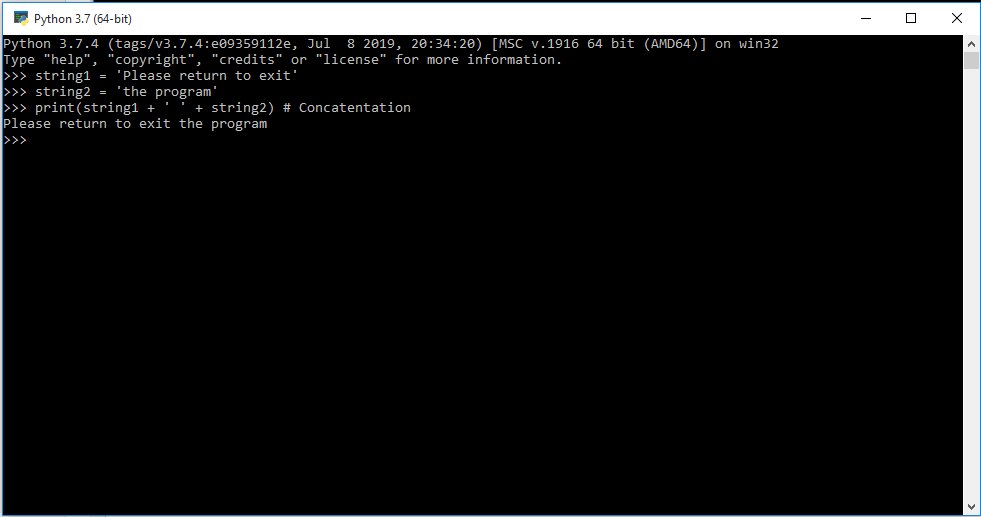
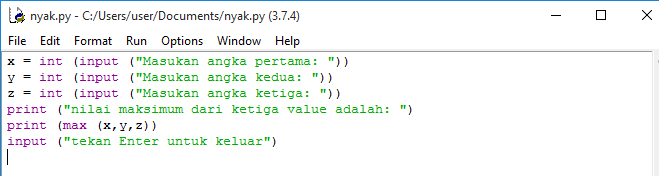
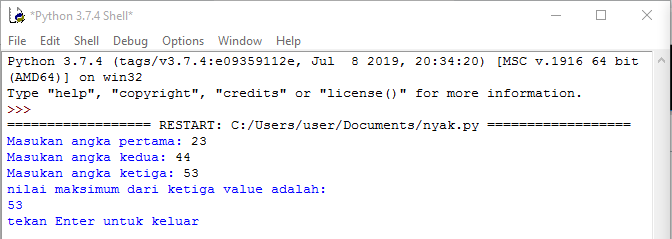
Pada pertemuan hari ini tentang bagaimana cara menggunakan aplikasi Python. Dengan mencoba hal-hal di bawah ini:

1. Print

2. Import

3. Memasukan variabel

4. String

5.

Run Module:

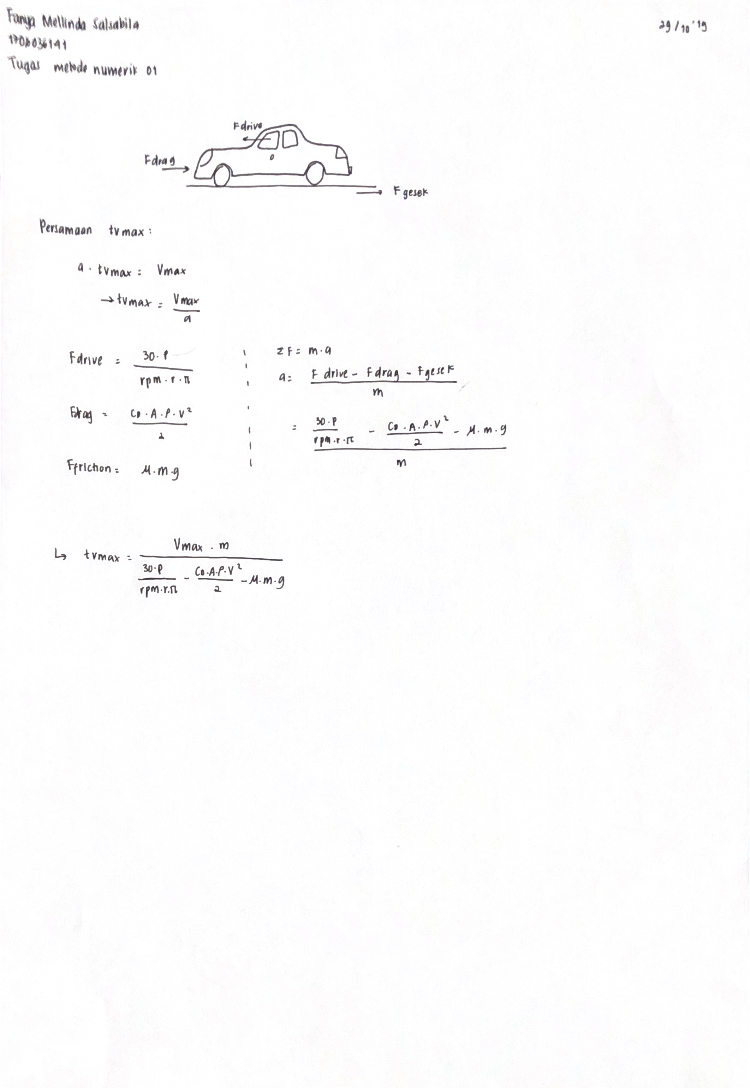
Tugas 29 Oktober 2019

Pertemuan 05 November 2019

Engineering Problems

Runge-Kutta Method

Dalam analisis numerik, metode Runge-Kutta adalah keluarga metode iteratif implisit dan eksplisit, yang mencakup rutin terkenal yang disebut Metode Euler, yang digunakan dalam diskretisasi temporal untuk solusi perkiraan persamaan diferensial biasa.

Metode Runge-Kutta merupakan alternatif lain dari metode deret taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapat derajat ketelitian yang lebih tinggi, dan sekalius menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f(x,y) pada titik terpilih dalam setiap selang langkah. Metode Runge-Kutta adalah metode PDB yang paling populer karena banyak di pakai dalam praktek.

Jenis-jenis metode Runge-Kutta:

1. Runge-Kutta orde satu

2. Runge-Kutta orde dua

3. Runge-Kutta orde 3

Metode Runge-Kutta yang terkenal dan banyak dipakai dalam praktek adalah metode Runge-Kutta orde tiga dan metode Runge-Kutta orde empat. Kedua metode tersebut terkenal karena tingkat ketelitian solusinya tinggi (dibandingkan metode Runge-Kutta orde sebelumnya, mudah diprogram, dan stabil)

4. Runge-Kutta orde 4

5. Runge-Kutta orde 5

CFDSOF-NG