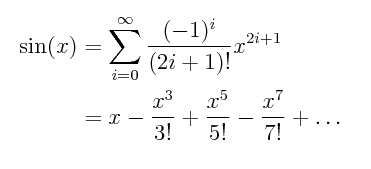Ahmad Muzakki

---

Profil

Nama  : Ahmad Muzakki

NPM  : 1706986284

Jurusan : Teknik Mesin

Pertemuan 1 (Selasa, 3 September 2019)

Pada pertemuan kali ini dibuka dengan penjelasan mengenai betapa pentingnya mata kuliah Metode Numerik yang sebelumnya kita juga sudah mempelajari Kalkulus 1, Kalkulus 2, Aljabar Linear dan Matematika Teknik, yang dimana diajarkan cara menyelesaikan suatu masalah dengan cara Eksak. Namun cara tersebut tidak cukup efektif digunakan untuk menyelesaikan permasalahan yang sangat rumit atau melibatkan suku yang jumlahnya takhingga. Metode Numerik adalah suatu operasi memformulasikan persamaan matematika. Dalam penghitungan manusia dan kalkulator sederhana memiliki keterbatasan sehingga penghitungan numerik menggunakan komputasi. Salah satu komputasi paling sederhana yaitu menggunakan Microsoft Excel. Dengan komputasi dapat melakukan penghitungan lebih efisien dan akurat. Materi pertemuan hari ini diberikan studi kasus formulasi yang digunakan untuk menghitung Deret Taylor dari Sin phi/7. Deret Taylor ini untuk mengaproksimasikan nilai fungsi dengan jumlah dari turunan yang tak terhingga. Dalam menghitung fungsi ini terdapat beberapa konstanta yaitu:

i = turunan ke-i

X = phi/7

Ratio = suku n/suku n-1 yang dimasukkan dengan rumus = -1*(Nilai X)^2/((2*Nilai i+1))

Suku = Dimasukkan dengan rumus = Suku ke-n*Rasio pada nilai i

Fungsi = Dimasukkan dengan rumus = Fungsi ke n-1 + Suku ke n

Error = Dimasukkan dengan rumus = ABS(suku ke n/fungsi ke n-1)

Berdasarkan hasil komputasi dari table diatas, maka nilai dari Sin(phi/7) = 0.43388. Hasil yang didapat dari nilai Sin(phi/7) juga ditentukan berdasarkan nilai error yang diperlukan, dalam software Microsoft Excel ini hanya dapat menggunakan maksimal 9 nilai error.

Tugas 1

Tugasnya yaitu mereview materi di pertemuan 1 dengan mencari nilai dari Cos(phi/7) dan e^(phi/7) dengan menggunakan Microsoft Excel.

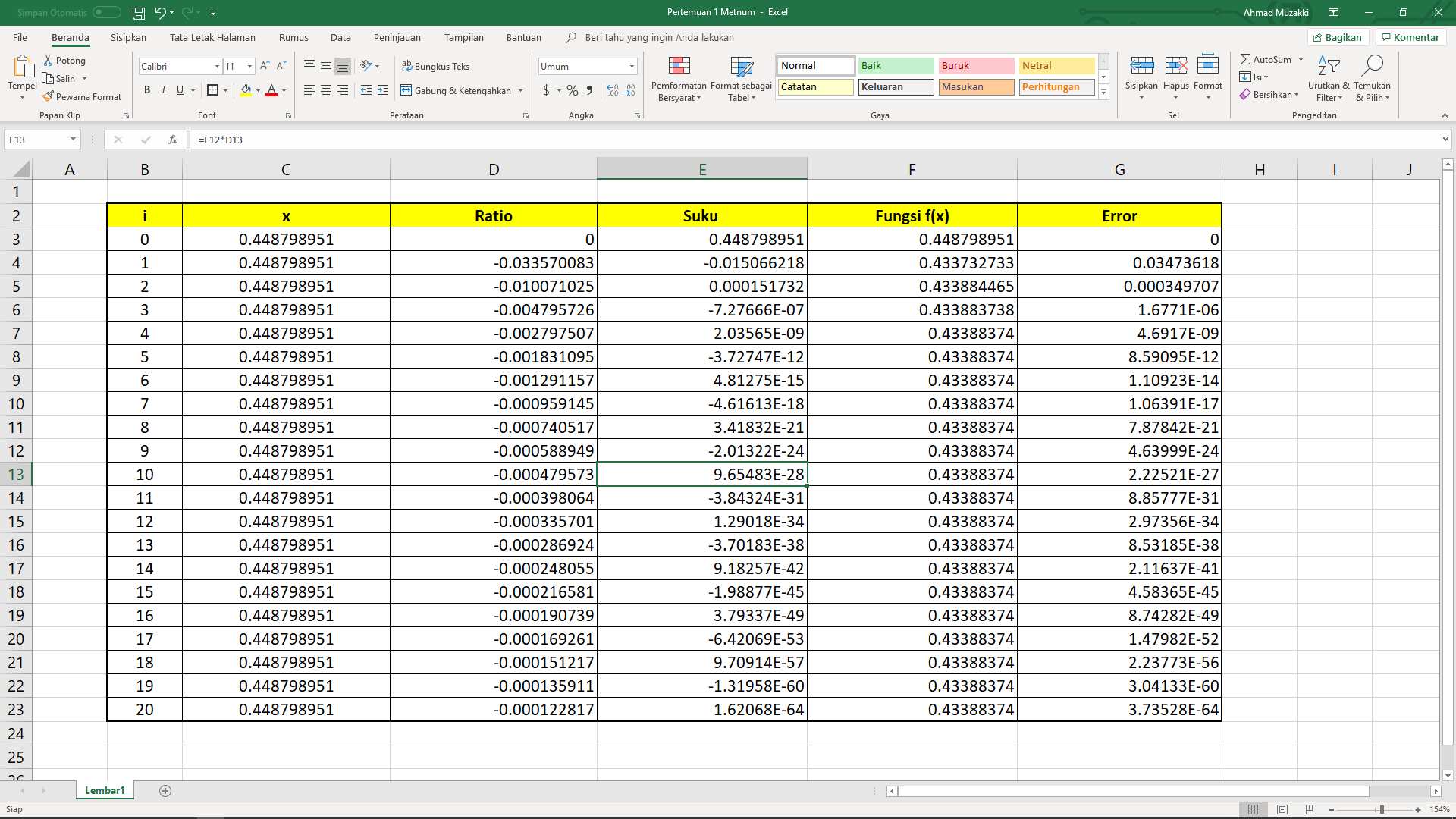
1) Akpromisasikan nilai Cos(phi/7)

Melihat dari Deret Taylor Cos(x) maka rationya = -1*(Nilai x)^2/((2*Nilai i)*(2*Nilai i-1))

Berdasarkan table tersebut maka nilai Cos(phi/7)= 0.90097

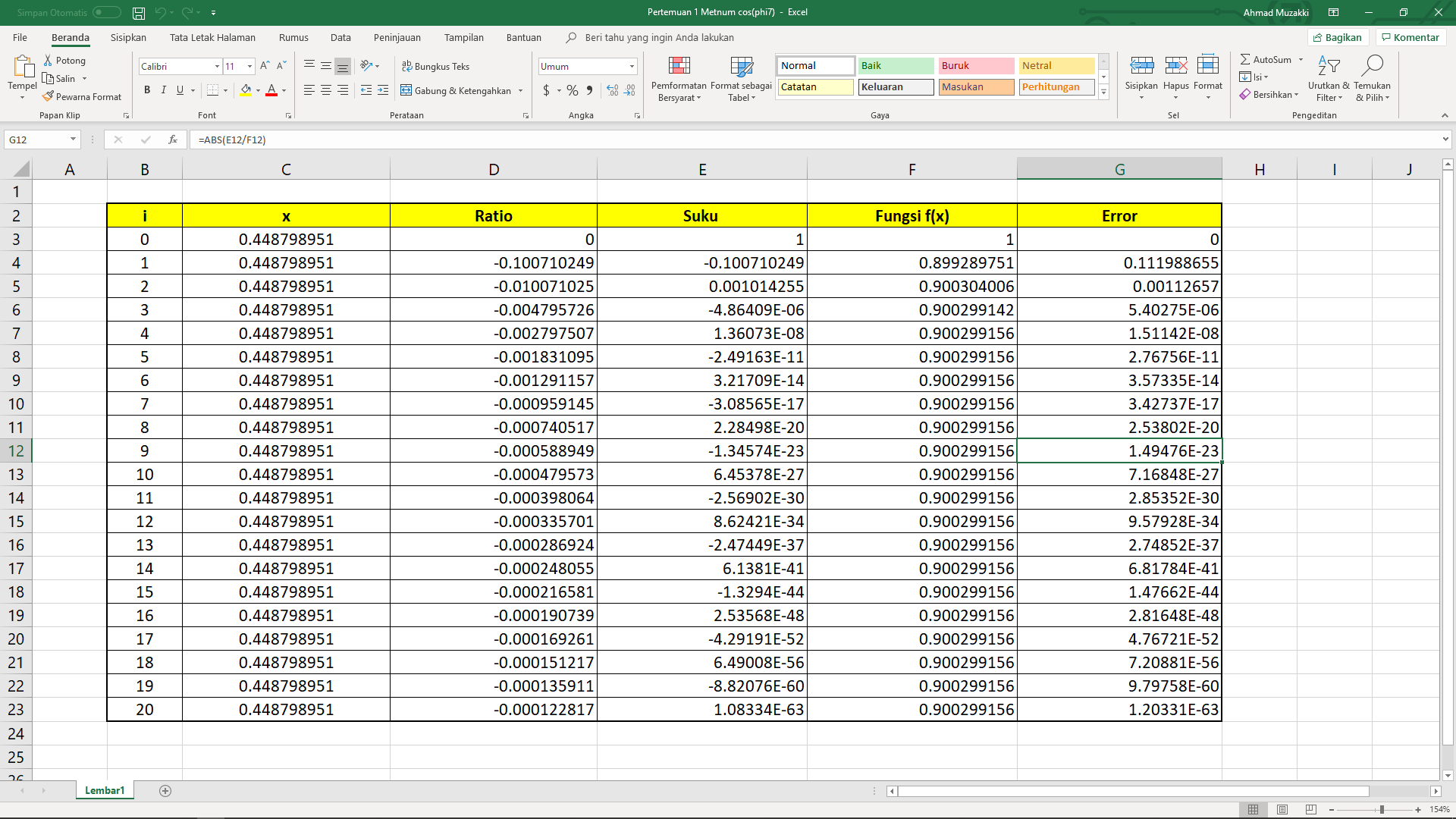
2) Akpromisasikan e^(phi/7)

Melihat dari Deret Taylor e^(phi/7) maka rationya = Nilai x/Nilai i

Berdasarkan table tersebut maka nilai e^(phi/7) = 1.5664

Pertemuan 2 (Selasa, 10 September 2019)

Pada pertemuan kedua kali ini dilanjutkan materi pembelajaran dengan hal yang tentunya sangat mendasar dalam mata kuliah Metode Numerik, yaitu Jenis-jenis Bahasa Pemrograman. Jeni-jenis bahas pemrograman sangatlah banyak, namun yang Pak Engkos sebutkan dan jelaskan hanya beberapa saja diantaranya :

- Pseudo Code

- Bahasa Pemrograman C++

- Python

- Bahasa C

- PHP

- Visual Basic

- Java

- JavaScript

Kemudian Pak Engkos memberikan contoh penerapan dari salah satunya, yaitu Pseudo Code. Berikut merupakan contoh pemrograman untuk mencari nilai dari sin(x) dengan menggunakan Pseudo Code

i=1

err=1

suku=x

sin=suku

while err>1e-7

{

ratio=-(x^2)/(2*i)/(2*i+1)

suku=suku*ratio

err=abs(suku/sin)

sin=sin+suku

i=i+1

}

Pertemuan 3 (Selasa, 17 September 2019)

Turunan numerik

Turunan numerik ialah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk table. Dalam melakukan perhitungan turunan metode numerik, intinya kita sangat dianjurkan untuk menggunakan alat hitung baik kalkulator maupun komputer. Kenapa ?, karena kita akan berurusan dengan angka yang memiliki banyak koma. Kemudian kita juga mendapat data-data berupa nilai-nilai suatu titik (nilai x dan y(f(x)). Kemudian kita akan mengidentifikasi metode yang akan kita gunakan berdasarakan data yang ada atau nilai yang akan kita cari.

Metode yang kita gunakan ada 3, yaitu turunan maju, turunan mundur, dan turunan pusat. Tetapi rumus yang digunakan berbeda untuk rumus turunan ke-1 dan ke-2. Perlu diingatkan juga bahwa jarak antar titik yang akan digunakan dalam perhitungan haruslah sama.

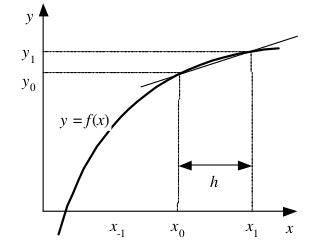
Turunan Maju (Forward)

f’(x0) = f(x1)-f(x0)/(x1-x0)

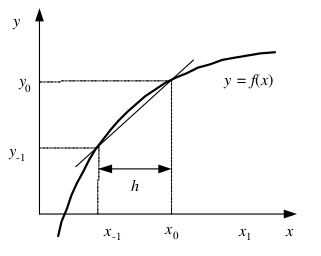
Turunan Mundur (Backward)

f’(x0) = f(x0)-f(x-1)/(x0-x-1)

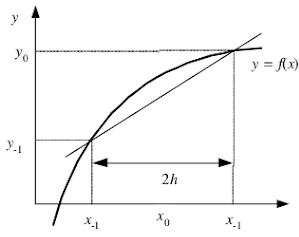
Turunan Pusat (Center)

f’(x0) = f(x+1)-f(x-1)/(x+1-x-1)

Untuk nilai h yang sama mengunakan metode Center sangatlah dianjurkan karena mempunyai tingkat keakuratan yang paling baik. Namun terlepas dari metode yang digunakan untuk mendapatkan nilai dengan keakuratan terbaik bisa didapatkan dengan memasukan nilai h sekecil mungkin.

Kuliah Metode Numerik, 24 September 2019

Kuliah dimulai dengan review singkat mengenai energi dan termodinamika. Hal-hal yang di review antara lain:

Formula energi bebas Gibbs

Energi dalam, energi yang ada pada suatu benda karena gerak molekulnya

Energi potensial, di mana setiap benda atau energi berusaha mencari potensial terendahnya

Gerak molekul, di mana molekul bergerak secara translasi, rotasi, dan vibrasi.

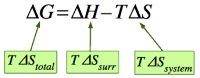
Energi Gibbs, entalpi dari sebuah sistem dikurangi temperatur dikalikan entropi sistem. Persamaan enegi bebas Gibbs dibuat untuk mempermudah agar tidak lagi diperlukan tabel dan tidak perlu menggunakan interpolasi yang rumit

Kuliah Metode Numerik, 1 Oktober 2019

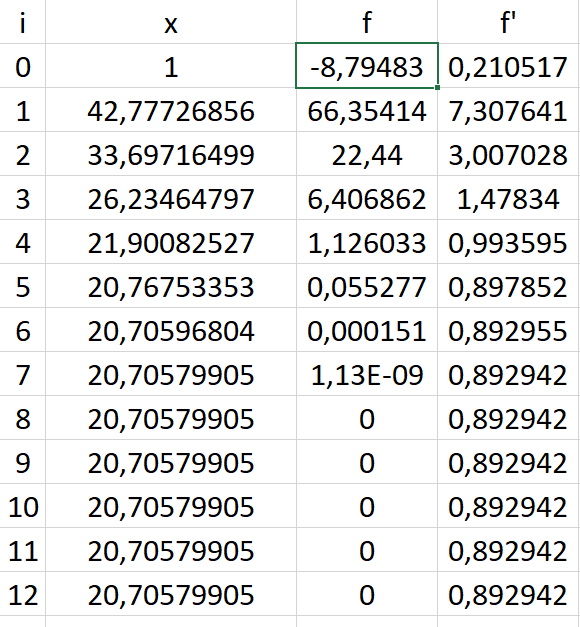
Pada permulaan kelas, dicoba untuk menyelesaikan persamaan fungsi f(x)=exp(0,1x)+0,1x-10 menggunakan program Excel. Pada program, dimasukkan tiga kolom, kolom x, f(x), dan f'(x).

f'(x) dari f(x) adalah 0,1*exp(0,1x)+0,1

Dalam program Excel, dapat ditulis sebagai berikut

Truncation Error

Truncation Error terjadi ketika kita memotong deret taylor agar membuatnya menjadi terhingga. Sederhananya, error tersebut adalah error yang terjadi ketika ada perbedaan antara jumlah yang terpotong dengan jumlah yang sebenarnya.

Jika kecenderungan numerik sudah terasa logis dan sama dengan eksperimen, maka numerik bisa dianggap layak digunakan. Jika tidak, maka metode numerik belum layak untuk digunakan sebagai cara validasi eksperimen.

Kuliah Metode Numerik, 29 Oktober 2019

Pertemuan hari ini yaitu membahas tentang Bahasa pemrograman (Phyton),yang dimana bahasa yang digunakan bisa dianggap relatif lebih sederhana daripada C++ karena yang harus dideklarasikan lebih sedikit. Diajarkan jikalau Phyton pada umumnya ditulis menggunakan perangkat lunak Phyton DLB. Pada perangkat lunak Phyton DLB, pertama diajarkan untuk memasukkan kode berikut: import math math.sqrt (x) perintah import math diatas membuat Phyton DLB memuat fungsi matematika, sedangkan perintah math.sqrt (x) adalah perintah akar kuadrat, dan x adalah angka yang dikehendaki dicari akarnya. Perintah math.sqrt juga bisa diganti menjadi perintah lain, yaitu dengan memasukkan kata perintah yang dikehendaki diikuti sama dengan math.sqrt, contohnya: akar = math.sqrt Kemudian, mahasiswa diminta untuk menuliskan perintah deklarasi suatu kata sama dengan suatu angka, contohnya: x = 30 y = 20 z = 10 Diajarkan pula perintah pow atau power, dimana pow adalah perintah untuk memangkatkan. Sebagai contoh, perintah pow (x,y) berarti memerintahkan sistem untuk memangkatkan angka 30 sebanyak 20 kali. Terakhir diajarkan fungsi string, dimana string adalah fungsi untuk mendeklarasikan suatu kalimat. Contoh lengkap kode Phyton yang digunakan pada hari ini adalah sebagai berikut: