Latitia Dhayita Pramudito
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Nama : Latitia Dhayita Pramudito
NPM : 1706986385
Mahasiswa Departemen Teknik Mesin 2017
Contents
Pertemuan Pertama Metode Numerik
Hari, Tanggal : Rabu, 4 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pada pertemuan pertama, Pak Dr. Ahmad Indra atau yang biasa disapa Pak Dai menjelaskan setiap pelajaran yang kita ambil, harus kita serap ilmunya. Lalu Pak Dai memberikan contoh berupa pertanyaan, mengapa kita perlu belajar mata kuliah Kalkulus? Alasan dibalik itu karena dalam mata kuliah Kalkulus kita dapat mengambil ilmu-ilmu dan logika matematika yang nantinya akan digunakan untuk mata kuliah mesin kedepannya. Seperti mata kuliah matematika teknik, termodinamika, heat transfer, dll
Metode Numerik merupakan bagian dari ilmu matematika yang cara penyelesaiannya menggunakan metode numerik. Bahasa pemograman yang digunakan adalah Python. Metode numerik digunakan untuk mengerjakan persoalan matematika yang rumit menjadi lebih sederhana. Namun, biarpun metode numerik dijadikan solver, ide tetap berasal dari manusia.
Untuk menunjang ide-ide tersebut digunakan langkah-langkah. Langkah-langkah berupa instruksi yang dibutuhkan untuk komputer. Karena itulah diperlukan bahasa penulisan dari bahasa natural yang kita mengerti dirubah menjadi bahasa mesin atau yang biasa disebut bahasa pemograman. Jadi, langkah-langkah yang kita buat akan menggunakan bahasa pemograman. Untuk membantu membuat bahasa pemograman dapat digunakan flow chart. Flow chart merupakan instruksi yang menggunakan bagan dengan simbol-simbol tertentu.
Selain itu, dalam mata kuliah ini yang dinilai adalah gradien dari hasil mahasiswa. Dicontohkan dengan sebuah grafik dengan sumbu y : Lesson Learn dan sumbu x : Waktu (6 bulan). Jadi yang dilihat adalah proses dari awal mahasiswa mengikuti kelas metode numerik sampai selesai selama 6 bulan berlangsung.
Lalu pak Dr. Eng. Radon Dhelika atau yang biasa disapa Pak Radon juga menambahkan, bahwa skill pemograman sangat dibutuhkan di pasar industry 4.0 sekarang. Jadi, sebagai mahasiswa Teknik Mesin UI harus menyerap ilmu sebanyak-banyaknya dan tidak menyianyiakan mata kuliah ini karena mata kuliah metode numerik merupakan mata kuliah wajib yang disediakan yang banyak mempelajari bahasa pemograman. Selain itu, alasan penggunaan bahasa Python di departemen teknik mesin UI adalah berkaca dari Massachusetts Institute of Technology (MIT) yang menerapkan Python pada mahasiswa teknik mesin nya untuk pembelajaran bahasa pemograman.
Pada akhir pertemuan, diberikan tugas untuk : 1. Belajar langsung menggunakan Python masing-masing 2. Membuat program utuk menyelesaikan persoalan T(x)= (x^2-1)/(x-1) dalam bentuk algoritma / flowchart
Setelah melakukan beberapa kali percobaan dan mencari-cari info dari berbagai sumber seperti buku dan internet, saya berhasil mendapatkan algoritma untuk persoalan T(x)= (x^2-1)/(x-1).
Algoritma yang saya gunakan menggunakan modul sympy
from sympy import *
x= symbols('x')
hasil = limit(((x ** 2) - 1 )/ (x - 1), x, 1)
print(hasil)
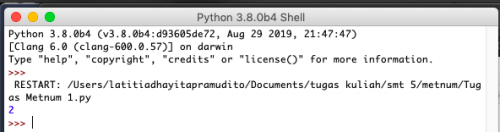
Hasil yang didapatkan setelah melakukan run pada algoritma diatas adalah :
2
Pertemuan Kedua Metode Numerik
Hari, Tanggal : Rabu, 11 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Artificial Intelligence (AI)
Rekayasa Kecerdasan. Berguna untuk membantu manusia dan dibuat seakan menyerupai manusia. Tetapi yang mmiliki kecerdasan sebenarnya adalah manusia. Tetapi manusia memiliki keterbatasan. Namun dibalik keterbatasannya, manusia memiliki hal yang tidak dimiliki robot buatan yaitu Hati
Menurut pak Dai, Industry 5.0 adalah PancasilaKarena teknologi harusnya dikuasai oleh manusia jadi jangan sampai teknologi melemahkan manusia. Manusia tidak boleh di drive oleh teknologi. Namun, manusia yang mendrive teknologi dengan cara mengerti teknologi itu sendiri. Contoh, mahasiswa teknik mesin maka bisa dengan belajar metode numerik.
Belajar metode numerik membuat kita berhubungan dekat dengan komputer. Komputer dapat membantu kita dalam berbagai hal salah satunya adalah menghafal berbagai angka. Contoh dalam permainan catur melawan komputer, komputer didalamnya sudah menyimpann database untuk mengingat gerakan-gerakan untuk melawan kita. Karena itu, sebagai partner kita, kita harus mengenal komputer mulai dari istilah-istilah yang digunakan. Istilah salah satunya adalah 32 bit dan 64 bit.
Perbedaan 32 bit dan 64 bit :
Sistem operasi 32 bit hanya mampu menggunakan RAM berkapasitas maksimal 4 GB sedangkan batas maksimal RAM yang mampu dibaca sistem operasi 64 bit adalah 192 GB. Selain itu, sistem operasi 32 bit hanya mampu memproses data sebesar 64 nilai komputasi sedangkan sistem operasi 64 bit mampu memproses data hingga 256 nilai komputasi dalam sekali siklus pemrosesan.
Seperti dalam otak manusia, manusia mampu menyimpan data dalam binary digit. Jika 64 bit, maka komputer memiliki kemampuan yang lebih akurat dan cepat. Karena itu, sekarang hampir semua gadget yang digunakan menggunakan sistem 64 bit.
Untuk memperkaya wawasan kita akan metode numerik, kita dapat bereksekusi langsung dengan belajar Python. Berbagai situs sudah dirancang untuk mempermudah manusia belajar Python. Salah satunya adalah [1] Selain itu, jika kita kesulitan dalam penginstallan python pada laptop atau komputer, kita dapat menggunakan situs [2] untuk mengakses Python tanpa menginstall Python.
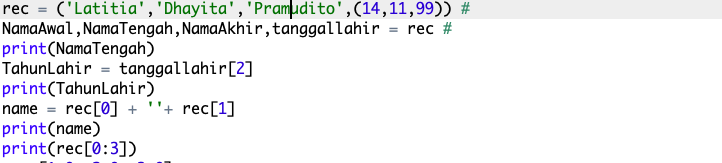
Pada pertemuan kali ini, mahasiswa diminta untuk berlatih dalam penggunaan tuples & lists di Python. Dan ini hasil pengerjaan saya :
Pertemuan Ketiga Metode Numerik
Hari, Tanggal : Rabu, 18 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
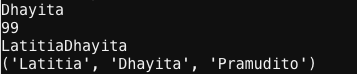
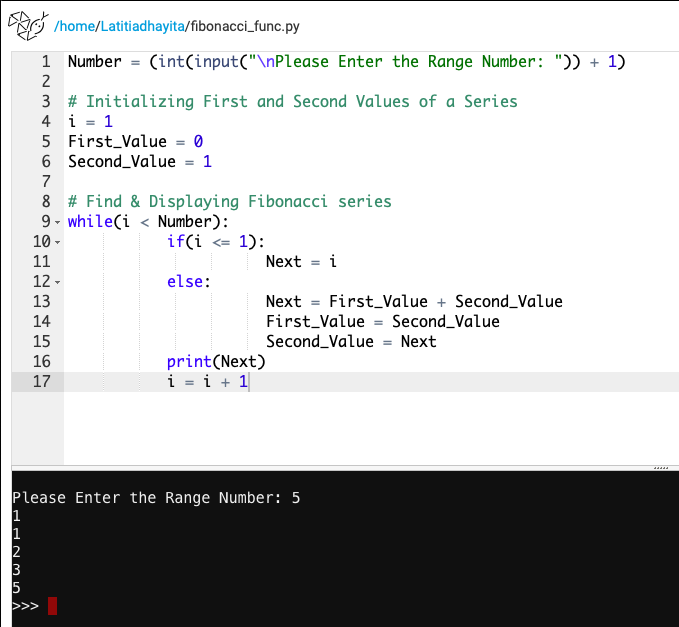
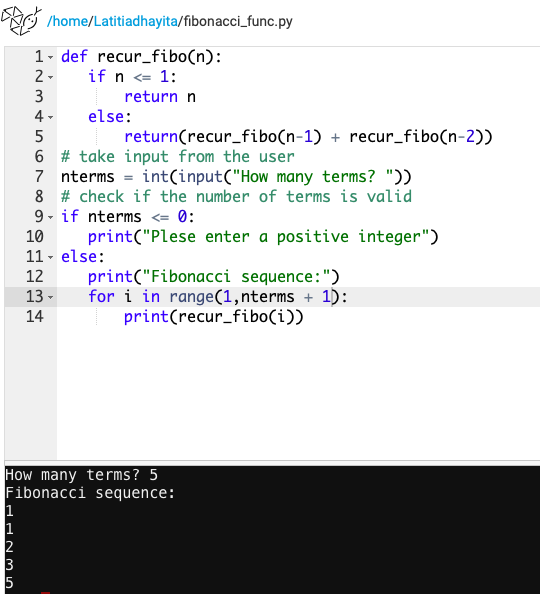
Pada pertemuan ini diadakan kuis tentang dasar-dasar bahasa python. Kuis yang diberikan berisikan tentang Fibonacci Sequence. Hasil dari jawaban saya adalah berikut dibawah ini :
Metode yang saya gunakan diatas adalah dengan menggunakan Loop dengan while condition.
Selain itu, pada metode ini saya menggunakan function.
Pertemuan Keempat Metode Numerik
Hari, Tanggal : Rabu, 25 September 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Pelajaran hari ini, mempelajari apa itu Pemodelan Komputer. Dalam mempelajari sebuah konsep lebih baik mengerti apa isi dari konsep tersebut. Karena itu hari ini kita belajar terlebih dahulu isi dari pemodelan komputer.
Numerical Computing -> Pemodelan Komputer
Pemodelan Komputer terdiri dari modelling dan computation.
Sebelumnya, mengapa kita harus berhitung? (Dalam ranah teknik)
Karena apa yang telah di design hasilnya harus dipastikan berfungsi secara baik, reliable dan berfungsi secara optimal. Namun manusia memiliki keterbatasan, tetapi bisa menghitung secara pendekatan. Contoh untuk menghitung 0/0 hasilnya bukan tidak ada namun kita tidak tahu tetapi bisa dilakukan melakukan pendekatan. Untuk itu sebagai manusia kita harus memiliki value dalam diri kita seperti komputer jika listrik mati tidak akan bisa menyimpan lagi. Sama seperti value dalam diri kita.
Selanjutnya kita belajar apa itu model?
Model adalah sebuah representasi yang di asumsikan agar dapat mensimplifikasi dari keadaan real yang rumit menjadi lebih simple.
Jadi model terdiri dari 3 unsur yaitu :
1. Representasi
2. Simplifikasi
3. Asumsi
Contoh dari sebuah model pada fondasi. Untuk menghitung kekuatan fondasi menahan beban. Fondasi di modelkan dalam bentuk 2D dan di asumsikan Modulus Elastisitas pada semua titik sama, lalu mensimplifikasi dengan menggunakan model 2D.
Dari berbagai model yang kita buat, dibutuhkan ilmu dalam membangun persamaan aljabar dan memodelkan persamaan dalam komputasi. Untuk itu kita harus belajar giat serta berlatih sejak dini untuk menggunakan komputasi. Selain itu ada juga aplikasi dari komputasi yaitu Diskritisasi yaitu membuat sesuatu yang kontinu menjadi titik-titik yang berhingga.
Pertemuan Kelima Metode Numerik
Hari, Tanggal : Rabu, 2 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Semua masalah yang didapat dapat dimodelkan, model dapat memudahkan dalam penyelesaian masalah. Salah satunya dengan menggunakan Bahasa Python sebagai penyelesaian masalah. Menagapa bahasa Python?
Karena Python merupakan bahasa yang GRATIS dan semua orang saat ini sedang gunakan dalam Industry 4.0
Pada pertemuan ini mempelajari :
-Aplikasi Aljabar yang akan dimodelkan pada Sistem Pegas
Tugas untuk minggu depan adalah :
- Membaca Metode Runge-Kutta
Pada pertemuan kali ini, Asisten Dosen menjelaskan tentang Penggunaan Pemodelan pada Sistem Tunggal menjadi sebuah persamaan linier dengan menerjemahkan rumus yang biasa digunakan pada materi Pegas menjadi sebuah Matrix.
Selain itu pada pertemuan ini mempelajari tentang Cara Pembuatan Matrix Pegas yang bukan Tunggal yaitu dengan menerapkan Superposisi Matrix. Lalu, diberikan contoh pemodelan sistem ganda pada pegas seri.
Terakhir diberikan penjelasan dan cara penggunaan modul yang dapat digunakan pada Python yang dapat memudahkan perhitungan Sistem Persamaan Linier yaitu :
- Numpy
- Sympy
Pertemuan Keenam Metode Numerik
Hari, Tanggal : Rabu, 9 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Kemarin belajar memecahkan satu set persamaan aljabar. Satu set bisa 100,1000,100000 persamaan aljabar.
Langkah2 teknik menyelesaikan aljabar :
- metode eliminasi : mengurangi variable dr persamaan berikutnya, sehingga persamaan akhirnya hanya 1 variable lalu nanti disubstitusi.
- Gauss
- Trial and Error dll
Yang perlu diketahui adalah peran komputer dalam permodelan. Logika tetap dari human namun komputer membantu mempercepat perhitungan.
Karena itu kemarin kita berdiskusi tentang sebuah permodelan dari suatu permasalahan menjadi persamaan aljabar.
Kontinu Assumption :
- contoh dalam satu ruangan dipenuhi oleh oksigen, maka tidak ada ruang hampa dalam ruangan. Seluruh ruangan dipenuhi oleh oksigen dan kita dapat mengukur Temperature dititik manapun dalam ruangan
- contoh lagi pada meja, dianggap seluruh meja memiliki massa. Saat diduduki atau diberikan external force maka seluruh titik akan merasakan external force.
Formasi dan udara mungkin tidak terlihat tetapi harus kita bayangkan. Karena imajinasi lebih powerful dari knowledge.
Model matematis nanti akan berupa persamaan diferensial. Adanya persamaan diferensial karena permasalahan yang kita hadapi terjadi secara kontinu. Kontinu Assumption jika diberikan gaya maka setiap titik akan merasakan beban maka setiap titik akan berdislokasi atau berpindah tempat. selisih perpindahan tempatnya disebut dengan displacement (u). Perubahan displacement disebut (du) artinya limit ketika delta u menuju 0 tetapi tidak 0. Jadi diferensial itu sangat kecil namun tidak 0
Pembicaraan ini dilakukan untuk menjadi mahasiswa cerdas bukan hanya pintar. Cerdas yang dimaksud adalah berpikir kedepannya. Mata kuliah metode numerik lebih cocok dengan mata kuliah Computer Aided Engineering
HASIL QUIZ 2
Hari, Tanggal : Rabu, 16 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Hasil Pemograman saya untuk Problems 2.1 nomor 6 dibawah ini :
from numpy import linalg
import numpy as np
row1 = [0,0,2,1,2]
row2 = [0,1,0,2,-1]
row3 = [1,2,0,-2,1]
row4 = [0,0,0,-1,1]
row5 = [0,1,-1,1,-1]
v = np.array ([1,1,-4,-2,-1])
print ("berikut adalah matriks dari Y: ")
print (v)
c = np.array ([row1,row2,row3,row4,row5])
print ("berikut adalah nilai n pada matriks : ")
print (c)
hasil = linalg.solve (c,v)
p = int(hasil[0])
q = int(hasil[1])
r = int(hasil[2])
s = int(hasil[3])
t = int(hasil[4])
print ("nilai dari x = ")
print ("x1= ",p)
print ("x2= ",q)
print ("x3= ",r)
print ("x4= ",s)Insert non-formatted text here
print ("x5= ",t)
Hasil Pemograman saya untuk Problems 7.1 nomor 2 dibawah ini
# nilai y dicari dari x yang diketahui
# menggunakan step size L # nilai awal b saat a
def dydx(x, y):
return ((x**2 - 4*y))
def rungeKutta(a, b, x, L):
# menghitung n iterasi dengan step size L
n = (int)((x - a)/L)
y = b
for i in range(1, n + 1):
"untuk mencari y menggunakan metode Runge-Kutta"
k1 = L * dydx(a, y)
k2 = L * dydx(a + 0.5 * L, y + 0.5 * k1)
k3 = L * dydx(a + 0.5 * L, y + 0.5 * k2)
k4 = L * dydx(a + L, y + k3)
# nilai selanjutnya pada X
a = a + L
# nilai selanjutnya pada Y
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
return y
#memasukan nilai (a,y,x,L) sesuai dengan soal :
a = 0
y = 1
x = 0.03
L = 0.01
print ('nilai y pada x:', rungeKutta(a, y, x, L))
Hasil Jawaban UTS Metode Numerik
Hasil Pemograman Soal A
from math import *
g = 9.81
- besar massa asumsi
m1 = eval(input("Massa 1: "))
m2 = eval(input("Massa 2: "))
m3 = eval(input("Massa 3: "))
- besar kemiringan
sudut = eval(input("Sudut Kemiringan: "))
- besar percepatan
a = eval(input("Acceleration: "))
- besar koefisien gesek
myu1 = eval(input("Koef. Gesek1: "))
myu2 = eval(input("Koef. Gesek2:"))
myu3 = eval(input("Koef. Gesek3: "))
x = sin(sudut)
y = cos(sudut)
- perhitungan tegangan tali 1,2,3
T1 = m1*g*(x-myu1*y) - m1*a
T2 =m2*g*(x-myu2*y) + T1 - m2*a
T3 =m3*g*(x-myu3*y) + T2 - m3*a
print ("Besar Tegangan Tali 1: ",T1)
print ("Besar Tegangan Tali 2: ",T2)
print ("Besar Tegangan Tali 3: ",T3)
Hasil Pemograman Soal B
from math import *
from sympy import *
dens = 1.2
g = 9.81
m = eval(input("massa mobil terkena angin (kg): "))
cd = eval(input("drag coefficient: "))
vtop = eval(input("top speed (m/s): "))
luas = eval(input("luas (m2): "))
a = eval(input("acceleration (m/s<2):"))
myu = eval(input("koefisien gesekan: "))
f1 = a
fs = g*myu
for v0 in range (0,vtop) :
#perhitungan gesekan ban dan hambatan aerodinamis
fdrag=(cd*v0**3/2)/m
atot = f1 - (fdrag + fs)
t = -(vtop)/atot
print ("total acceleration (m/s~2):",atot)
print ("waktu yang dibutuhkan sampai kecepatan top speed: ",t)
- semua dibagi m
VIDEO PENJELASAN HASIL UTS
Terima Kasih telah membaca blog Wiki saya, apabila ada yang ingin disampaikan dapat mengisi kolom komentar dibawah ini.




Enable comment auto-refresher