Aulia Rifai
Mengapa mahasiswa Teknik Mesin perlu mempelajari Kalkulus? Kuliah 1 (4 September 2019)
Kalkulus merupakan alat penyelesaian masalah yang membantu logika berpikir serta aturan dalam penghitungan yang bersifat matematis.
Tugas 1 Metode Numerikal
Menyelesaikan lim (x^2-1)/(x-1) menggunakan Phyton. Dalam mengerjakan menggunakan Phyton saya mempelajari bahwa mengunakan limit ternyata sedikit sulit serta mempelajari Bahasa baru yaitu 'def' , 'print' , 'if' , serta 'else'. dalam mengerjakan soal ini langkahnya adalah,
1. Saya memfaktorkan (x^2-1) menjadi (x+1) dan (x-1) kemudian dibagi (x-1) menghasilkan (x+1)
2. Saya menentukan bahwa limit mendekati 1 adalah untuk persamaan (x+1)
3. Menggunakan Jupyter saya mulai menuliskan coding untuk penghitungan limit
4. Kemudian hasil keluar, dapat dilihat bahwa limit kiri mendekati limit kanan sehingga hasil limit bisa dikatakan kontinu
Kuliah pertemuan kedua (11 September 2019)
Metode numeric merupakan sebuah metode untuk menyelesaikan persoalan. Menggunakan software untuk menyelesaikan metode numerical memakan sedikit waktu dikarenakan kurangnya pengalaman dan waktu dalam menggunakan program Phyton. Phyton bisa disebut juga high level language, program ini digunakan untuk menyelesaikan persamaan numeric yang sangat banyak serta mempersingkat waktu dalam mengerjakannya. Meskipun latar belakang pendidikan adalah jurusan Teknik Mesin, mempelajari Phyton dibutuhkan untuk mempermudah proses pengerjaan dan tuntutan pekerjaan yang semakin menghilangkan kotak-kotak jurusan dan menuju ke ilmu pengetahuan terapan dari berbagai fakultas dan jurusan.
Software bisa melebihi manusia dalam kapasitas analisis. Contoh penggunaan adalah saat menggunakan software untuk menjalankan uji material. Bedanya 32 bit dan 64 bit ada di kecepatan pembacaan integer, 32 bit memiliki lebih banyak limitasi dalam kecepatan pembacaan dibandingkan 64 bit. Sehingga sekarang 32 bit sudah mulai ditinggalkan dan beralih ke 64 karena lebih cepat dan lebih efisien.
Manusia semakin banyak pengetahuan seharusnya semakin berpikir menggunakan hati. Karena otaknya sudah penuh sehingga harus berpikir dibantu dengan hati atau perasaan. Semakin kita pintar seharusnya semakin merasa rendah hati dan berpikir bahwa masih banyak yang masih tidak diketahui diluar sana. Sebaliknya, semakin sedikit pengetahuan orang lain maka akan semakin merasa tinggi hati dan sombong dikarenakan ia berpikir sudah mengetahui semuanya dan merasa paling benar sendiri. Menurut Pak Dai, Industry 5.0 adalah pancasila dikarenakan seharusnya semakin tinggi sebuah teknologi bisa empowering atau menggerakan hati seseorang.
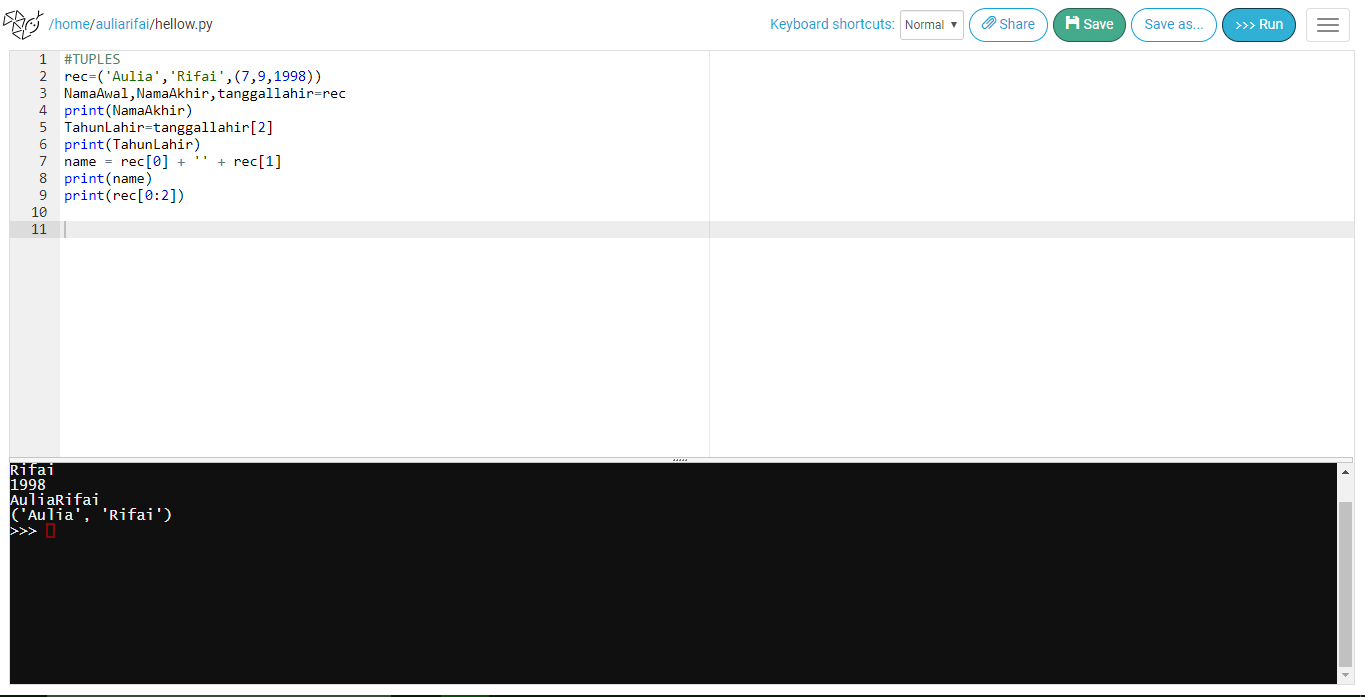
TUPLES
rec=('Aulia','Rifai',(7,9,1998))
NamaAwal,NamaAkhir,tanggallahir=rec
print(NamaAkhir)
TahunLahir=tanggallahir[2]
print(TahunLahir)
name = rec[0] + + rec[1]
print(name)
print(rec[0:2])
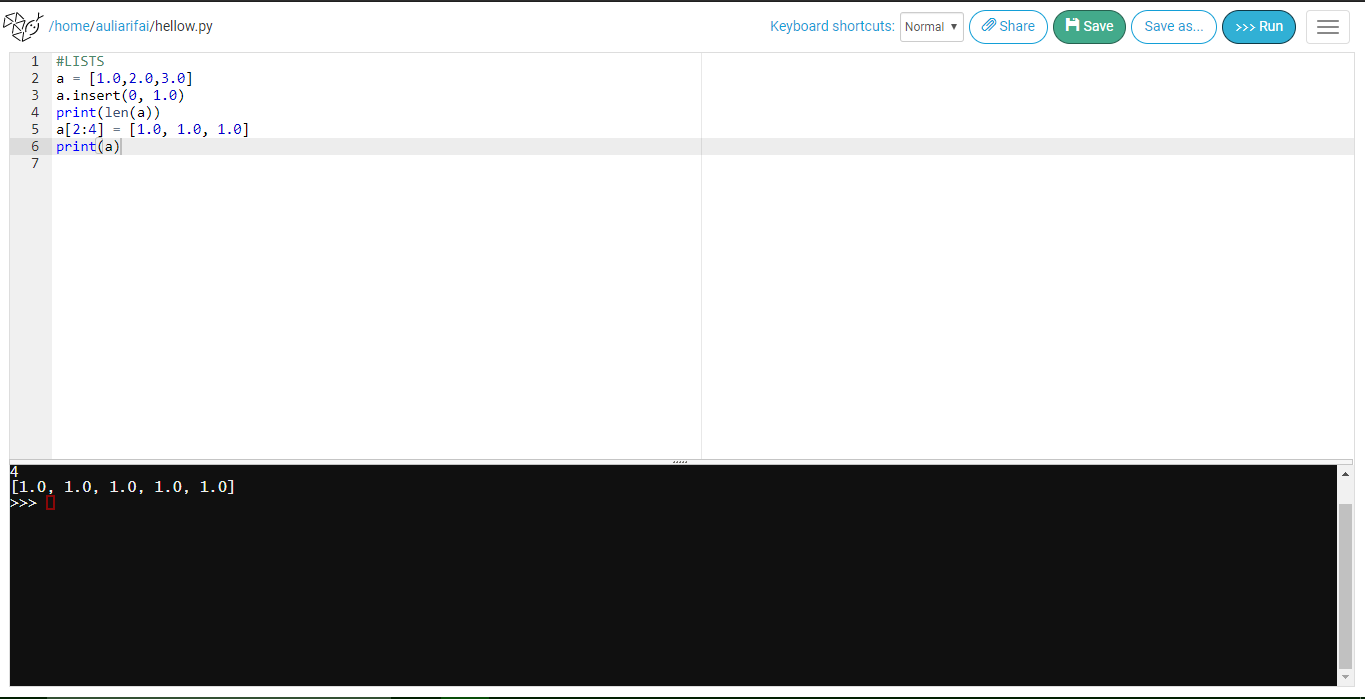
LISTS
a = [1.0,2.0,3.0]
a.insert(0, 1.0)
print(len(a))
a[2:4] = [1.0, 1.0, 1.0]
print(a)
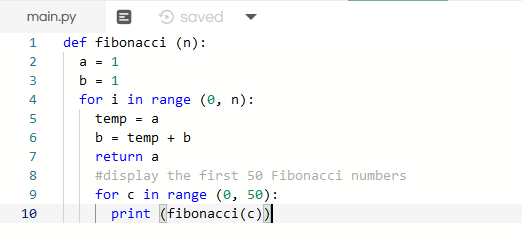
Bilangan Fibonacci
Dalam latihan kali ini, menggunakan Phyton dengan 2 metode, yaitu
1. Metode Loop
2. Metode Function
"QUIZ METODE NUMERIKAL"
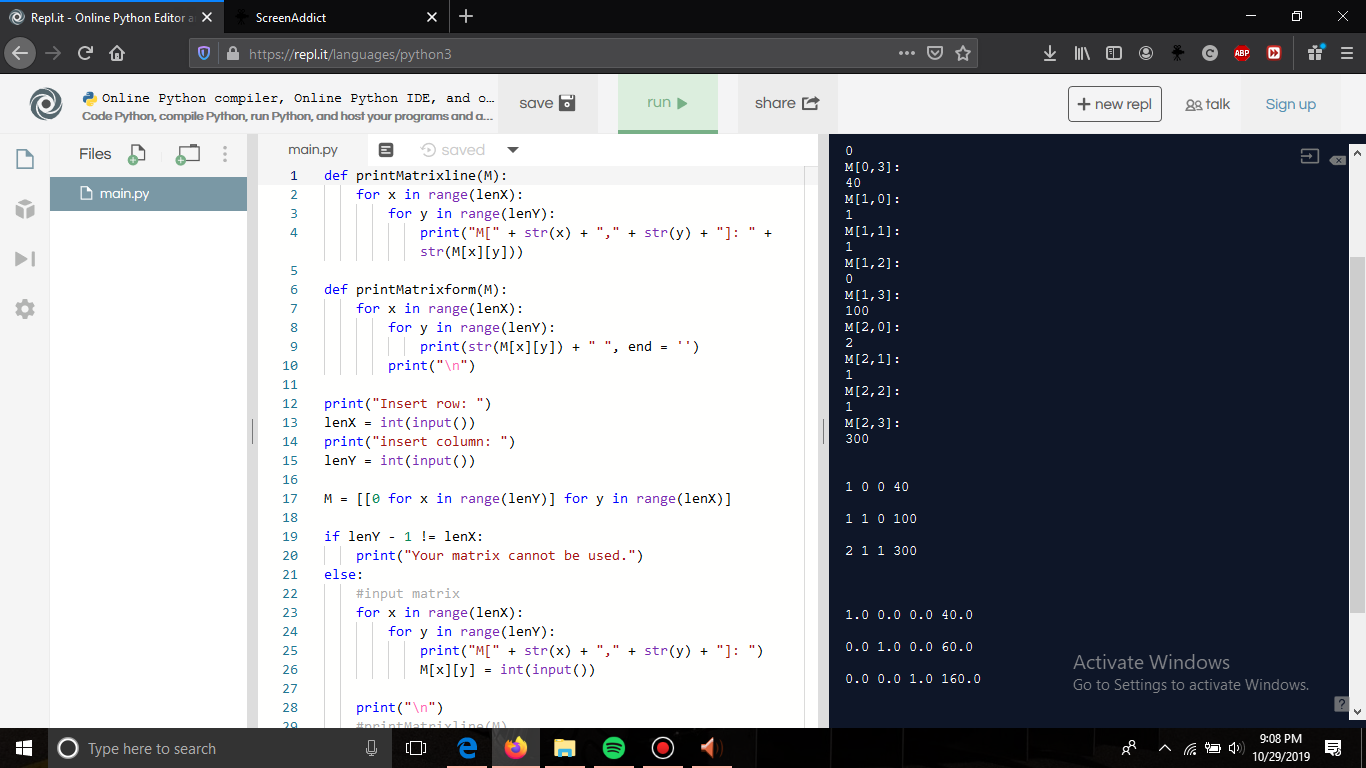
1. Solusi problem 2.1. no 6 Halaman 55 codingnya adalah sebagai berikut def printMatrixline(M):
for x in range(lenX):
for y in range(lenY):
print("M[" + str(x) + "," + str(y) + "]: " + str(M[x][y]))
def printMatrixform(M):
for x in range(lenX):
for y in range(lenY):
print(str(M[x][y]) + " ", end = )
print("\n")
print("Masukan column: ") lenY = int(input()) print("Masukan row: ") lenX = int(input())
M = [[0 for x in range(lenY)] for y in range(lenX)]
if lenY - 1 != lenX:
print("Matrix tidak bisa digunakan")
else:
#input matrix
for x in range(lenX):
for y in range(lenY):
print("M[" + str(x) + "," + str(y) + "]: ")
M[x][y] = int(input())
print("\n")
#printMatrixline(M)
printMatrixform(M)
print("\n")
flag = 0 n = lenX
for i in range(n):
if M[i][i] == 0:
c = 1
while M[i + c][i] == 0 and (i + c) < n:
c += 1
if (i + c) == n:
flag = 1
break
j = i
for k in range(n + 1):
temp = M[j][k]
M[j][k] = M[j + c][k]
M[j + c][k] = temp
for j in range(n):
if i != j:
p = M[j][i] / M[i][i]
for k in range(n + 1):
M[j][k] = M[j][k] - (M[i][k]) * p
printMatrixform(M)
for i in range(n):
if M[i][i] != 1:
p = M[i][i]
M[i][n] = M[i][n] / p
M[i][i] = M[i][i] / p
print("\n")
printMatrixform(M)
2. Problem set 7.11 No 2 Hal 263
"UJIAN TENGAH SEMESTER METODE NUMERIKAL"
Nomor 3a. Hasil coding belum selesai sejauh ini, baru memasukan rumus tegangan tali yaitu T = (1/4).(W4+m1gsina+m2gsina+m3gsina). Kemudian rencananya akan dibuat program yang menggunakan Gauss Elimination untuk menemukan tegangan tali tersebut, sejauh ini program belum dapat digunakan.
CODING GAUSS ELIMINATION
Nomor 3b
Hasil coding belum dapat diselesaikan karena masih mengerjakan logaritma pengerjaan serta menentukan runge khutta. Setelah ini akan dicari rumus penyelesaian dan coding
CODING MOBIL