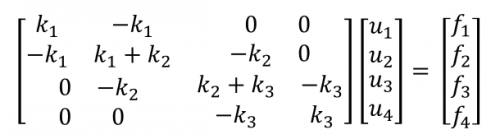Kelompok 12

Perkenalkan, kami kelompok 12 dengan anggota kelompok sebagai berikut:

1. Elvin

2. Khairun Naziri Batubara

3. Adam Ilham Maulana

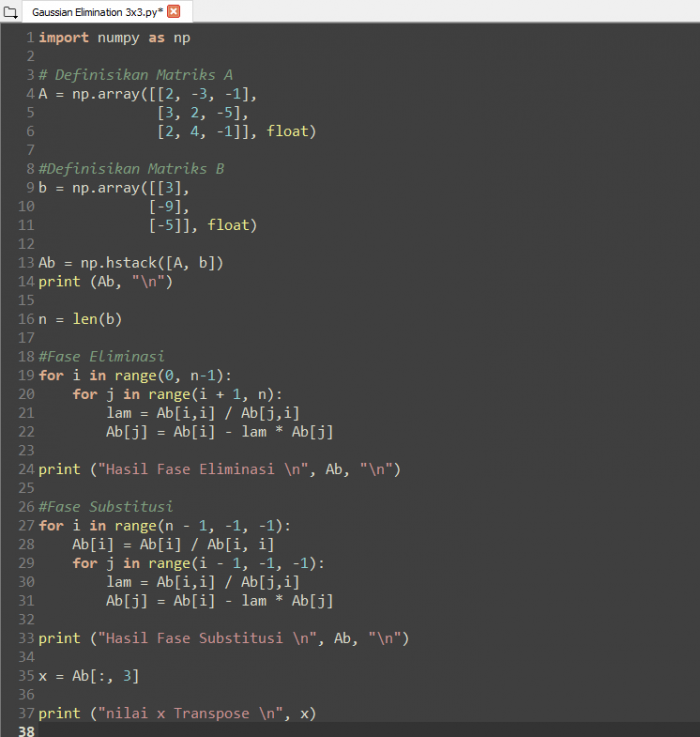
Tugas Metode Eliminasi Gauss

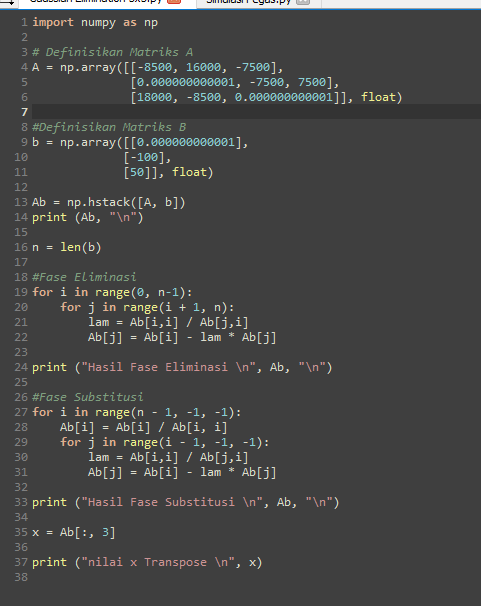
Video diatas merupakan penjelasan program eliminasi Gauss yang dibuat pada python. Rangkaian kode dari video diatas ditampilkan sebagai berikut:

Tugas Finite Element Analysis dengan Eliminasi Gauss

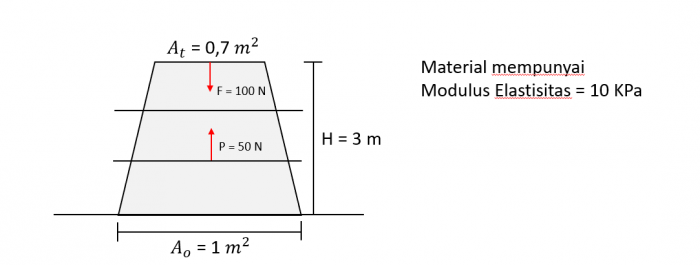
Dengan kode yang telah dibuat untuk menyelesaikan masalah pada sistem persamaan linear, kode tersebut juga dapat diaplikasikan pada simulasi Finite Element Analysis Contoh Soal

Seperti pada gambar diatas, suatu struktur diberikan gaya P keatas pada jarak 1 m dari lantai dan gaya F kebawah pada ujung struktur, hitunglah nodal displacement yang terjadi.

Penyelesaian

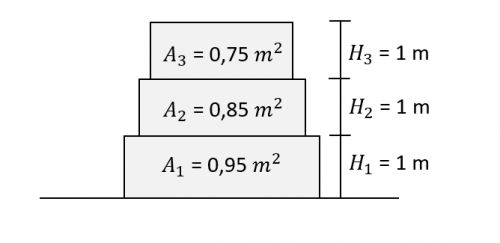
• untuk menyelesaikan masalah ini, kita dapat membagikan struktur tersebut menjadi 3 element dengan tinggi 1 meter dengan luas penampang rata-rata berturut-turut dari lantai 950 m2, 850 m2, dan 750 m2
• dengan rumus stiffness k = A*E/L kita dapat menghitung k1, k2, k3 berturut-turut 9500 N/m, 8500 N/m, dan 7500 N/m
• kemudian kita masukkan nilai-nilai stiffness k dan gaya F dan P beserta constraint yang ada ke matriks untuk penyelesaian

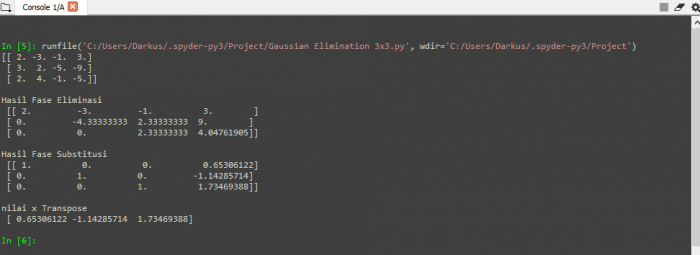
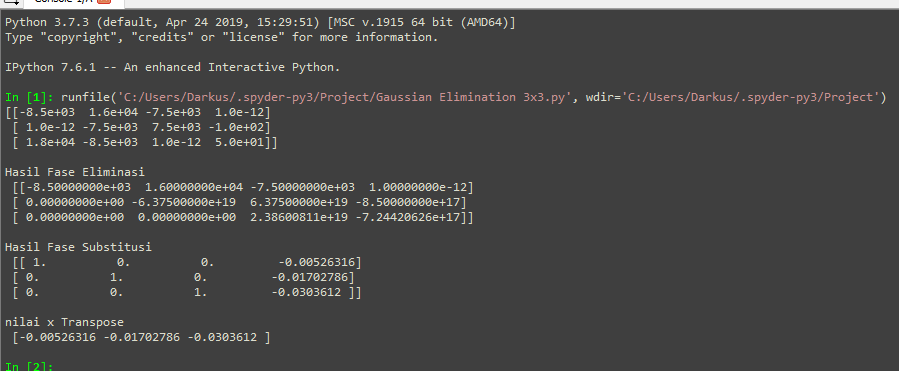
Penyelesaian yang didapatkan akan seperti berikut

dan didapatkan nodal displacement secara berturut-turut 0,00526 , 0,0170 , dan 0,030 kearah bawah

berikut adalah video penjelasan untuk tugas ini

Tugas metode Runge Kutta pada pegas

1. Persoalan dan analisis fisika

terdapat sebuah sistem pegas dan massa yang menempel pada dinding. Pegas tersebut memiliki konstanta sebesar 75 N/m dan Benda bermassa 2,5 kg. Gaya P yang diberikan pada sistem menjauhi dinding dengan besaran 10t apabila terjadi saat t<2s dan 20N apabila terjadi saat t>=2s. Terdapat juga persamaan untuk percepatan sistem yaitu y"= (P(t)/m)-((k/m)y). Disini kita harus mencari perpindahan maksimum sistem, dan diplotkan pada grafik perubahan posisi sistem terhadap waktu dimana sistem awal berada pada keadaan diam (v=0)

Analisis Fisika pada keadaan tersebut berlaku Hukum Newton ke-2 yaitu F=a.m, dimana a=percepatan benda dan m = massa benda. Selain itu berlaku juga hukum tentang gaya pegas, f=k.y, dimana k = konstanta pegas dan y = perubahan panjang pegas. Kedua gaya ini dapat memengaruhi perpindahan benda. Dikarenakan adany gaya tarik P dan gaya reaksi oleh pegas yang berlawanan dengan gaya tarik P atau dapat dirumuskan. Gaya total = gaya yang diberikan pada sistem - gaya reaksi pegas. m.y"=P(t)-ky dan apabila kedua ruas dibagi dengan massa maka persamaan akan menjadi y"=P(t)/m-(k/m)y

2. algoritma penyelesaian

terdapat pegas dengan konstanta 75 N/m. yang dihubungkan dengan benda bermassa 2,5 kg kemudian benda itu ditarik dengan gaya P(t). jika gaya ditarik kurang dari 2 detik maka gaya yang berlaku adalah 10t N. dan jika gaya ditarik lebih dari sama dengan 2 detik maka yang gaya yang berlaku 20 N. dengan gaya-gaya itu akan menghasilkan regangan. dan regangan terjauh dapat diselesaikan dengan metode runge kutta brdasarkan persamaan y"= (p(t)/m)-(k.y/m).